12. Как наследуются количественные признаки?

Количественные признаки - это все мерные признаки: рост (в сантиметрах), удой молока (в литрах), жирность молока (в процентах) и т. п. Анализ наследования количественных признаков значительно затруднен. Первое, с чем сталкивается генетик, - это непрерывный характер изменчивости.

Уже при анализе наследования окраски зерна у пшеницы, обусловленной полимерными генами, Н. Г. Нильсон-Эле установил непрерывный ряд изменчивости окраски зерна растений в F₂ от белой до интенсивно-красной. Число гетерозиготных локусов, отвечающих за данный признак, можно было установить по количеству появившихся рецессивных потомков: 1/16 белозерных - расщепление идет по двум локусам, 1/64 - по трем, 1/256 - по четырем, 1/1024 - по пяти и т. д., т. е. 1/4ⁿ. Таким образом можно выявить только число локусов, по которым родители различаются.

Число пар факторов n, отвечающих за исследуемый признак, вычисляется по формуле

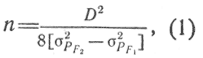
где D - разница между средними арифметическими признаков у родителей; σP_F1, σP_F2 - фенотипическая изменчивость F₁ и F₂ соответственно.

Наследование количественных признаков подчиняется менделевским законам расщепления: чем больше пар аллелей влияет на признак, тем больше варьирование по данному признаку. Гибриды в F₁ в отношении количественных признаков оказываются промежуточными между родительскими формами, в F₂ наблюдается варьирование признака от наименьшего значения одного родителя до наибольшего значения другого.

В F₂ количество генотипов равно 3ⁿ, но генетических значений меньше, так как они зависят только от количества доминантных аллелей, а не от их локализации. Например, если признак контролируется двумя парами факторов, в F₂ будет 3² = 9 генотипов. Однако формы А₁А₁а₂а₂, a₁a₁A₂A₂ и А₁а₁А₂а₂ имеют одинаковое генетическое значение, так как включают по две доминанты. Это касается и форм с одной и тремя доминантами. В нашем примере генетических значений пять: 4А, 3A, 2А, 1А, 0А, т. е. 2n + 1.

Распределение потомства соответствует биномиальной кривой, а коэффициенты генетических значений - показателям степени членов разложения бинома Ньютона:

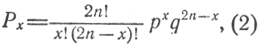
где Р_х - вероятность числа особей определенного генетического значения; 2n - число аллелей, контролирующих исследуемый признак; х - число доминантных аллелей определенного генетического значения; р - вероятность доминантного аллеля в популяции; q - вероятность рецессивного аллеля в популяции; ! - факториал (произведение натурального ряда чисел от большего до самого малого, например 5! равно 5·4·3·2·1).

Если х = 0 или х = 2n, формула (2) упрощается:

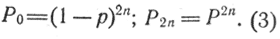
Практически вычисления можно сократить: частота особей определенного генетического значения равна частному от деления произведения частоты предыдущего члена и его генетического значения на число предшествующих членов:

число доминантных генов 
в генотипе:              4А     3А     2А     1А     0А 
частота генотипов:      1/16   4/16   6/16   4/16   1/16

Имеются и другие способы подсчета расщепления по количественным признакам.

Кроме генетических свойств организма существует ряд внешних по отношению к нему воздействий, которые могут сглаживать наследственные различия и еще более способствовать непрерывному характеру изменчивости этих признаков. Общая фенотипическая изменчивость σ_Р² слагается из двух факторов: генотипической изменчивости σ_G² и изменчивости под влиянием окружающей среды σ_E²:

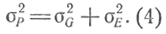
Значение σ_G² найдем следующим образом. Изменчивость в F₁ определяется лишь условиями окружающей среды, так как особи в F₁ по генотипу однородны, т. е. σ²_F1 = σ²_E; изменчивость в F₂ определяется двумя факторами, т. е. σ²_F2 = σ²_G + σ²_Е. Подставляя вместо σ²_Е его значение в формулу (4), найдем

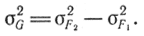
Величину σ²_Е можно найти с помощью метода идентичных однояйцевых близнецов. Все наблюдаемые у них различия определяются влиянием условий окружающей среды, т. е. σ²_Р = σ²_Е.