6. Если полученные результаты эксперимента отличаются от теоретически ожидаемых, то как можно установить, что полученное отклонение случайно?

Расщепление потомства в F₂ обычно не совпадает с теоретически ожидаемым, так как в любом эксперименте анализируется не идеальная популяция, а лишь большая или меньшая выборка, в которой неизбежны случайные отклонения (ошибки выборки). Какие расхождения между фактически полученными и теоретически ожидаемыми результатами можно допустить, чтобы они не были следствием действия каких-либо факторов, нарушающих расщепление, а были случайными и обусловливались, например, недостаточной величиной выборки? В статистике принято считать, что если отклонение встречается чаще, чем одно на 20 проб (¹/₂₀ = 0,05), то оно не случайно.

Для статистической оценки отклонения применяют метод χ² (хи-квадрат), который позволяет определить вероятность совпадения полученных результатов с теоретически ожидаемыми (табл. 1):

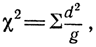
где d² - квадрат отклонения полученных результатов от ожидаемых; g - ожидаемые величины.

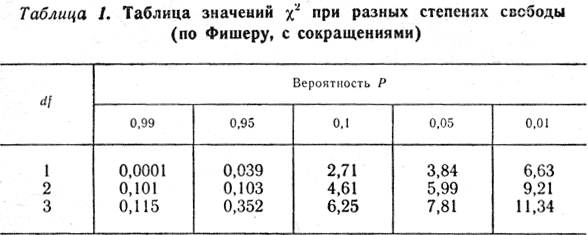
Таблица 1. Таблица значений χ² при разных степенях свободы (по Фишеру, с сокращениями)

Например, при моногибридном скрещивании получено потомство из 400 особей. Ожидаемое расщепление должно быть 3/4 А-:1/4 аа, т. е. 300 особей одного фенотипа и 100 особей другого. В опыте наблюдалось 285 особей одного и 115 особей другого фенотипа (табл. 2). Для того чтобы определить, случайно ли полученное отклонение, найдем λ²:λ² = 0,75 + 2,25 = 3,0. Согласно правилам статистики число степеней свободы (d, f) на единицу меньше, чем число классов (п - 1), т. е. в нашем примере d, f = 1 (см. табл. 1). В строке таблицы, соответствующей числу степени свободы, равной 1, найдем значение λ², равное 3,84, что соответствует вероятности Р ≈ 0,05. Таким образом, полученное в данном опыте отклонение от ожидаемого расщепления можно считать случайным.

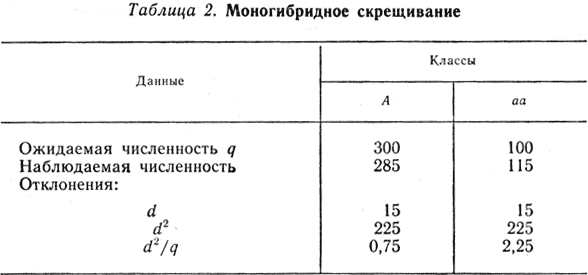
Таблица 2. Моногибридное скрещивание