
Приложение 4
Мультифакториалыюе наследование и главные гены
Анализ сегрегационных отношений в их непосредственном выражении возможен в случае качественно различимых фенотипов (разд. 3.6.1.3), поскольку в этом случае простой менделевский тип наследования можно предположить и обосновать четко распознаваемыми фенотипами. Однако для многих признаков человека такой анализ еще невозможен. Их наследование необходимо моделировать с помощью биометрического анализа количественных признаков (разд. 3.6.1.4). К ним относятся такие нормальные признаки, как рост и IQ, а также физиологические и биохимические характеристики, такие, как уровень холестерина в сыворотке. В эту же категорию признаков включают большинство широко распространенных болезней. Некоторые подходы к анализу количественных признаков описаны в разд. 3.6.1. Было дано обоснование концепции наследуемости и предложены стратегии пошагового анализа в соответствии с моделью мультифакториального наследования с пороговым проявлением или без такового. Среди этих стратегий мы обсуждали поиск фенотипических подклассов, а также анализ физиологических маркеров или ассоциаций с различными системами генетического полиморфизма.
В последние годы несколько авторов предложили статистические методы более строгого тестирования мультифакториальной модели против моногенной и идентификации эффектов главных генов на мультифакториальном фоне [139; 140; 646; 647]. В общем случае эти методы включают два этапа. Сначала формулируются предположения относительно типа наследования изучаемого признака, а затем на основе этих предположений рассчитываются частота (для альтернативно распределенных признаков) или распределение (для непрерывно распределенных признаков) в конкретных группах родственников. Так создается предварительная "модель" конкретного типа наследования. Потом с помощью статистических методов проверяется соответствие выборки эмпирических данных и значений, получаемых на основе построенной модели. Следовательно, этот подход к анализу принципиально не отличается от описанных в разд. 3.3.3 и 3.3.4 для тестирования соответствия семейных данных простому менделевскому типу наследования. Иногда формулируют несколько альтернативных моделей, а затем сравнивают их с реальными данными.
Модели нельзя сконструировать без упрощающих допущений. Это неизбежно и не влечет серьезных последствий при условии, что все допущения четко сформулированы. Важно понимать, что, если набор данных соответствует ожидаемым значениям, вытекающим из определенной модели, это еще не доказывает, что построенная модель адекватно описывает реальную ситуацию. Должны быть исключены все другие возможные модели. Очень часто такое исключение оказывается невозможным для моделей, типичных в генетике человека, например, когда мультифакториальное наследование тестируется против аутосомно-доминантного наследования с неполной пенетрантностью. Генетики, которые обычно работают с простыми менделевскими моделями, "избалованы": имеется лишь ограниченное число ситуаций, хорошо имитирующих моногенный тип наследования без дополнительных предположений. Как правило, в этих случаях они находятся на твердой основе надежных фактов. Однако при использовании мультифакториальных моделей дело обстоит иначе.
Ниже мы будем сравнивать две модели, которые имеют практическое значение для анализа генетической предрасположенности широко распространенных заболеваний: мультифакториальная модель с порогом и модель простого доминантного типа наследования с неполной пенетрантностью. Мы будем следовать в основном анализу, проведенному Крюгером [746], поскольку этот автор четко изложил предположения и упрощения модели. О некоторых других, сходных подходах мы упомянем лишь кратко (детальное обсуждение было проведено в разд. 3.6.2.2).
Простой диаллельный тип наследования с неполной пенетрантностью. Пусть пенетрантности генотипов АА и Аа будут w1 и w2 соответственно, а индивиды с генотипом аа всегда здоровы. Тогда частота признака в популяции равна
Р = p2w1 + 2pqw2 = р2(w1 - 2w2) + 2pw2
(p - частота аллеля А). Реалистическим упрощением этой модели для практических ситуаций будет предположение w1 = 1 (полная пенетрантность гомозигот АА).
Мультифакториальное наследование с пороговым эффектом. Обозначим через х фенотипическое значение подверженности заболеванию [654]. Это значение можно разбить на две компоненты, как показано в разд. 3.6.1. Предполагается, что средовое значение Е не коррелирует с генотипическим значением G:
Vx = VG + VE
и что генотипическое значение не содержит эпистатическую компоненту. G представляет собой сумму вкладов независимо действующих генов, и его распределение в популяции стремится к нормальному при увеличении их числа. Логично предположить, что G нормально распределено в популяции и что средовое отклонение Е имеет нормальное распределение. При этих условиях фенотипическое значение х также будет распределено нормально.
Поскольку подверженность является гипотетической переменной, ее можно определить так, чтобы х, G и Е имели среднюю О, а фенотипическое значение х имело дисперсию 1. Тогда порог однозначно определяется популяционной частотой Р, как та точка, которая делит стандартизованное нормальное распределение (нормальное распределение со средней 0 и дисперсией 1) на две части с частотами 1 - Р и Р. Рассмотрим двух родственников определенной степени родства, выбранных из популяции случайным образом. Пара их подверженностей (x1, x2) является случайной величиной, которая имеет двумерное нормальное распределение. Когда задан коэффициент корреляции двух подверженностей rx1,x2, это распределение полностью определено, и можно вычислить вероятность того, что какой-то один или оба родственника поражены. При описанных выше условиях коэффициенты фенотипической, генотипической и средовой корреляций подверженностей двух родственников связаны соотношением [488]:
rх1х2 = rG1G2H2 + rЕ1Е2Е2,
где Н2 = VG/VX = VG - наследуемость (в широком смысле) и Е2 = 1 - Н2 = VE. В большинстве случаев корреляцию между средовыми компонентами E1 и Е2 двух родственников нельзя определить, поэтому предположим, что она равна 0. Кроме того, будет исследоваться только специальный случай H2 = h2 (т. е. VG = VA) в соответствии с опытом количественной генетики, согласно которому неаддитивная компонента Н2 - h2 обычно очень мала. Тогда справедливо следующее уравнение:
rx1x2 = rh2,
где r = rG1G2 имеет фиксированное значение, зависящее только от типа родства, а модель зависит только от параметров h2 и Р. Дополнительное рассмотрение средовой компоненты Е (что эквивалентно h2 < 1) опровергает нереалистическое предположение о четком пороге. Он заменяется "пороговой областью", ширина которой задается с помощью VE. Предполагают, что внутри этой пороговой области вероятность проявления заболевания непрерывно увеличивается от 0 до 1.
Сравнение моногенной и мультифакториальной моделей. Ниже мы сравним эти модели для ряда значений популяционной частоты Р, для ряда значений пенетрантностей w в диаллельной модели и для различных предположений, касающихся h2, в мультифакториальной модели. Для диаллельной модели вычисление проводят непосредственно, когда предполагается, что регистрация проводилась в соответствии с единичным отбором (разд. 3.3). В случае мультифакториальной модели r = h2/2 для родителей, сибсов и детей, r = h2 для монозиготных близнецов. Исходя из этого и используя двумерное нормальное распределение подверженностей двух родственников I1 и I2, можно получить условную вероятность Q того, что I2 поражен, если поражен I1. Q равно отношению вероятности того, что оба родственника поражены, к вероятности Р1, что поражен I1. Q соответствует темно-серой области под поверхностью плотности нормального распределения на рис. П.4.1, тогда как области, имеющие светло-серый цвет, соответствуют вероятностям событий: I1 поражен, I2 нормальный и I1 нормальный, I2 поражен. На рис. П.4.1, А представлен случай двух неродственных индивидов. Риск каждого из них не зависит от риска другого: Q = Р. Это находит свое отражение в центральной симметрии поверхности плотности распределения. На рис. П.4.1, Б показано совместное распределение подверженностей для родственников первой степени родства. В этом случае предполагается, что h2 = 1 (и таким образом r = 1/2). Следствием этого является тот факт, что поражение I1 увеличивает риск быть пораженным для родственника I2:Q > Р. Объемы закрашенных участков под поверхностью плотности распределения можно вычислить с помощью численного интегрирования, на чем подробно мы останавливаться не будем (тетрахорические функции Пирсона, которые используются некоторыми авторами, обладают недостатками. Обсуждение этой проблемы см. в [746]).
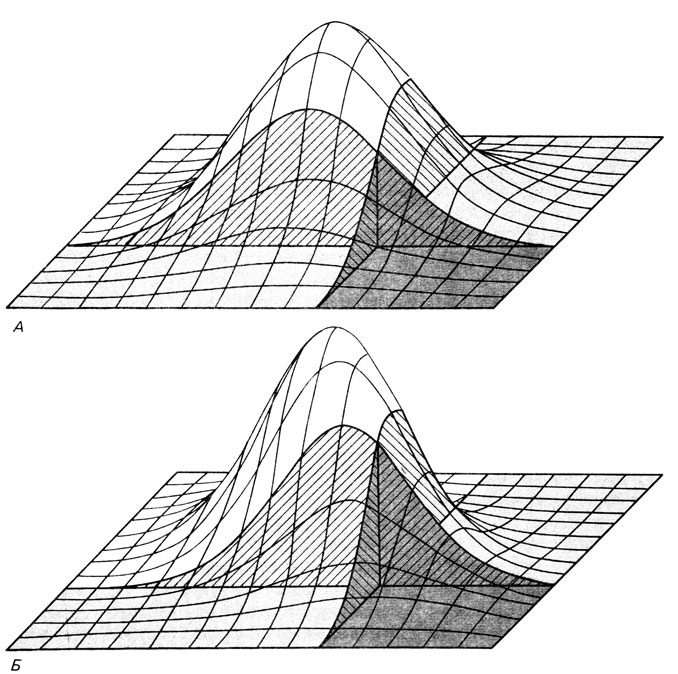
Рис. П.4.1. Поверхность двумерного нормального распределения подверженностей заболеванию двух индивидов. Два порога обозначены штриховыми плоскостями. Темные закрашенные области в переднем правом углу указывают вероятность Q того, что оба индивида поражены. А. Два неродственных индивида в панмиксной популяции. Б. Два родственника первой степени родства. Интенсивно окрашенная область намного больше, чем на А, что указывает на возрастание риска для родственника быть пораженным, если пробанд страдает тем же заболеванием
На рис. П.4.2 и ПАЗ приведены результаты сравнения моделей. Используются следующие обозначения: Q1 - частота признака у детей или родителей пробандов, Q2 - частота среди сибсов или дизиготных близнецов пробандов, Q3 - частота среди монозиготных близнецов пробандов, Q1,1 - частота среди сибсов пробандов с двумя здоровыми родителями, Q2,1 - частота среди сибсов пробандов, один из родителей которых поражен, Q2,2 - частота среди сибсов пробандов, оба родителя которых поражены.
![Рис. П.4.2. Частота признака среди детей (или родителей) пробандов (Q1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000156.jpg)
Рис. П.4.2. Частота признака среди детей (или родителей) пробандов (Q1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
![Рис. П.4.3. Частота признака среди сибсов пробандов (Q2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000157.jpg)
Рис. П.4.3. Частота признака среди сибсов пробандов (Q2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
Диаграммы на рис. П.4.2 и П.4.3 очень просты. Они демонстрируют частоты в двух моделях для детей (или родителей) и для сибсов безотносительно к типам брака родителей. Кривые обнаруживают определенное перекрывание для высокой частоты Р (частота = 0,2-0,5% и выше) между доминантным наследованием с низкой пенетрантностью и мультифакториальным наследованием с высокой наследуемостью. С другой стороны, разделение двух моделей наследования признака с низкой частотой очень хорошее. Для монозиготных близнецов (на рисунке не показано) мультифакториальная модель всюду может имитировать поведение диаллельной модели. Однако противоположное, т. е. имитирование поведения мультифакториальной модели с помощью диаллельной, возможно только при высоких значениях h2, но не при низких.
Следовательно, имитирование возможно не только раздельно для монозиготных и дизиготных близнецов, но и одновременно на обеих выборках. Для исследования этой проблемы изучалось отношение
| R1 = | Q3 | |
| Q2 |
частот среди МЗ и ДЗ близнецов (рис. П.4.4). И в этом случае не всякая мультифакториальная модель имитируется, но модели с высокими наследуемостями можно дифференцировать от моногенной модели. Для последней верхний предел R1 (для разных значений пенетрантностей) монотонно стремится к 4, когда популяционная частота приближается к 0 (и практически равен 4 для Р ≤ 0,01%). Это подтверждает близнецовый критерий Пенроуза [837]: если конкордантность монозиготных близнецов более чем в четыре раза превышает конкордантность дизиготных близнецов, то однолокусную модель можно исключить в пользу мультифакториальной. С другой стороны, значение R1 < 4 не исключает мультифакториальную модель.
![Рис. П.4.4. Частота признака среди монозиготных и дизиготных близнецов пробандов (R1 = Q3/Q2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000158.jpg)
Рис. П.4.4. Частота признака среди монозиготных и дизиготных близнецов пробандов (R1 = Q3/Q2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
На рис. П.4.5-П.4.7 показаны частоты Q1,1, Q2,1 и Q2,2 среди сибсов и родителей для типов брака непораженный × непораженный, пораженный × непораженный, пораженный × пораженный. В семьях с двумя непораженными родителями нет перекрывания в частотах Q1,1. Частоты для мульфакториального наследования даже с высокими наследуемостями ниже, чем при доминировании с неполной пенетрантностью, даже когда пенетрантность очень низка. С другой стороны, для Q2,1 (рис. П.4.6) имеется значительное перекрывание: в семьях с одним пораженным родителем мультифакториальную модель можно отличить от моногенной только при очень низкой наследуемости. Частота Q2,2 (тип брака плюс × плюс) обнаруживает принципиально те же цифры.
![Рис. П.4.5. Частота признака среди сибсов пробандов в браках здоровый х здоровый (Q1,1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000159.jpg)
Рис. П.4.5. Частота признака среди сибсов пробандов в браках здоровый × здоровый (Q1,1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
![Рис. П.4.6. Частота признака среди сибсов пробандов в браках пораженный х здоровый (Q2,1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000160.jpg)
Рис. П.4.6. Частота признака среди сибсов пробандов в браках пораженный × здоровый (Q2,1) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
![Рис. П.4.7. Частота признака среди сибсов пробандов в браках пораженный х пораженный (Q2,2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000161.jpg)
Рис. П.4.7. Частота признака среди сибсов пробандов в браках пораженный × пораженный (Q2,2) в диаллельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
До сих пор в анализе мы пренебрегали эффектами доминирования. Все исследования мультифакториальной модели были проведены в предположении h2 = H2. Однако было показано, что влияние эффектов доминирования принципиально сходно с влиянием средовых эффектов (т. е. понижение h2).
В общем, области всегда перекрываются. Учитывая тот факт, что мультифакториальная модель является абстракцией и что данные, обычно имеющиеся для такого анализа, подвержены выборочным ошибкам, эти результаты не следует считать вполне удовлетворительными. В качестве критерия, который бы лучше дискриминировал обсуждаемые модели, предлагалось отношение т. е. отношение ожидаемой частоты среди детей одного пораженного родителя (Q2,1) к ожидаемой частоте среди детей двух непораженных родителей (Q1,1). Но как показывает рис. П.4.8, для высокой частоты Р перекрывание все еще ощутимо, хотя для более низких Р разделение действительно намного лучше. Мультифакториальную модель можно отличить от моногенной, если R2 ≥ 2,5. Если частота среди сибсов пробандов в браке с одним пораженным родителем в 2,5 раза выше, чем среди сибсов с двумя непораженными родителями, то вряд ли следует считать адекватной диаллельную модель. Этот критерий можно сравнить с близнецовым критерием Пенроуза [837]: здесь, как и в ситуации с R2 < 2,5, также возможен неопределенный вывод, если R1 < 4. Интересно, что оба критерия, которые были установлены в основном на интуитивной основе, совместимы при анализе.
![Рис. П.4.8. Отношение частот среди сибсов пробандов в браках пораженный х здоровый и здоровый х здоровый (R2 = Q2,1/Q1,1) в диалдельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]](pic/000162.jpg)
Рис. П.4.8. Отношение частот среди сибсов пробандов в браках пораженный × здоровый и здоровый × здоровый (R2 = Q2,1/Q1,1) в диалдельной (штриховые линии) и мультифакториальной (сплошные линии) моделях [746]
Важным параметром является наследуемость h2. Ее следует оценить прежде всего. На практике это можно сделать двумя независимыми способами: используя уровни конкордантности МЗ близнецов или сравнивая частоту Q среди родственников пробандов с популяционной частотой Р. Первый метод дает H2, а не h2, но можно надеяться, что разность незначительна. Этот аспект обсуждается в разд. 3.8 и приложении 6. Второй метод зависит от свойств мультифакториальной модели, которые не всегда реалистичны и контролируемы.
Фолконер [654; 655] предложил принцип, который формально аналогичен проведению селекционного эксперимента в количественной генетике. Пусть G будет средней подверженностью в популяции, А - средней подверженностью пораженных, R - средней подверженностью родственников (данной степени родства) пораженных. Тогда отношение разностей R-G ("ответ") и A-G ("селекционный дифференциал") равно коэффициенту регрессии b подверженности родственников на подверженность пробандов
| b = | R - G | . |
| A - G |
При указанных выше предположениях о подверженности (нормальное распределение со средней 0 и дисперсией 1) левая часть равна коэффициенту корреляции подверженностей
b = r = h2,
совпадающему с коэффициентом родства (например, b = 1/2 для родственников первой степени родства). Знаменатель правой части можно вычислить из (стандартного) нормального распределения, используя расстояние между популяционной средней и пороговым значением, соответствующим популяционной частоте Р признака. Фолконер предложил получать значение числителя как разность между пороговым значением, соответствующим частоте Q признака среди родственников, и пороговым значением для популяции. Улучшенная номограмма (рис. П.4.9) с коэффициентом корреляции г подверженностей пробанда и родственника вместо h2 была опубликована Смитом [880]. Эта номограмма охватывает также отрицательные значения h2 (ниже и справа от нулевой линии на рис. П.4.9). Отрицательные значения биологически бессмысленны, но, будучи следствием малого объема выборки, могут использоваться в случае объединения нескольких выборок для получения обобщенной оценки.
![Рис. П.4.9. Таблица для получения оценки h2 из частоты (в %) признака в общей популяции и среди родственников пробандов первой степени родства. Например, если частота заболевания составляет 0,2% в общей популяции и 4% среди детей пробандов, то это соответствует коэффициенту корреляции r = 0,40, и поскольку h2 = 2 х r, то наследуемость h2 = 0,8. Обычно применяется формула h2 = r/R. Здесь R - мера родства, которую можно получить из формул для h2 в разд. 3.6.1.5. Например, R = 1/2 для родственников первой степени родства, R = 1/4 для родственников второй степени родства и R = 1 для МЗ близнецов [875а]](pic/000163.jpg)
Рис. П.4.9. Таблица для получения оценки h2 из частоты (в %) признака в общей популяции и среди родственников пробандов первой степени родства. Например, если частота заболевания составляет 0,2% в общей популяции и 4% среди детей пробандов, то это соответствует коэффициенту корреляции r = 0,40, и поскольку h2 = 2 × r, то наследуемость h2 = 0,8. Обычно применяется формула h2 = r/R. Здесь R - мера родства, которую можно получить из формул для h2 в разд. 3.6.1.5. Например, R = 1/2 для родственников первой степени родства, R = 1/4 для родственников второй степени родства и R = 1 для МЗ близнецов [875а]
Сравнение значений, ожидаемых на основе этих моделей, с наборами реальных данных. Номограммы на рис. П.4.1-П.4.8 можно использовать для сравнения реальных семейных и близнецовых данных с ожидаемыми на основе двух моделей. Часто такое оценивание несет на себе интуитивный отпечаток того, какая модель рассматривается априори как более близкая к истине. Заметим, что сравнения неэффективны, если проводятся раздельно для родственников разных степеней родства: даже если каждое из них не позволяет отвергнуть какую-либо одну из двух моделей, то на основании общей картины частот среди родственников разной степени родства иногда все же можно отдать предпочтение одной из альтернатив. Кроме того, до сих пор молчаливо предполагалось, что популяционная частота р известна. Однако это почти всегда не так: как правило, р нужно оценить из популяционной выборки. На практике оценивание p, которое необходимо для определения величины h2, например используя табл. П.4.9, часто бывает нелегкой проблемой. Если можно, то оценки р должны быть получены для тех же популяций, в которых регистрируются семьи для анализа, поскольку многие мультифакториальные признаки, такие, как врожденные пороки или широко распространенные заболевания, обнаруживают сильную межпопуляционную вариабельность.
Метод, позволяющий сравнивать общую картину наблюдаемых частот с модельными, основывается на принципе максимального правдоподобия. Мы опишем его, сравнивая две обсуждаемые нами модели. Частоты изучаемого признака для разных категорий родственников пробандов назовем Q1, Q2, Q3 ..., QU (в нашем случае u = 6). Для каждой частоты Qi (i = 1, ..., u) имеется реальное значение Qi = ki/ni, определяемое из выборки ni родственников определенной степени родства, ki из которых поражены изучаемым заболеванием. Кроме того, из исследования популяционной выборки n0 индивидов может быть известно наблюдаемое значение частоты в общей популяции Q0 = k0/n0 для оценивания Р. Если предположить, что выборки для определения Qi содержат для каждого пробанда только одного родственника определенной степени родства, то вероятность всех этих наблюдаемых значений вместе дается формулой
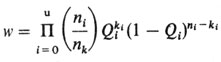
Здесь Qi обозначает (неизвестное) ожидаемое значение "реальной" частоты в i-й категории родственников. Возвращаясь к двум описанным выше моделям, можно сказать, что Qi представляет собой функцию параметров либо простой доминантной модели с неполной пенетрантностью, либо мультифакториальной модели с порогом (параметры: τ1 = Р, τ2 = w - пенетрантность в однолокусной модели; τ1 = Р, τ2 = h2 - в мультифакториальной модели). В этом случае уравнение становится функцией правдоподобия наблюдаемых значений Q1, ..., Qu в соответствии с гипотезой, что эмпирически найденные частоты среди различных категорий родственников определяются типом наследования, предполагаемым в одной из этих двух моделей. Для каждой из них вычисляют два значения параметров τ1 и τ2, для которых функция правдоподобия максимальна. Обозначим эти оценки максимального правдоподобия (МП-оценки) параметров τ1 и τ2 через τ1ˆ и τ1ˆ, а Qiˆ = Qi (τ1ˆ, τ2ˆ) будут соответствующими МП-оценками Qi(Q0ˆ = τ1ˆ). Эти оценки лучшие в рамках конкретной модели. Теперь их нужно сравнить с действительно наблюдаемыми частотами. Точность, с которой модель описывает наблюдения, можно тестировать с помощью выражения
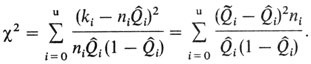
Когда справедлива нулевая гипотеза, т. е. когда распределение частот среди различных категорий родственников соответствует предполагаемому типу наследования, это выражение распределено приближенно как χ2 с u - 1 степенью свободы. Следовательно, если найденное значение выражения (П.4.2) больше табличного значения χ2, то нулевая гипотеза отвергается. Когда таким способом тестируются обе модели, то возможны четыре исхода:
1) нет различия между эмпирическими данными и какой-либо моделью: никакую модель нельзя исключить;
2) можно исключить только моногенную модель;
3) можно исключить только мультифакториальную модель;
4) исключаются обе модели. Необходимо помнить, что даже альтернативы 2 и 3 не доказывают справедливость какой-либо одной из двух моделей. Одинаково хорошо эти данные можно объяснить многими другими моделями. На практике часто используется выражение
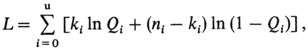
которое равно (за исключением дополнительной константы, не зависящей от параметров модели) натуральному логарифму выражения в уравнении П.4.1. Кроме уравнения П.4.2 для тестирования вполне пригодна формула
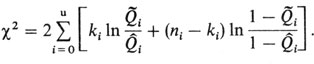
Мы не станем здесь описывать методы вычисления (они стандартны для математиков [746; 804]) МП-оценок параметров τ1ˆ и τ2ˆ, т. е. тех значений параметров, для которых функция логарифма правдоподобия (уравнение П.4.3) принимает максимальное значение.
Как мы поступаем на практике? Анализ широко распространенного заболевания - дело непростое и обычно требует помощи со стороны специалиста по статистической генетике. Иногда бывает трудно констатировать простые менделевские типы наследования из-за высокой частоты признака и сниженной пенетрантности. Однако даже искушенный специалист часто оказывается не в состоянии отличить моногенный признак с низкой пенетрантностью от мультифакториального признака.
Существенное значение имеет тщательный анализ гетерогенности. В этой группе широко распространенных признаков за диагнозом одной болезни часто могут скрываться несколько заболеваний с разными генетическими и негенетическими причинами. Кроме того, часто имеет место генотип-средовое взаимодействие, которое трудно оценить. Передачу признака в очень большой моногенной родословной можно легко разъяснить генетически, но результаты, полученные для этой группы родственников, могут оказаться неприменимыми к другим индивидам и их семьям. Прежде чем проводить генетический анализ, необходимо стандартизовать данные по возрасту начала, полу и другим факторам. Как правило, наиболее эффективным оказывается сравнение данных исследователя с различными генетическими моделями. Для большого числа моделей разработаны компьютерные программы. С их помощью можно определить соответствие реальных данных тому или иному типу наследования. Среди наиболее распространенных моделей - простое доминантное наследование, рецессивное наследование, полигенное наследование, полигенное наследование в комбинации с главным геном, негенетическая семейная агрегация. Однако даже при столь "исчерпывающей" обработке данных необходимо проявлять осторожность и не спешить с окончательными выводами. Иногда незначительные изменения данных существенно их меняют. Вот почему надо с опаской относиться к принятию модели одного гена на основе такого анализа. С другой стороны, неудача при поиске моногенного наследования не обязательно означает, что нет главного гена. Важно, чтобы исследователь был осведомлен о биологическом, биохимическом и патофизиологическом фоне изучаемого заболевания. Применение новейших методов лабораторных исследований дает возможность выявить гетерогенность и приблизиться в познании конкретной патологии к генному уровню. Это намного более эффективно, чем использовать "фенотипические" диагнозы, которые на самом деле скрывают гетерогенность. Конечно, для многих болезней мы в настоящий момент можем удовольствоваться только этим. В общем случае наше проникновение в суть генетического механизма передачи таких болезней (например, шизофрении) будет полным, хотя на основе других факторов мы можем быть убеждены, что ключевую роль в их этиологии играют именно генетические факторы. Во всех случаях необходимы совместные усилия генетиков, статистиков и специалистов по изучаемой болезни.
Тестирование различных генетических моделей было проведено для ряда широко распространенных патологий, таких, как эпилепсия [611, 793], катехол-О-метил-трансферазная активность эритроцитов [666], гиперхолестеринемия [794], коронарная болезнь сердца [847] и гиперлипидемия [954]. Некоторые обобщения можно найти в [819-822].
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'