
Приложение 6
Вычисление коэффициента наследуемости по близнецовым данным
Понятие наследуемости было введено в разд. 3.6.1.5 и разд. 3.6.2. Там же описаны методы получения оценок наследуемости пороговых признаков. Критерием служило отношение между частотой среди близких родственников пробандов и в общей популяции. Для непрерывно распределенных признаков, таких, как рост, наследуемость оценивали из сравнения родителей и детей. В качестве альтернативного способа получения оценок наследуемости можно использовать близнецовые данные. В разд. 3.6.1.5 наследуемость была определена как
| h2 = | VA | , |
| VP |
т. е. отношение аддитивной генетической дисперсии (VA) к общей фенотипической дисперсии (VP). Отмечалось также, что в генетике человека h2 часто называется "наследуемостью в узком смысле" в противоположность Н2 = VG/VP (наследуемость в широком смысле, называемая также степенью генетической детерминации), где VG - общая генотипическая дисперсия, включающая доминирование, эпистаз и дисперсию взаимодействия.
В этом приложении получение оценок наследуемости h2 будет ограничено близнецовыми данными. Из одних лишь близнецовых данных невозможно оценить VD, дисперсию доминирования. Кроме того, по данным Фолконера VD обычно незначима по сравнению с VA [63]. Таким образом, ошибка, вытекающая из предположения о совпадении общей генотипической дисперсии (VG) и аддитивной дисперсии (VA), по-видимому, мала. Если сделать предположение о VG = VA, формула примет вид
| h2 = | VG | . (П.6.1) |
| VP |
Как показано в разд. 3.6.1,
VP = VA + VD + VE + VI + VM + CovGE.
Здесь VE - средовая дисперсия, VI - дисперсия вследствие взаимодействия наследственности и среды и VM - дисперсия измерений одного и того же признака, отражающая либо истинно разные значения (такие, как давление крови в разные дни), либо ошибки измерений. CovGE - ковариация между генетической и средовой компонентами фенотипического значения. Получение оценки наследуемости из близнецовых данных требует, чтобы VI и CovGE были равны 0. Это предположение в большинстве случаев нереалистично, особенно в генетике поведения, но если параметры VI и CovGE отличаются от нуля, получение их оценок представляет собой невероятно трудную задачу. Следует учитывать дисперсию измерений VM, хотя во многих близнецовых исследованиях ее не рассматривают. Уравнение П.6.1 принимает вид
| h2 = | VG | . |
| VG + VE + VM |
Биологический смысл имеет и альтернативное определение
| h'2 = | VG | . |
| VG + VE |
Здесь рассматривается только постоянная часть фенотипической дисперсии, а не та, которая изменяется ото дня ко дню.
Если CovGE = О, то справедливо следующее соотношение между коэффициентом корреляции rp1p2 фенотипических значений Р1 и Р2 двух родственников, коэффициентом корреляции rG1G2 генотипических значений G1 и G2 и коэффициентом корреляции RЕ1Е2 средовых значений Е1 и Е2:
rР1Р2 = rG1G2h2 + rE1E2E2,
где
| E2 = | VE | . |
| VP |
Коэффициенты корреляции можно определить как внутрипарные корреляции, если два родственника являются близнецами:
rР,МЗ = h2 + RЕ,МЗЕ2 для МЗ близнецов, (П.6.2)
rР,ДЗ = rG,ДЗh2 + rЕ,ДЗЕ2 для ДЗ близнецов, (П.6.3)
Здесь используется теоретическая генотипическая корреляция rG,МЗ, которая равна 1 для МЗ близнецов (разд. 3.6.1.5).
Если предположить, что средовая корреляция между близнецами МЗ совпадает со средовой корреляцией между близнецами ДЗ пар, то
| h2 = | rP,МЗ - rP,ДЗ | . (П.6.4) |
| 1 - rG,ДЗ |
Это выражение известно как индекс Н (Хольцингера). Коэффициент фенотипической внутрипарной корреляции равен
| rР,близнецы = | VPB | , |
| VPB + VPW |
где VPB - фенотипическая дисперсия между парами и VPW - фенотипическая дисперсия внутри пар.
Компоненты дисперсии VPB и VPW можно оценить из фенотипических значений рi1, pi2 (i = 1, 2, ..., n), наблюдаемых в n парах:
VPW - DQW,
VPB = (DQB - DQW)/2. (П.6.5)
Здесь DQW и DQB - внутрипарные и межпарные средние квадраты
DQW = 1/2n ∑i=1n(pi1 - pi2)2, (П.6.6)
DQB = 2/n-1 ∑i=1n(pi.‾ - p..‾)2, (П.6.7)
где
р‾i. = pi1+pi2 / 2 = среднее фенотипическое значение i-й пары,
р‾.. = 1/n ∑i=1n p‾i. = общая средняя всех измерений в близнецовой выборке.
Для расчетов вместо уравнения П.6.7 можно использовать
DQB = 1/2(n-1) [∑i=1nyi2 - 1/n (∑i=1nyi)2], (П.6.7')
где yi = рi1 + pi2 (i = 1, 2, ..., n).
Компоненту дисперсии VPW можно разложить следующим образом:
VPW = VG(1 - rG,близнецы) + VE(1 - rЕ,близнецы) + VМ. (П.6.8)
Это уравнение применимо к МЗ парам, ДЗ парам или неродственным контрольным парам из общей популяции (СР):
VPW(МЗ) =VE(1 - rE,МЗ) + VM, (П.6.9)
VPW(ДЗ) = VG(1 - rG,ДЗ) + VE(1 - rЕ,ДЗ) + VM, (П.6.10)
VPW(СР) = VG + VE + VP = VM. (П.6.11)
Наш дальнейший анализ будет состоять из двух этапов. На первом из них нужно исследовать, отклоняется ли h2 значимо от нуля. Затем нужно оценить h2.
Тестирование нулевой гипотезы (h2 = 0). Если предположить, что rЕ,МЗ = rЕ,ДЗ, то из уравнений П.6.2 и П.6.3 следует, что гипотеза h2 = 0 эквивалентна гипотезе
rР,МЗ = rP,ДЗ.
Для тестирования этой последней гипотезы используется тот факт, что в данном случае
z = 1/2 ln 1+rP,M3/1-rP,M3 - 1/2 ln 1+rP,ДЗ/1-rP,ДЗ
и имеет приблизительно нормальное распределение со средней 0 и дисперсией
| 1 | + | 1 |
| nМЗ - 3/2 | nДЗ - 3/2 |
Здесь rˆP,МЗ и rˆP,ДЗ - оценки rP,МЗ и rP,ДЗ, полученные из nМЗ МЗ пар и nДЗ ДЗ пар.
Получение оценок h2 (u h'2).
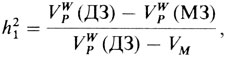
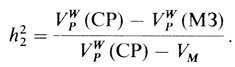
Чтобы оценить h2 (или h'2), внутрипарные дисперсии заменяются их оценками из дисперсионного анализа. Точной формулы стандартной ошибки этих двух оценок h2 нет. Если VM можно пренебречь по сравнению с VPW, то приближенно справедлива следующая формула:
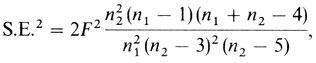
где F означает наблюдаемое значение отношения VPW(MЗ)/VPW(ДЗ) или VPW(MЗ)/VPW(СР) соответственно, n1 и n2 - количество пар, по которым оцениваются дисперсии числителя и знаменателя. Следует учесть, что помимо выборочных ошибок оценки в уравнениях П.6.12 и П.6.13 смещены.
Уравнение П.6.12: если предполагается, что средовые корреляции между МЗ и ДЗ идентичны, т. е. rE,МЗ = rЕ,ДЗ, то из уравнений П.6.9 и П.6.10 вытекает, что
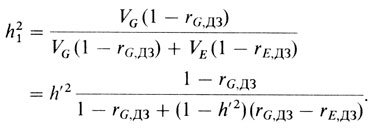
Следовательно, h12<> h1'2, если rЕ,ДЗ<> rG,ДЗ.
В силу этого h12 завышает h2, если rЕ,ДЗ > rG,ДЗ, потому что всегда h2 ≤ h'2. В других случаях предсказание смещения h12 при оценке h2 невозможно.
Уравнение П.6.13: из уравнений П.6.9 и П.6.10 вытекает, что
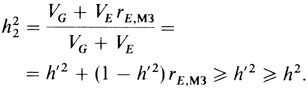
Здесь предполагается, что rЕ,МЗ ≥ 0. Следовательно, h22 будет обычно завышать h2.
В этих двух оценках h2 использовались исключительно внутрипарные дисперсии. Часто h2 оценивается также из коэффициентов внутрипарной корреляции, которые вычисляют с использованием дисперсии всей выборки МЗ и ДЗ близнецов, т. е. дисперсии между близнецовыми парами. Из уравнения П.6.4 можно получить следующую формулу для оценивания:
h32 = 2 (rР,МЗ - rP,ДЗ). (П.6.15)
Эта формула содержит предположение rG,ДЗ = 1/2, которое справедливо, только если брак панмиксный и нет ни доминирования, ни эпистаза. На практике это условие выполняется в лучшем случае приближенно. Кроме того, неизвестно rG,ДЗ > 1/2 или rG,ДЗ < 1/2. Следовательно, смещение в оценке h2 из уравнения П.6.15 нельзя предсказать.
Коррекция возможна, если rG,ДЗ > 1/2 вследствие ассортативного скрещивания и нет ни доминирования, ни эпистаза. Стандартную ошибку оценки h32 можно вычислить лишь очень приближенно
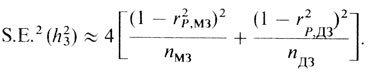
Замечания к изложенным методам получения оценки наследуемости. Из выше сказанного следует, что несмещенная оценка h2 по близнецовым данным невозможна, даже если пренебречь такими компонентами, как ковариация между наследственностью и средой (CovGE) и дисперсия взаимодействия (VI), и сделать маловероятное предположение об идентичности средовых корреляций rE,МЗ и rE,ДЗ, т. е. об идентичности общесредовых факторов для МЗ и ДЗ пар. И при таких сильно упрощающих предположениях остаются систематические ошибки, которые невозможно проконтролировать полностью.
Эмпирический способ преодоления этих трудностей заключается в вычислении альтернативных оценок из одних и тех же данных и в сравнении, насколько хорошо они совпадают. Три предложенные выше альтернативные оценки можно охарактеризовать следующим образом: h12 получается из классического сравнения МЗ и ДЗ близнецов. Смещение этой оценки включает генотипическую корреляцию между сибсами rG,ДЗ. Это значение равно 1/2 при панмиксных браках. Однако для многих признаков с известными оценками наследуемости (например, IQ или рост) показано, что браки в отношении их ассортативны. Направление и степень смещения зависят от разности генотипической и средовой корреляций между сибсами, которая обычно не известна. Следовательно, полезной может оказаться оценка наследуемости (h22), основанная на лицах контрольной выборки, хотя из-за зависимости от средовых корреляций rE,МЗ и rE,ДЗ она систематически завышает h2.
Дополнительное сравнение контрольных пар было предложено Фогелем и Вендтом в 1956 г. [926], но с тех пор никогда не использовалось. Аналогичная процедура теперь предложена Каминым (1974) [104]. Контрольные пары из близнецовых выборок легко могут быть подобраны по возрасту и полу (тем самым исключаются компоненты дисперсии, содержащиеся в большинстве близнецовых выборок).
Эта "досадная" дисперсия служит основным аргументом против использования оценки, получаемой из коэффициентов внутриклассовой корреляции (h32), которая содержит указанные компоненты дисперсии, если близнецовые выборки недостаточно гомогенны (как в случае выборки военнослужащих). Эта проблема разбирается в разд. 8.2.1.3.
Наследуемость IQ в качестве примера. Близнецовая выборка состояла из 50 близнецовых пар немцев мужского пола в возрасте от 23 до 30 лет; 25 МЗ и 25 ДЗ пар. Все близнецы были военнослужащими, и поэтому их выборку можно считать несмещенной относительно общественно-экономического статуса и образования. Интеллектуальное развитие оценивали по суммарному показателю Амфайера с поправкой на возраст [2234]; этот показатель пропорционален IQ. Для составления группы контрольных пар с наименьшими внутрипарными возрастными различиями использовали следующую процедуру. Все близнецовые пары независимо от зиготности классифицировали по возрасту (от меньшего к большему). Затем первую и вторую, третью и четвертую пары и т. д. объединяли в четверки, из которых путем случайного обмена соблизнецами формировали новые пары. Наблюдаемые значения показателя интеллектуального развития (рi1, pi2), а также полученные на их основе величины ∑yi, ∑yi2 и ∑(pi1 - pi2) (обозначения описаны ниже) приведены в табл. П.6.1 для близнецовых пар и в табл. П.6.2 для контрольных пар.
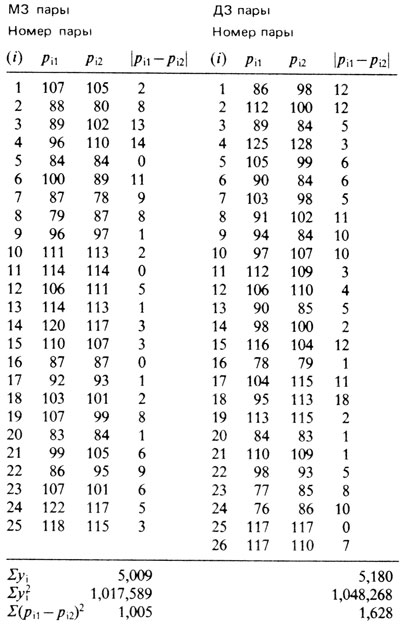
Таблица П.6.1. Показатель интеллектуального развития в близнецовых парах
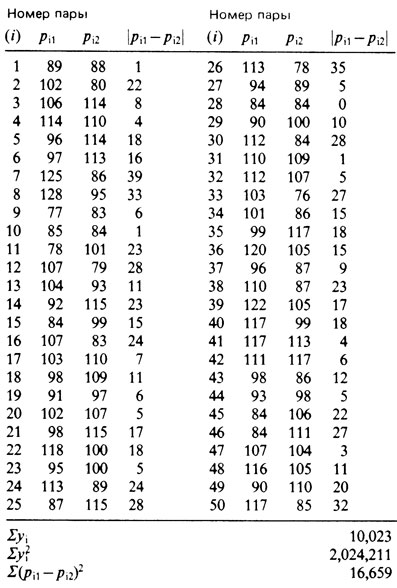
Таблица П.6.2. Показатель интеллектуального развития в контрольных парах
Из этих таблиц получаем
а) для МЗ пар в соответствии с уравнением
VˆPW = 1005/50 = 20,100, (П.6.6)
DQB = (1017589 - 50092/25)/48 = 291,370, (П.6.7)
VˆPB = (291,370 - 20,100)/2 = 135,635, (П.6.8)
rˆP,МЗ = 135,635 / 135,635+20,100 = 0,871.
Доверительный интервал (99%) для 1/2 ln 1+rP,МЗ/1-rP,МЗ = 1/2 ln 1+0,871/1-0,871 ± 2,58 1/√25-1,5 = 0,805 и 1,869, что соответствует доверительному интервалу
| e2×0,805 - 1 | = 0,667 | |
| e2×0,805 + 1 |
| e2×1,869 - 1 | = 0,954 | |
| e2×1,869 + 1 |
для rР,МЗ;
б) для ДЗ пар
VˆPW = 1682/52 = 31,308,
DQB = (1048268 - 51802/26)/50 = 325,052,
VˆPW = (325,052 - 31,308)/2 = 146,872,
| rP,ДЗ = | 146,872 | = 0,824. |
| e146,872 + 31,308 |
Доверительный интервал (99%) для 1/2 ln 1+rP,ДЗ/1-rP,ДЗ равен 1/2 ln 1+0,824/1-0,824 ± 2,58 1/√26-1,5 = 0,648 и 1,690, что соответствует доверительному интервалу от 0,570 до 0,934 для rР,ДЗ;
в) для контрольных пар
VˆPW = 16659/100 = 166,590,div>

DQB = (2024211 - 100232/50)/98 = 153,066,
VˆPB = (153,066 - 166,590)/2 = - 6,762,
| rP,CP = | - 6,762 | = - 0,042. |
| e166,590 - 6,762 |
Полученные выше доверительные интервалы для rP,МЗ и rР,ДЗ показывают, что коэффициент внутрипарной корреляции по IQ значимо отклоняется от 0 (Р < 0,01) для обоих типов близнецов. Это означает, что близнецы независимо от их зиготности более сходны по IQ, чем неродственные индивиды. Этот результат вполне закономерен, если IQ имеет генетическую основу, но все же не исключает возможность и чисто негенетического объяснения, поскольку близнецы имеют общую среду. Для исследования этой возможности мы тестируем гипотезу rP,МЗ = rР,ДЗ (нулевая гипотеза).
z = 1/2 ln 1+rP,МЗ/1-rP,МЗ - 1/2 ln 1+rР,ДЗ/1-rР,ДЗ = 0,168,
var z = 1/25-1,5 + 1/26-1,5 = 0,0834,
z/√var z = 0,582.
При нулевой гипотезе вероятность того, что значение z окажется больше найденного, превышает 10%. Это означает, что на основании сравнения коэффициентов внутрипарной корреляции в двух наших выборках близнецов нельзя отвергнуть гипотезу h2 = 0, т. е. гипотезу об отсутствии генетического вклада в изменчивость IQ в популяции. Следовательно, оценку h2 в соответствии с уравнением П.6.15
h32 = 2(rP,МЗ - rР,ДЗ) = 2 × (0,871 - 0,824) = 0,094
тоже нельзя считать значимо отличной от 0, что подтверждается рассмотрением стандартной ошибки оценки h2, которая приближенно равна 0,159 (в соответствии с уравнением П.6.16). Возможно, что разность внутрипарных корреляций МЗ и ДЗ близнецовых пар по IQ смещена, причем внутрипарная дисперсия IQ по неизвестной причине меньше у ДЗ близнецов, чем у МЗ. В этом случае следует использовать только две оценки h2, основывающиеся лишь на внутрипарных дисперсиях. Но даже если нет смещения, что очевидно для наших данных, все равно рекомендуется вычисление других оценок (уравнения П.6.12 и П.6.13). В нашем случае

(Компонента VM в знаменателе, представляющая собой дисперсию повторных измерений IQ, была опущена; здесь можно вставить надежность теста I-S-T.) Стандартные ошибки этих оценок можно вычислить по уравнению П.6.14
S. E. (h12) = 0,301, S. E. (h22) = 0,045,
что дает (почти) 95%-ный доверительный интервал от -0,23 до 0,95 для h12 и от 0,79 до 0,97 для h22. Эти два интервала частично перекрываются, но их пересечение отстоит от h32 более чем на две стандартные ошибки последней оценки. Таким образом, три оценки h2 оказываются несовместимыми. С другой стороны, h22 обычно завышает h2: предположение о том, что средовые внутрипарные различия совпадают для близнецов и неродственных контрольных пар, некорректно. Следовательно, различие между тремя полученными оценками можно объяснить этим смещением совместно с выборочными ошибками, которые велики из-за малого размера наших близнецовых выборок. В любом случае эти результаты трудно совместить с высокими значениями наследуемости, сообщаемыми для IQ некоторыми авторами [2086]. Приведенный нами пример иллюстрирует проблемы получения оценок наследуемости по близнецовым данным человека и заставляет проявлять осторожность в выводах, сделанных на основании этих оценок.
Для тех, кто интересуется использованием тонких генетических моделей для изучения количественных признаков у близнецов, рекомендуется работа Ивса [634]. Упомянем также, что для такого анализа необходимы выборки огромного размера.
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'