Приложение 7

Метод путевых коэффициентов

Основные понятия. Концепция наследуемости базируется на корреляциях между родственниками. Впервые корреляции стали вычислять биометрики. Позже Фишер показал, что определенные корреляции следуют и из законов Менделя. Наличие корреляций можно трактовать по-разному. Если А и В коррелируют, то А может быть частичной причиной В, В может быть частичной причиной А или А или В могут выступать в качестве общей причины С. Однако в генетике последовательность событий часто однозначна: корреляция между родителем и ребенком обусловлена тем фактом, что ребенок наследует свои гены от родителей и живет в среде, созданной ими же. Райт [961] предложил статистический метод, учитывающий это последовательное отношение.

"Качественную интерпретацию системы переменных ... удобно представить диаграммой, на которой стрелки используются для указания переменных, трактуемых как функции других переменных... . Неанализируемые корреляции можно представить двунаправленными стрелками для указания связи через общие факторы (рис. П.7.1).

Удобно измерять каждую переменную в терминах ее стандартного отклонения. Полагая

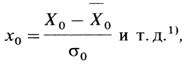
¹ (Х₀, Х₂, Х₃, ... обозначают переменные, Х‾₀, Х‾₂, Х‾₃, ... - их средние значения, тσ₀, σ₂, σ₃, ... - их стандартные отклонения и х₀, х₂, х₃, ... - соответствующие стандартизованные переменные.)

мы можем записать наилучшее линейное выражение для отклонений в терминах тех переменных, из которых стрелки выходят, и представить в виде

Коэффициенты p₀₂, p₀₃₃ и т. д. - абстрактные числа, которые я назвал путевыми коэффициентами, связаны с коэффициентами частной регрессии, точно так же, как коэффициент корреляции связан с общей регрессией. Они отличаются от коэффициентов корреляции, однако, тем, что имеют направление ... . Для любых двух переменных такой системы корреляция может быть представлена в виде суммы вкладов в одну из них. Пусть s обозначает факторы переменной х₀, а t - переменной x₁. Тогда

Дальнейший анализ компонентов корреляции приводит к легко запоминаемому принципу: любая корреляция может быть представлена в виде суммы вкладов всех путей на диаграмме (прямых или через общие факторы), которыми связаны две переменные, а каждый из этих вкладов представляет собой произведение коэффициентов, относящихся к элементарным путям. В каждом случае один из этих элементарных путей может быть неанализируемым двунаправленным путем, измеряемым коэффициентом корреляции".

Дальнейшее можно разъяснить на примере (рис. П.7.1). Справедливы следующие формулы (эти формулы получаются на основе теории частных корреляций и регрессий; элементарное объяснение см. в работе Ли [124]):

r₀₄ = p₀₂r₂₄ + p₀₃r₃₄ = p₄₇r₀₇ = p₀₂p₂₆r₆₇p₄₇ + p₀₃p₃₆r₆₇p₄₇ + p₀₃p_37p47.

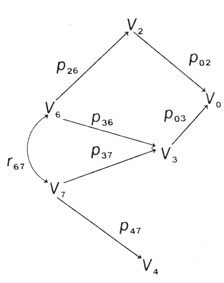
Рис. П.7.1

Здесь p_ij - путевой коэффициент от переменной V_j к переменной V_i, a r_ij - коэффициент корреляции между Vi и V_j (i, j = 0, 2, 3, 4, 6, 7).

Применение к данным по IQ человека. Чтобы объяснить суть подхода путевых коэффициентов, Райт использовал данные, собранные Бурксом (разд. 8.2.1.3), о корреляциях между родителями и приемными детьми, с одной стороны, и биологическими детьми - с другой. Две группы родителей были очень сходны. Помимо определения значений IQ для родителей и детей Бурке построил для каждой семьи "культуральный индекс", оценивающий, насколько благоприятна для развития интеллекта обстановка в семье. Затем для обеих групп родителей Бурке вычислил корреляции между IQ детей и культуральным индексом (r_СE) и между IQ детей и средних родителей (r_СР). Кроме того, была вычислена корреляция r_ЕР между IQ среднего родителя и средой. Теперь мы снова следуем анализу Райта, используя принцип путевых коэффициентов (рис. П.7.2).

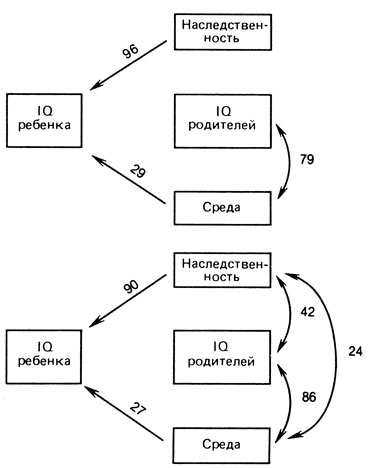
Рис. П.7.2

Приемные дети (в этих формулах r всегда обозначает коэффициент корреляции, а р - путевой коэффициент. Индексы имеют следующий смысл: P - IQ среднего родителя, C - IQ ребенка, E - культуральный индекс)

Это так называемая теорема полной причинной детерминации. Она следует из того факта, что корреляция переменной с самой собой равна 1.

Собственные дети

"Если IQ воспитывающих родителей связан с IQ детей только через корреляцию с домашней средой, то корреляция родитель-ребенок должна быть произведением двух промежуточных коэффициентов. Соответствующий подсчет дает значение корреляции между средним родителем и средой (+ 0,79), очень близкое к наблюдаемому в контроле (+ 0,86). Это указывает на отсутствие иного влияния родителей, кроме как через общую среду, измеренную реально (в биологических семьях). Только 9% детерминации дисперсии обусловлены домашней средой (= 0,292), что дает в качестве остатка 91% детерминации и путевой коэффициент 0,96. В какой степени это относится лишь к наследственности, а в какой - к неизмеряемым средовым факторам, судить нельзя, но, поскольку домашняя среда, вероятно, наиболее важный средовый фактор ..., можно предположить, что остаточная часть высоко наследуема.

В других группах ситуация сложнее. Мы можем сразу выписать три уравнения, представляющие разложение трех известных корреляций (r_ЕР, r_СЕ и r_СР). Если предположить, что единственным фактором, влияющим на IQ детей, помимо среды является наследственность, то мы сможем выписать четвертое уравнение, выражающее полную детерминацию. Но в этом случае надо определить пять коэффициентов. По данным контрольной группы это сделать невозможно. Однако у нас есть другой источник информации. Контрольная группа родителей была тщательно отобрана для сравнения с воспитывающей группой. Предположительно домашняя среда обладает очень похожими эффектами в этих двух случаях. Мы должны суметь извлечь средовые коэффициенты из данных о воспитывающих родителях".

Путевой коэффициент р_СЕ нельзя перенести прямо, потому что в контрольных данных на него влияет корреляция между наследственностью и средой. Однако "можно заключить, что отношение р_СЕ:р_СН должно быть одинаковым в этих двух случаях, что дает пятое уравнение". Эти уравнения были решены, результаты приведены на рис. П.7.2.

В общем случае количество уравнений должно быть по крайней мере равно числу путей или коэффициентов корреляции, которые нужно определить. Можно математически показать, что путевые коэффициенты эквивалентны стандартизованным коэффициентам регрессии, т. е. коэффициентам регрессии, которые относятся к стандартизованным переменным, а не к переменным в исходных физических единицах. Дело исследователя, проводить ли анализ, используя методы стандартной частной регрессии или частной корреляции, или же воспользоваться путевыми коэффициентами. Преимущество последнего метода состоит в том, что диаграмма дает прямой и убедительный способ визуализации компонент, которые влияют на признак.

Последующее развитие метода. В последние годы Мортон [803] усовершенствовал этот подход, введя ряд дополнительных корреляций. На рис. П.7.3 показана путевая диаграмма для корреляции между сибсами. Здесь предполагается, что фенотипы двух детей X и Y являются "результатом действия четырех аддитивных факторов: общей среды (С), случайной среды (Е), генотипа среднего родителя (G) и сегрегации генотипа среднего родителя (S). Генотип среднего родителя и общая среда коррелируют (r), а общая среда (почти) линейно измеряется индексом (I), основанным на таких переменных, как общественно-экономическое положение, доход, образование родителей, соседство, школьный район, культурный уровень родителей, психологическая обстановка в семье".

Рис. П.7.3. Путевая диаграмма для корреляции между сибсами [803]

Используя метод путевых коэффициентов, Мортон и коллеги пытались ответить на вопрос, являются ли различия в средних уровнях IQ у черных и белых американцев следствием генетических причин или они - результат действия социальных факторов. Авторы пришли к выводу, что основную роль в снижении IQ играют именно социальные факторы (V Международный конгресс по генетике человека, 1976).

Вероятно, такой вывод, в известной степени справедлив, но методологическая основа, на которой он базируется, была подвергнута суровой критике (Голдбергер [683], Тейлор [2214]). Серьезным недостатком метода путевых коэффициентов, по их мнению, является то, что он не обеспечивает количество уравнений, достаточное для оценки необходимых параметров, поэтому некоторые из них по предположению должны быть равны 0. Весьма сомнительным представляется и оперирование предполагаемыми факторами. Общественно-экономическое положение и образование, например, которые учитываются при оценке влияния "общей среды", могут иметь генотипические компоненты. Мы также не уверены в том, что этот метод биометрического анализа внесет существенный вклад в наше понимание влияния генетических факторов.

Сам Райт "никогда не выступал с нелепой претензией, что теория путевых коэффициентов дает общую формулу для вывода причинных отношений". Наоборот, априорное знание причинных отношений является предварительным требованием для применения этого метода, и результаты, полученные с его использованием, зависят от корректности предполагаемых причинных отношений.