
§ 3. Вычисление основных параметров (показателей) вариационного ряда
Для характеристики вариационного ряда требуется вычисление некоторых важных параметров. В первую очередь это среднее арифметическое, которое отражает многие свойства всей совокупности - выборки. Даже изучение "типичной" по данному признаку особи (клетки, наблюдения) дают меньше сведений о свойствах данной совокупности, чем среднее арифметическое. Эта величина именованная и может быть выражена дробным числом. Казалось бы, что число щенков, например, не может быть нецелым. Но, так как изучается изменчивость совокупности и ее характеристика, естественно, что среднее арифметическое отличимо от характеристики каждой отдельной особи (может быть именно на дробное число).
Для вычисления среднего арифметического (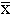 ), если есть под рукой суммирующая машина, следует сложить все значения вариант выборки и разделить на число наблюдений (опытов).
), если есть под рукой суммирующая машина, следует сложить все значения вариант выборки и разделить на число наблюдений (опытов).
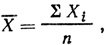
где ∑ - знак суммы, X1 - отдельная варианта выборки, а n - число наблюдений.
Если суммирующей машины нет, то среднее арифметическое определяют по формуле:
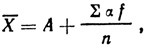
где А - условное среднее, т. е. та величина, которая входит в состав модального класса (класса с наибольшим числом вариант), ∑αf - сумма произведений отклонений от условного среднего (α) на частоту (f) (см. табл. 6). Отсчет α ведут от условного среднего в сторону классов с меньшим числом вариант (-) и в сторону классов с большим числом вариант (+) (графа 3). Графа 4 получается от переумножения α на f.
Не менее важным показателем вариационного ряда, мерой изменчивости изучаемого признака (выражением степени разброса данных, а следовательно, и крутизны, степени наклона ветвей линейного полигона распределения - см. рис. 36) является среднее квадратическое отклонение - σ (сигма). Она вычисляется по формуле:
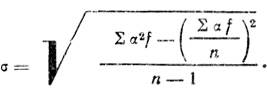
Для вычисления среднего квадратического отклонения в таблицу вводят еще графу 5. Эта графа состоит из произведений отклонений (α), возведенных в квадрат*, на частоты (f).
* (Произведение всегда положительно, так как минус на минус дает плюс.)
Среднее квадратическое отклонение, как и среднее арифметическое, является величиной именованной.
Таким образом, чтобы вычислить среднее арифметическое (без суммирующих машин), а также среднее квадратическое отклонение, необходимо составить таблицу.

Таблица 6. Последовательность операций при вычислении среднего арифметического и среднего квадратического отклонения (для ряда распределения 70 самок серебристо-черных лисиц по числу щенков в одном помете)
Примером такой таблицы может служить табл. 6 - последовательность операций при вычислении 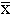 и ο (на примере ряда распределения 70 самок серебристо-черных лисиц по числу щенков в одном помете).
и ο (на примере ряда распределения 70 самок серебристо-черных лисиц по числу щенков в одном помете).
Подставляя значения, полученные в результате суммирования цифр графы 4 в формулу III, узнаем среднее арифметическое для выборки I (число щенков):
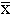 = 4 + 30/70 = 4,43 щенка на один помет самки*.
= 4 + 30/70 = 4,43 щенка на один помет самки*.* (Расчеты производят обычно с точностью на один порядок больше, чем точность измерения, т. е., если хотят получить результат с точностью до 0,1, параметрические расчеты надо делать с точностью до 0,01.)
Среднее квадратическое отклонение для данного случая определяется по формуле IV:
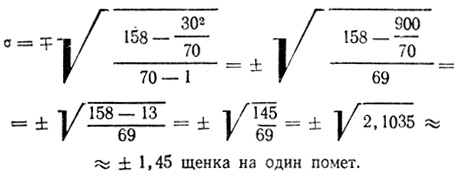
Чем больше величина среднего квадратического отклонения при близких по величинам средних арифметических, тем выше степень изменчивости данного признака. Если средние арифметические разных выборок будут отличаться друг от друга, то судить об изменчивости по величине о невозможно. Вследствие этого для характеристики и сравнения изменчивости разных признаков вводят коэффициент вариации (СV), показывающий, какую долю среднее квадратическое отклонение составляет от среднего арифметического. Коэффициент вариации вычисляют по формуле:
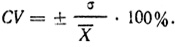
В данном примере CV = ± 1,45/4,49*100% = ± 0,327*100% = ±33%.
Кроме перечисленных выше статистических величин, необходимо (особенно при сравнении двух или более опытов, наблюдений) вычислить ошибку среднего арифметического, которая неизбежно происходит - при наблюдениям (ибо мы берем какую-то относительно небольшую выборку из генеральной совокупности). Ошибку среднего арифметического вычисляют по формуле:
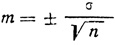
В нашем случае
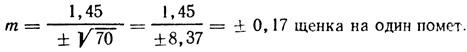
Если необходимо сравнить два аналогичных наблюдения и узнать, различны ли две выборки (не описывая каждую из них в отдельности), то применяют коэффициент достоверности различия средних арифметических Т (от англ. Test - испытание), метод, который вычисляют по формуле:
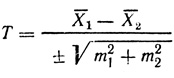
(в числителе из большего среднего арифметического вычитают меньшее).
Если при этом полученное значение равно или больше 2,31, то с вероятностью 0,01 (1%) эти выборки различны, а значение Т достигает 3,01 или выше - сравниваемые выборки различаются с достоверностью 0,001 (т. е. 0,1%). Более точные цифры Т, соответствующие той или иной степени разностей, находят по специальным таблицам в руководствах по статистике.
Представим себе, что, кроме разобранного выше примера с параметрами 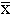 = 4,43 и m = 0,17 щенка, имеется еще одна выборка с параметрами
= 4,43 и m = 0,17 щенка, имеется еще одна выборка с параметрами 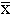 = 4,73, и m = 0,19 щенка. Обозначим большее среднее арифметическое (4,73) как
= 4,73, и m = 0,19 щенка. Обозначим большее среднее арифметическое (4,73) как 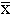 , его ошибку m1 (0,19), а меньшее среднее арифметическое (4,43) как
, его ошибку m1 (0,19), а меньшее среднее арифметическое (4,43) как 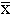 2, его ошибку (0,17) как m2 и подставим их значения в формулу VII:
2, его ошибку (0,17) как m2 и подставим их значения в формулу VII:
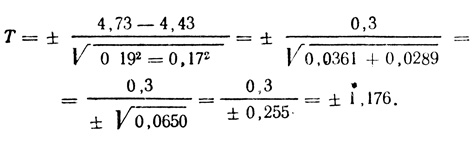
Коэффициент достоверности различий средних арифметических в этом случае много ниже даже первого порога различий (1,96), что позволяет обоснованно утверждать о принадлежности сравниваемых совокупностей к одной генеральной совокупности.
Вычисление основных параметров вариационного ряда, сравнение их с другими выборками имеют большое практическое значение при анализе экспериментов или наблюдений.
Теперь нам осталось вычислить основные показатели для выборки 2 (массу 70 самок серебристо-черных лисиц). Прежде всего составим табл. 7 - последовательность операций при вычислении среднего арифметического и среднего квадратического отклонения (обозначение граф см. в табл. 6).

Таблица 7. Последовательность операций при вычислении среднего арифметического и среднего квадратического отклонения для ряда (масса в килограммах) 70 самок серебристо-черных лисиц
При вычислении среднего арифметического и среднего квадратического отклонения в формулы вводят классовый промежуток, обозначаемый греческой буквой к (лямбда).
Формула определения среднего арифметического выглядит так:
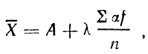
где А, находящаяся в классе 4,5-4,9, равна половине этого расстояния - 4,65, а λ = 0,5 кг.
Подставляем значение в формуле определения средней массы самки:
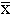 = 4,65 + 0,5*34/70 = 4,65 + 0,5*0,48 = 4,65+0,24 = 4,89 кг
= 4,65 + 0,5*34/70 = 4,65 + 0,5*0,48 = 4,65+0,24 = 4,89 кгСреднее квадратическое отклонение определяют по формуле:
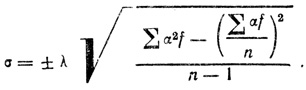
Подставив значение составных частей формулы, получим:
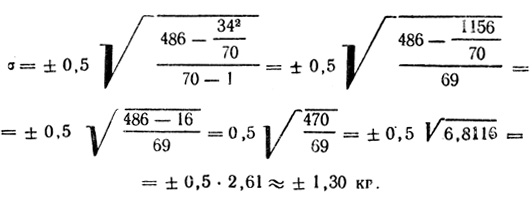
Все остальные параметры вычисляют по формулам, приведенным выше.
Коэффициент вариации находят по формуле V:
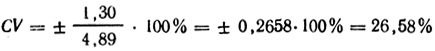
Ошибку среднего арифметического вычисляют по формуле VI:
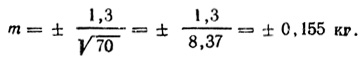
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'