§ III.2. Флуктуации вокруг равновесных состояний

Чтобы охарактеризовать различие между флуктуациями вблизи стационарного состояния и вблизи устойчивого равновесия, начнем это обсуждение с рассмотрения классического примера флуктуаций вблизи состояния равновесия - с эренфестовской модели урн (см. также рис. 3).

Имеются две урны и некоторое (большое) число - скажем, 2N - шаров, произвольно распределенных между этими урнами. Шары пронумерованы от 1 до 2N.

Игра состоит в том, что случайно выбирается номер (можно, например, тянуть жребий, бросать кость или использовать любую другую лотерейную процедуру), после чего шар с соответствующим номером переносится из одной урны в другую. Если эту процедуру повторить достаточно много раз, то результатом будет - независимо от начального распределения - равномерное распределение 2N шаров по двум урнам.

Эту модель придумали П. и Т. Эренфесты [62], а впоследствии ее стохастические аспекты рассматривали Д. тер Хаар и К. Грин [63], М. Кац [64], М. Клейн [65] и другие. К. Кольрауш и Э. Шредингер [66] проверили эту модель экспериментально. Стохастическое рассмотрение модели (например, у М. Каца) выявляет следующие ее особенности:

1. Равновесное состояние, хотя оно и подвержено флуктуациям, обладает устойчивостью. В среднем каждая урна будет содержать N шаров.

2. Вблизи равновесного состояния будут происходить флуктуации: одна урна будет содержать N + n, другая - N-n шаров, причем n может принимать любое значение от -N до +N. По аналогии с теоремой Больцмана мы можем охарактеризовать рассматриваемую модель функцией распределения

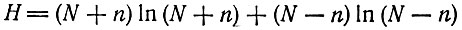(III.1)

или для n << N

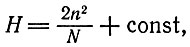(III.2)

откуда видно, что флуктуации распределены симметрично по отношению к n = 0.

3. Вероятность найти (N + n) шаров в одной и (N - n) шаров в другой урне равна

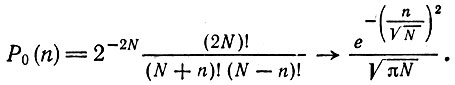(III.3)

Это распределение вероятностей стационарно по отношению к стохастическим уравнениям, т. е. оно не зависит от времени, тогда как n постоянно флуктуирует. Распределение вероятностей симметрично по отношению к n = 0 (распределение Гаусса), причем его полуширина пропорциональна 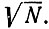Большие флуктуации, порядка n = N, крайне маловероятны. В самом деле,

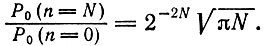(III.4)

4. Ту же величину имеет и τ(n = 0)/τ(n = ±N) - отношение "времен возврата" (т. е. средних интервалов времени, через которые повторяются данные макросостояния). Время возврата минимально при n = 0.

Из всего этого следуют важные выводы. Равновесие является "устойчивым" состоянием. Флуктуации обладают свойством саморегуляции; чем больше отклонение в одном направлении, тем больше вероятность его обращения, т. е. восстановления равновесия. Средние флуктуации пропорциональны √N, поэтому они несущественны при больших N. Отношение времен возврата [см. уравнение (III.4)] показывает, насколько редко происходят на самом деле большие флуктуации, если N - большое число. Эта модель имела историческое значение для понимания природы необратимого процесса по сравнению с флуктуацией [67].