§ III.3. Флуктуации в стационарном состоянии

В предыдущем примере две урны представляли собой два эквивалентных состояния, между которыми в системе 2N эквивалентных шаров устанавливалось устойчивое равновесие. Давайте изменим нашу модель: вместо двух урн возьмем только одну, но теперь при вытягивании жребия предусмотрим не один, а два билетика для каждого шара: белый и черный. Каждый раз, когда мы вытащим белый билетик, мы будем добавлять еще один шар в урну, а вытащив черный билетик, будем удалять один шар из урны. В сущности, если считать шары эквивалентными, нам больше не нужна их нумерация. Впрочем, если нас интересует эволюция отдельных видов, можно сохранить нумерованные шары; при этом определенные номера будут дублироваться всякий раз, когда вытаскивается соответствующий белый билетик. Мы должны обеспечить также, чтобы каждому шару в урне всегда соответствовали ровно два билетика (белый и черный); поэтому удаление или добавление шара всегда должно сопровождаться удалением или добавлением двух соответствующих билетиков.

Эта модель представляет собой типичную задачу о стационарном состоянии, где вероятности образования и распада равны и пропорциональны имеющемуся числу частиц. Детерминистическое уравнение снова дало бы распределение, не зависящее от времени. Однако это распределение метастабильно вследствие того факта, что флуктуации скоростей добавления и удаления не зависят друг от друга, и поэтому здесь нет саморегуляции. Этот пример тесно связан с задачей химической кинетики, которую мы обсудим ниже: для этого сформулируем ее в более реалистических терминах.

Вспомним "информационный ящик", введенный в § II.1. Этот ящик имеет полупроницаемые стенки, через которые могут проходить мономерные единицы в низко- или высокоэнергетическом состояниях, тогда как все макромолекулярные носители информации и весь аппарат репликации (ферменты и т. д.) остаются внутри ящика. Условия внутри ящика благоприятствуют синтезу макромолекул; однако здесь возможен только матричный синтез, т. е. репликация. Сформулируем три задачи, которые иллюстрируют стохастические аспекты отбора и будут количественно рассмотрены в следующем параграфе:

1. Дано большое число N различных последовательностей (для простоты - равной длины), причем каждая последовательность имеется лишь в одном экземпляре; образование новых последовательностей может происходить только путем матричного синтеза, причем редупликация является точной, т. е. ошибки отсутствуют (Q_k = 1). Все кинетические факторы образования и распада F_k и R_k равны, т. е.

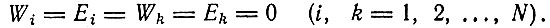
(Равенство W_i = E_i имеет место, поскольку Q_i = 1.) Согласно детерминистической теории, такая система находилась бы в стационарном состоянии, и в ней ничего не происходило бы. Это, очевидно, не может быть верным для каждой отдельной копии. Это может быть приблизительно верным для всего множества копий, по крайней мере на протяжении некоторого интервала времени, если только мы не различаем отдельные копии (все они вырождены по отношению к кинетическим свойствам). Наш вопрос заключается в том, какова истинная судьба суммарного содержимого ящика, а также отдельных классов носителей информации. (Необходимо подчеркнуть, что мы начинаем с N различных копий, причем все они могут представлять собой различные "сообщения".)

2. Условия те же, что и в первой задаче, но на этот раз допускается возможность ошибок при воспроизведении, т. е. Q_k < 1. Однако для всех копий будем, как и прежде, требовать, чтобы W_i = W_k (i, k = 1, 2, ..., N), Теперь из-за ошибок в процессе репликации могут возникать новые виды последовательностей. Нас снова интересует, как меняется во времени суммарное и индивидуальное информационное содержание.

3. Начиная с условий задачи 2, допустим, наконец, что кинетические параметры образования и распада, т. е. W_i, W_k (i, k = 1, 2, ..., N), могут быть различны. Без регулирования потоков эта система может находиться в стационарном состоянии только вначале, когда средняя общая скорость образования равна средней общей скорости распада. Однако стационарное состояние можно поддерживать, если регулировать приток мономерных единиц и (или) растворителя в соответствии с теми ограничениями, которые были определены в гл. II. Здесь нас интересует эволюционное поведение индивидуальных видов, особенно если они возникают как одиночные мутантные копии, имеющие селективное преимущество W_i > E¯.

Прежде чем начать математическое рассмотрение, попытаемся представить себе, какого поведения системы можно ожидать. В первой задаче система, очевидно, "замкнута" по отношению к добавлению любой новой информации (которая может быть введена только посредством ошибок воспроизведения). Вместе с тем всякий раз, когда отдельный неизбыточный носитель информации разлагается, не успев редуплицироваться, происходит потеря информации. Это будет случаться постоянно, поэтому количество индивидуальной неизбыточной информации будет все время уменьшаться. Если суммарное число носителей информации очень велико, такие "отрицательные" флуктуации могут компенсироваться "положительными" флуктуациями (т. е. размножением других копий). Таким образом, информационное содержание будет сначала сужаться до нескольких (или даже до одной) весьма избыточных последовательностей, после чего вся популяция в конце концов вымрет. Такая судьба популяции в целом неизбежна, потому что флуктуации образования и распада происходят независимо друг от друга. Как показывает рис. 6 (обсуждение см. в подписи), полное вымирание может произойти даже за относительно короткое (по сравнению с соответствующими временами возврата для равновесных флуктуаций; см. § III.2) время.

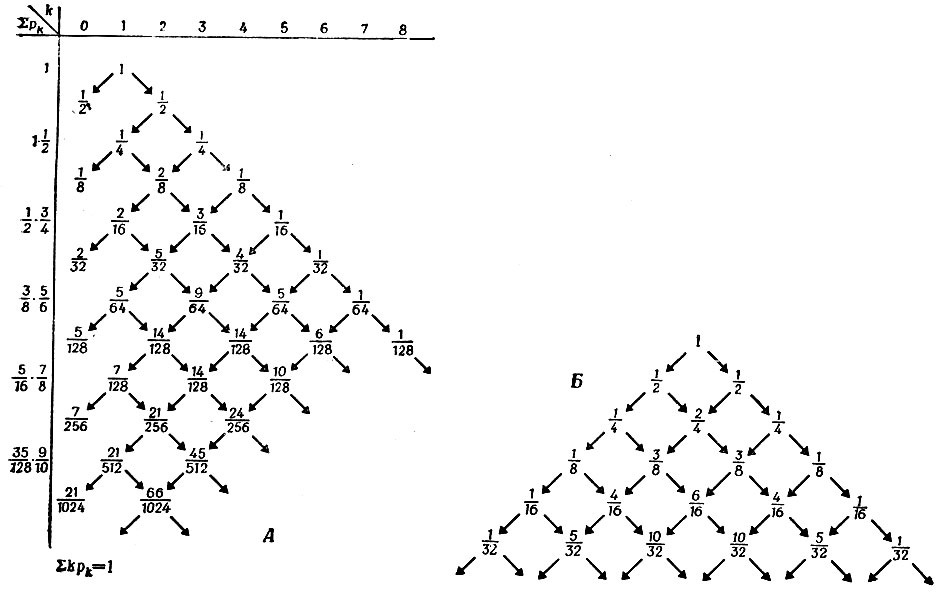
Рис. 6. Графическое представление вероятностей для модели стационарного состояния. Числа k по горизонтали означают избыточность каждой копии. Отметим, что здесь представлены лишь вероятности, а не эволюция во времени. Каждый шаг означает изменение численности популяции на единицу; вероятности добавления и удаления одинаковы. Временные интервалы между переходами уменьшаются с ростом k - они обратно пропорциональны k. Такая форма представления данных выбрана для того, чтобы продемонстрировать асимметрию случайного блуждания, которая обусловлена 'вымиранием' при k = 0. Если бы этой асимметрии не было, т. е. если бы каждое последующее состояние получалось из предыдущего с вероятностью ¹/₂ (допуская также отрицательные значения k), то получился бы 'треугольник Паскаля', в котором члены каждого горизонтального ряда представляют собой биномиальные коэффициенты, деленные на сумму всех коэффициентов, отвечающих этому ряду. Можно видеть, что вымирание изменяет вероятности несимметричным образом, так что в обоих треугольниках совпадают только правые границы. Допустим, что мы хотим предсказать вероятность вымирания. Начнем с любого числа k и рассмотрим случайное блуждание соответствующем треугольнике с вершиной в начальной точке. Так как вероятности перехода для каждого направления равны, то потребуется в среднем k² шагов, чтобы достичь состояния вымирания (т. е. k = 0). Так как временные интервалы убывают обратно пропорционально k, можно предсказать, что для вымирания потребуется в среднем время, заключенное между k-кратным и k²-кратным элементарного времени 1/F_i. Искомое время должно быть ближе к но больше его. При t = k²/F_i вымирание должно наступить почти наверное. Кратчайшее время, за которое в этой модели можно достичь нулевого состояния (начиная с k), дается выражением

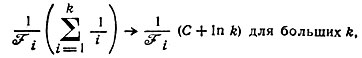
где С - постоянная Эйлера:

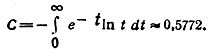
Поскольку мы не различаем отдельных носителей информации, мы можем ожидать, что точно такая же судьба постигнет всю популяцию во втором примере. Кинетические параметры для всех видов одинаковы и суммарное образование точно компенсируется суммарным распадом. Однако для отдельного носителя информации (т. е. индивидуального информационного содержания) эволюционное поведение значительно отличается от поведения в первом случае. Если факторы усиления A_k точно равны факторам разложения D_k, но факторы качества Q_k меньше единицы, каждый вид должен вымереть, потому что для каждого вида W_k = A_kQ_k - D_k < 0. В качестве компенсации эта система постоянно производит новую информацию посредством ошибок в процессе копирования. Она "беспорядочно дрейфует в информационном пространстве" до тех пор, пока, как и в первом случае, вся популяция не будет стерта "флуктуационной катастрофой".

Только в третьем случае мы можем ждать устойчивого и воспроизводимого поведения. Здесь система будет отбирать вид с максимальным W_k (допуская, что вообще имеется вид, для которого W_k > 0). До тех пор пока этот вид существует только в небольшом числе копий, он будет подвергаться опасности вымирания из-за флуктуаций. Однако, чем больше растет его численность, тем устойчивее он будет становиться и в конце концов станет доминировать в популяции в соответствии с детерминистическими уравнениями. Возникает интересный вопрос: имеется ли "точка, откуда нет возврата" в случайном блуждании, изображенном на рис. 6, если вероятности благоприятствуют росту? Каждому летчику знакома такая точка на взлетной полосе; когда он ее прошел, он должен взлететь. По аналогии мы можем искать такую "критическую" точку на оси концентраций, которая - если она пройдена мутантом - не оставляет возможности для "возврата".

Количественные ответы на все эти вопросы можно получить только из количественного теоретического рассмотрения.