
§ III.4. Стохастические модели как цепи Маркова
Стохастическое исследование различных эволюционных моделей в настоящее время продолжается. Сейчас мы можем дать принципиальные ответы на большинство сформулированных выше вопросов, используя результаты, полученные ранее для некоторых простых линейных моделей.
А. Бартоломей [68] недавно изложил стохастическую теорию стационарных линейных процессов "рождения и гибели". Аналогичные проблемы рассматривали другие авторы: например, случай простой автокаталитической (прямой) реакции рассмотрен М. Дельбрюком еще в 1940 г. [69]. Существует обзор литературы по применениям теории случайных процессов к задачам химической кинетики (см. Д. Мак-Кварри [70]).
Следующее обсуждение будет основано на элегантном изложении Бартоломея [68], в котором он использовал метод Q-матрицы Дуба [71]. Элементы метода Дуба и процедура Бартоломея суммированы в табл. 9 и 10.
Таблица 9. Метод Q-матрицы Дуба для случайных процессов, по А. Бартоломею [68]
I. Требования
"Функция переходных вероятностей" pij(t) для перехода из состояния 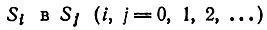 определяется как условная вероятность
определяется как условная вероятность
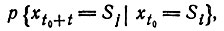 (1)
(1)т. е. вероятность того, что случайная переменная xi будет иметь значение Sj в момент времени t0 + t, если она имела значение Si в момент времени t0. Процесс (xt, 0 ≤ t < ∞) называется стационарной цепью Маркова, если вероятности перехода удовлетворяют следующим условиям:
 (2)
(2) (3)
(3)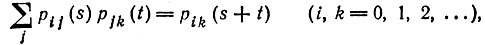 (4)
(4)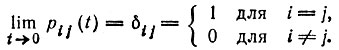 (5)
(5)II. Определение матрицы Q = (qij)
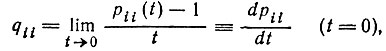 (6)
(6)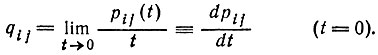 (7)
(7)Требования I и определения II используются для построения следующей системы дифференциальных уравнений (p· = dp/dt):
III. а) Прямая система
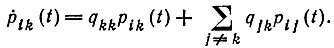 (8)
(8)б) Обратная система
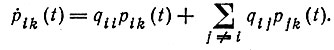 (9)
(9)Прямая система описывает, что происходит в последнем временном интервале (t → 0) до перехода; обратная система описывает, что происходит в первом временном интервале после перехода. Это отражено в суммах: в случае прямой системы варьируют конечное состояние, в случае обратной системы варьируют начальное состояние.
IV. Общее решение
Для конечного числа состояний и при данных начальных условиях, например при условии (5), единственное решение для обеих систем может быть дано в матричной форме, как показано Дубом [71]:
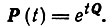 (10)
(10)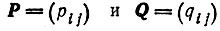
- матрицы, 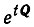 получается последовательным суммированием членов разложения экспоненты в ряд
получается последовательным суммированием членов разложения экспоненты в ряд
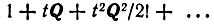 (11)
(11)Для определения величин pij(t) и соответствующих qij некоторым свойствам детерминистических уравнений дается вероятностная интерпретация (ср. табл. 10).
Таблица 10. Линейные процессы рождения и гибели как цепи Маркова, по А. Бартоломею [68]
Дано детерминистическое уравнение
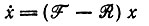 (1)
(1)и его решение
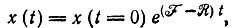 (2)
(2))
где F и R - константы.
Для малого интервала времени между t1 и t1 + Δt1 результирующее изменение Δx1 в популяции равно
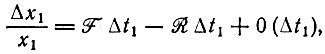 (3)
(3)где 0(Δt1) включает в себя все бесконечно малые высших порядков. Δt1 выбирается достаточно малым, чтобы в этом временном интервале имели конечное значение лишь вероятности образования или распада одной копии, которые даются выражениями
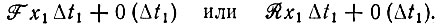 (4)
(4)Тогда численность популяции может измениться только на плюс или минус единицу; таким образом, разрешены только переходы Si → Si-1 или Si → Si+1 (i = 1, 2, ...), и эти переходы могут происходить только в результате одного элементарного события (множественные рождения и гибели, дающие в сумме изменение на ±1, исключаются). Далее, переход S0 → S1 имеет нулевую вероятность, так как, достигнув состояния S0, система "вымирает". Используя разложение pij(t) в ряд
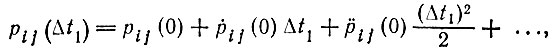
строим Q-матрицу согласно уравнениям (6) и (7) в табл. 9 и после сравнения с выражениями (4) в настоящей таблице получим
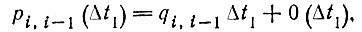 (5)
(5)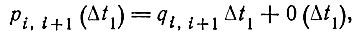 (6)
(6)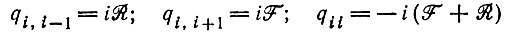 (7)
(7)(i = 0, 1, 2, ... - состояния популяции).
Теперь можно построить "прямые" и "обратные" уравнения, приведенные в табл. 9:
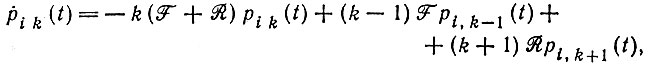 (8)
(8)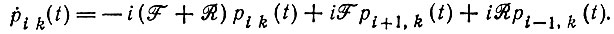 (9)
(9)Чтобы решить эти уравнения, введем "производящую функцию вероятностей":
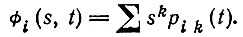 (10)
(10)Из ∂ф/∂s и ∂ф/∂t получим
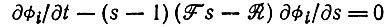 (11)
(11)с дополнительным уравнением
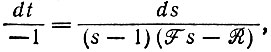 (12)
(12)
интегрирование которого для двух случаев 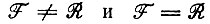 ведет к общему решению уравнения в частных производных для производящей функции:
ведет к общему решению уравнения в частных производных для производящей функции:
1. F ≠ R
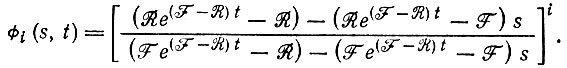 (13)
(13)Разложение по степеням s дает значения коэффициентов при sk, которые, по формуле (10), равны соответствующим вероятностям:
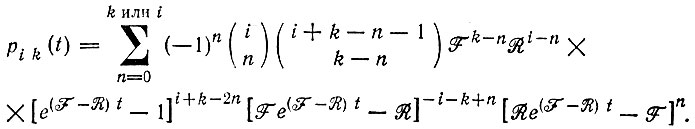 (14)
(14)Верхний предел суммирования равен k, если 0 < k < i, и равен i, если k ≥ i. имеем
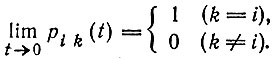 (15)
(15)Математическое ожидание i равно
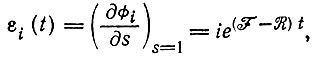 (16)
(16)т. е. совпадает с результатом детерминистической теории; дисперсия i равна
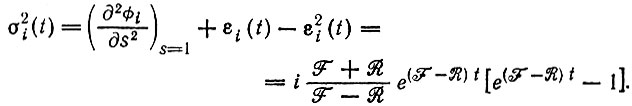 (17)
(17)2. F = R. Решение аналогично:
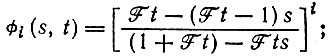 (18)
(18)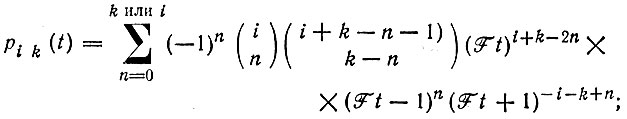 (19)
(19)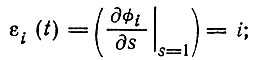 (20)
(20)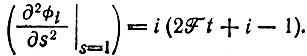 (21)
(21)Рассматриваемый процесс, детерминистический аспект которого выражен уравнением (II.10) с φi l = 0, Fi и Ri = const, представляет собой стационарную цепь Маркова
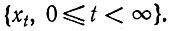 (III.5)
(III.5)Время (t) является непрерывным параметром; xi - случайная популяционная переменная - принадлежит дискретному счетному множеству состояний S0, S1 .... Переход из одного состояния (Si) в другое (Sj) описывается вероятностью перехода Pij(t). Это вероятность того, что система, находящаяся в состоянии Si при t = 0, достигает состояния Sj в момент времени t. Знание pij(t) позволяет определить математическое ожидание и дисперсию для населенности любого состояния во время t, если заданы начальные условия для t = 0. Вероятности перехода для линейного процесса рождения и гибели, вычисленные в табл. 10, дают основу для дальнейшего обсуждения.
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'