§ III.5. Количественное рассмотрение трех прототипов отбора

Случай 1. Вернемся назад к первой из трех задач о стационарном состоянии (см. § III.3) и спросим, какова вероятность выживания или вымирания системы, которая определяется параметрами 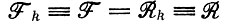(для всех видов k, имеющихся в наличии). Если при t = 0 вся популяция состояла из N видов, вероятность вымирания (для F = R) следует из выражения (19), приведенного в табл. 10:

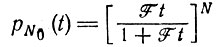(III.6)

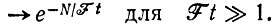(III.7)

Эта вероятность близка к единице для Ft >> N. Уже при Ft = N мы имеем

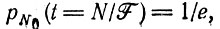(III.8)

т. е. вероятность вымирания популяции больше ¹/₃. При Ft = N² имеем

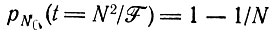(III.9)

- вымирание почти достоверно.

Математическое ожидание величины популяции остается равным N независимо от t [см. выражение (20) в табл. 10]. Однако дисперсия растет со временем. При t = N/F она становится равной

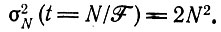(III.10)

Итак, мы нашли, как и предполагали ранее (см. подпись к рис. 6), что стационарная популяция, состоящая при t = 0 из N видов, имеет среднюю продолжительность жизни, заключенную между N/F и N²/F. При t = N²/F вымирание почти достоверно.

Посмотрим теперь, какова судьба N различных видов, если вначале каждый из них имелся только в одном экземпляре.

Согласно выражению (19) в табл. 10, вероятность того, что единственная копия размножится в количестве k экземпляров, равна

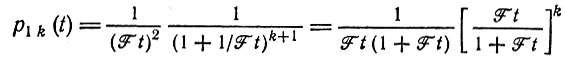(III.11)

(для k ≥ 1), и вероятность того, что этот вид вымрет, равна

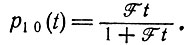(III.12)

Просуммировав уравнения (III.11) по всем k ≥ 1 и добавив к сумме уравнение (III.12), получим

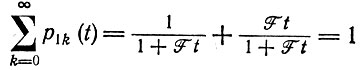(III.13)

в согласии с уравнением (3) в табл. 9.

Для любого k ≥ 1, p_1k(t) как функция t проходит через максимум при

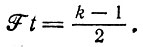(III.14)

При этом р_1k достигает значения

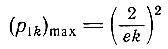(III.15)

(е - основание натуральных логарифмов). Если нас интересует, например, в какое время и для какого k максимальное p_1k будет равно 1/N, мы получим

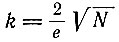(III.16)

или

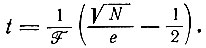(III.17)

Будем рассматривать p_1k(t) как функцию k. Для Ft >> 1 получается асимптотическое выражение

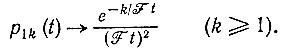(III.18)

Это распределение, т. е. p_1k(t) как функция k (в логарифмической шкале) при данном t₁, показано для t₁ = N/F на рис. 7. Как можно видеть, вероятности почти не зависят от k - p_1k(N/F) = 1/N², пока k не достигнет N по порядку величины, после чего начинается экспоненциальный спад. В то же время вероятность вымирания равна

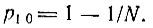(III.19)

Учитывая, что

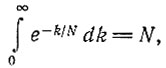(III.20)

распределение вероятностей можно аппроксимировать константой 1/N² в интервале от k = 1 до N, причем при k = 0 происходит скачок до значения 1 - 1/N. Итак, начиная с одной копии при t = 0 имеются примерно равные шансы для любой степени усиления k от 1 до N. Так как вначале (t = 0) мы имели N различных отдельных копий, вероятность, что одна из них усилится до численности >N/2, уже равна 50% (т. е. 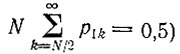при t = N/F. В то же время большинство других копий вымирает, так как

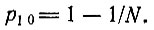
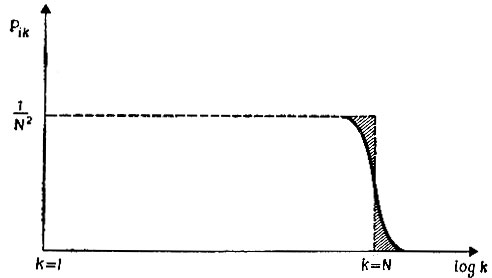
Рис. 7. Распределение вероятностей для 'выживших' при t₁ = N/F, согласно (III.18)

Математическое ожидание 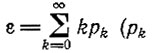находятся по формуле III.11) для каждого вида снова остается равным единице и не зависит от времени, тогда как дисперсия для каждого вида растет; например, для Ft = N она равна

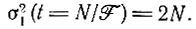(III.21)

В заключение отметим:

Разнообразие носителей информации сужается до нескольких, или даже до одного, весьма избыточного вида, после чего все носители информации вымирают. Такое селекционное поведение, вызванное автокаталитической природой процесса образования, представляет собой типичный случай "выживания выживших". В группе, где все индивидуумы имеют равные шансы на выживание, нет другого критерия отбора, кроме его исхода, т. е. самого факта выживания.

Этот тип чисто "стохастического" выживания в стационарном состоянии нереален, потому что фактор качества никогда не может быть точно равным единице. Его следует отличать от отбора дарвиновского типа, для которого можно сформулировать оптимизационные критерии выживания.

Случай 2. Во второй задаче, предложенной в § III.3, необходимо качественно различать решения, относящиеся ко всей популяции и к отдельным индивидуумам. Для всей популяции мы можем положить F = R (не различая отдельные виды). Таким образом, поведение популяции в целом будет точно таким, как описано выше, т. е. произойдет полное вымирание за время, по порядку величины превосходящее N²/F.

Для каждого отдельного вида, однако, необходимо положить F_k < R_k, поскольку Q_k < 1; при этом снова предполагается, что все отдельные виды вырождены по отношению к F_k, R_k или Q_k. Тогда выражение (14) в табл. 10 показывает, что p₁₀ приближается к 1 для t >> 1/(R_k - F_k):

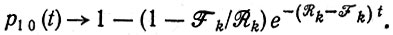(III.22)

Математическое ожидание для каждой копии уменьшается от 1 до 0:

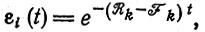(III.23)

а дисперсия стремится к

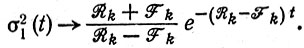(III.24)

Каждый отдельный вид вымирает. Ни один вид не сможет выжить на протяжении времени, сравнимого с временем жизни "выживших" в первом примере. Вместо этого будет наблюдаться постоянный дрейф информационного содержания вследствие ошибок воспроизведения. За свое время жизни (т. е. за время, меньшее чем N²/F) система успеет просканировать большой объем информации, не задерживаясь на воспроизведении какой-либо определенной копии в течение времени, существенно превышающего 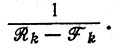Однако, как сказано выше, система в целом будет иметь ту же судьбу, что и в случае 1.

Случай 3. Устойчивый и предсказуемый отбор может наблюдаться только в том случае, если кинетические параметры изменяются в конечных пределах. Однако даже в этом случае мы имеем область "неопределенности" для отбора. Во-первых, для F > R получим математическое ожидание для растущей популяции

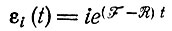
[ср. также с уравнением (III.23)]

в согласии с детерминистической теорией. Более того, для больших i при t = 0 флуктуации имеют величину порядка √i (i - начальное значение). Рассмотрим теперь равновесное распределение с W_m = E¯. Виды, обладающие конечным "селективным преимуществом" W_m+1 > W_m, имеют ненулевые, но не стопроцентные шансы быть отобранными. Согласно уравнению (14) в табл. 10, вероятность вымирания вида, если при t = 0 он был представлен k копиями, равна

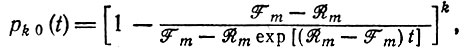(III.25)

при t → ∞

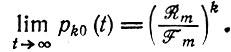(III.26)

Этот результат дает точный ответ на последний из вопросов § III.3. Если в предварительно уравновешенной популяции (т. е. в такой, что W_m = Е¯ = 0) возникнет мутант (m + 1) с селективным преимуществом (т. е. W_m+1 > W_m), то одна первоначально возникшая копия может в конце концов погибнуть с вероятностью Вероятность ее выживания равна 1 - R_m/F_m, и эта вероятность увеличивается с ростом избыточности (k) мутантных копий. Однако в линейной модели нет истинной "точки, откуда нет возврата". Вероятность вымирания для F_m+1 > R_m+1 по уравнению III.26 монотонно убывает с ростом k и приближается к нулю лишь асимптотически при больших k.

Однако мы можем определить пороговое значение вероятности как "точку полувозврата" k_¹/2 согласно условию

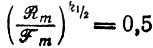(III.27)

или как соответствующую "точку релаксации" k_¹/e

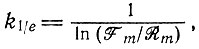(III.28)

что при условии 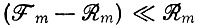дает

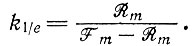(III.29)

При этом же условии 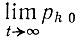может быть выражен как

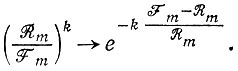(III.30)

Табл. 11 дает некоторые значения для точек релаксации k_¹/e при различных F_m/R_m. Мы видим, что мелкие селективные преимущества редко приводят к выживанию и доминированию, как это предсказывает детерминистическая теория. Этот факт еще раз подчеркивает случайный характер процессов отбора. Стохастическое выражение для частоты появления одного определенного мутанта следует умножить на (1 - lim_t→∞ р_{1 0}), чтобы получилось выражение для вероятности его макроскопического появления.

Таблица 11. Стохастический порог для выживания мутанта с селективным преимуществом F_i > R_i

Сделанные здесь выводы относятся лишь к линейным растущим системам. В настоящее время производятся расчеты для систем с ограничениями постоянных сил или потоков, а также для (реальных) нелинейных растущих систем, которые оказываются особенно интересными в связи с "нуклеацией" живых систем (см. гл. VI).

Стохастическое рассмотрение, которое существенно опирается на линейную модель рождения - гибели Бартоломея и которое сейчас распространяется на истинные стационарные состояния, приводит к некоторым важным модификациям детерминистической феноменологической теории эволюции. Оно не только подчеркивает случайную природу элементарных процессов, но и очень ясно демонстрирует, что определенные утверждения, выведенные из детерминистической теории, должны быть модифицированы для того, чтобы они правильно описывали существенные особенности эволюционных процессов.