Глава IV. Самоорганизация, основанная на комплементарном узнавании: нуклеиновые кислоты [1973 Эйген М. - Самоорганизация материи и эволюция биологических макромолекул]

§ IV.1. Истинное "самоинструктирование"

Теория отбора - имеющая довольно общий характер - до сих пор детально рассматривалась только для простых квазилинейных систем. "Квазилинейной" мы можем назвать любую систему, описываемую уравнением (II.32), например простое выражение, которое получится, если в (II.32) отбросить члены, отвечающие обратному потоку:

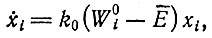(IV.1)

и в котором "селективная ценность" W_i является константой. Отметим, что ни исходное кинетическое уравнение для роста без дополнительных ограничений, ни его окончательная форма, в которой учитываются ограничения, налагаемые отбором, не может быть действительно линейным дифференциальным уравнением. Член, описывающий "образование" в исходном уравнении, содержит "стехиометрическую функцию" f_i(m₁ ... m_λ), т. е. функцию концентраций (в общем случае переменных) высокоэнергетических мономеров, точный вид которой зависит от механизма матричного процесса полимеризации, умноженную на автокаталитический член x_i. Только если высокоэнергетические мономеры забуферены согласно условию постоянной общей организации, селективную ценность можно считать постоянной в случае простого "самоинструктированного" процесса. То же условие, однако, вводит в дифференциальное уравнение функцию E, которая зависит от концентраций (т. е. содержит x_i). Таким образом, "квазилинейность" может относиться только к члену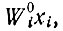

означая, что W_i теперь уже не зависит от x_i или от каких-либо x_k (которые в системе кинетических уравнений являются переменными).

При этих условиях уравнение (IV.1) описывает простейший случай истинного "самоинструктирования", т. е. образование специфичной последовательности i инструктируется самой матрицей i.

Как можно себе представить наличие процессов самоинструктирования такого типа - в качестве некоего общего явления - в природе? Мы знаем, конечно, много разных автокаталитических процессов, когда определенный продукт реакции участвует в своем собственном образовании. Однако здесь мы требуем большего: любой продукт процесса полимеризации, т. е. любая определенная последовательность, должна инструктировать образование своей собственной копии.

Простым примером может служить образование полирибоадениловой кислоты (поли-рибо А) при низких pH. Известно, что при pH ниже 4 поли-рибо А образует двухцепочечную спиральную структуру вследствие специфического спаривания протонированных остатков аденина. В отличие от структуры, постулированной Уотсоном и Криком, эта двойная спираль содержит параллельно ориентированные цепи, идущие от 3'-конца к 5'-концу. Кроме того, протонирование оснований в сущности нейтрализует отрицательные заряды фосфатных групп остова, вследствие чего эта структура более устойчива при низкой ионной силе. В других отношениях эта спираль ведет себя как структура Уотсона - Крика. Такой вывод можно сделать на основании подробных термодинамических и кинетических исследований, выполненных в нашей лаборатории [73]. Сходное явление наблюдается в случае поли-рибо Ц, где спаривание требует наличия как протонированных, так и непротонированных групп, так что существование двойной (и тройной) спирали ограничено очень узким диапазоном pH.

Во всяком случае легко можно представить себе "самоинструктирующуюся" матрицу, которая направляет синтез идентичной копии; такая система описывается кинетическими уравнениями типа (IV.1) с постоянными селективными ценностями W⁰_i. Проанализируем теперь более детально параметры A_i, Q_i и D_i, которые определяют процессы отбора и самоорганизации в системе.

Точный вид фактора усиления A_i зависит от механизма матричной полимеризации. Некоторые механизмы, в основу которых были положены стохастические модели, обсуждались Дж. Гиббсом [74].

Простейшая модель дает один и тот же временной интервал для включения каждой единицы в полимерную цепь. Если редупликация каждой цепи должна быть закончена, прежде чем может быть начата новая цепь, то постоянная времени редупликации должна расти с длиной цепи. Она пропорциональна ν (числу единиц в цепи) в начале процесса и становится пропорциональной ν², когда процесс полимеризации приближается к равновесию. Здесь вероятности прямой и обратной реакций становятся равными, так что реакция напоминает процесс простой одномерной диффузии (где время перемещения пропорционально квадрату расстояния). Для наших целей мы можем не рассматривать системы, близкие к равновесию, и это исключает возможность, что зависимость от длины цепи будет сильнее, чем линейная.

С другой стороны, существуют механизмы, которые дают значительно более слабую зависимость от длины цепи:

а) Процесс может быть кооперативным и требовать определенного времени (и определенной длины цепи) для нуклеации, которое может оказаться гораздо больше, чем время "распространения". Тогда - вплоть до некоторой "кооперативной длины" - время редупликации будет определяться временем нуклеации и, следовательно, не будет зависеть от длины. Такое кооперативное поведение имеет место, например, при узнавании оснований в процессе образования (двойной) спирали олиго-рибо А, где "длина нуклеации" равна 3, а "кооперативная длина" - примерно 30 парам оснований (при комнатной температуре).

б) Новая цепь может быть начата как на матрице, так и на реплике, прежде чем реплика будет закончена. Как хорошо известно, это явление имеет место при ферментативном считывании одноцепочечной матрицы (например, рибосомами или РНК-полимеразами), и вполне возможно, что оно происходит также при неферментативной репродукции одиночной цепи. Дж. Гиббс [74] показал, что в таком процессе множественной репродукции могут возникать "пробки" - как в уличном движении. В отличие от случая (а) зависимость от длины цепи будет здесь проявляться только для сравнительно коротких последовательностей, исчезая по достижении некоторой определенной длины.

Если объединить случаи "а" и "б", то можно получить в результате очень слабую (слабее линейной) зависимость от длины цепи, которая если и благоприятствует воспроизведению коротких последовательностей, то лишь в очень слабой степени. Могут существовать, однако, очень резкие различия в скорости для различных длинных последовательностей, потому что складывание цепи и образование петель может создать набор участков, на которых матричные эффективности будут сильно различаться. Далее, если в конкуренции участвуют различные высокоэнергетические мономерные единицы, концентрации которых различны, то единица, имеющая наибольшую концентрацию, будет включаться в цепь с большей вероятностью (поскольку это влияет на A_i и Q_i), в результате чего могут получиться очень однородные последовательности. Если в репликации участвуют ферменты^*, то в узнавании (как и в случае "нуклеации") могут участвовать специфичные участки матричной последовательности (возможно, что участвуют оба конца цепи, как в случае Qβ-репликазы; см. гл. VII).

^* (Процессы, катализируемые ферментами, можно рассматривать как "квазилинейные", если фермент (например, репликаза) представляет собой постоянный "фактор среды", т. е. не является частью "эволюционирующей" системы (см. гл. VII).)

Фактор Q_i0 накладывает более жесткие ограничения на длину цепи, чем фактор усиления, вследствие степенной зависимости

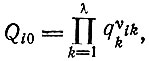(IV.2)

где индекс k относится к различным единицам 1, ..., λ. Если бы факторы узнавания отдельных единиц q_i были равны, то можно было бы применить простую модель, которая обсуждалась в табл. 8 (см. § II.5).

Как было показано, максимальное число единиц, которое может воспроизводимо копироваться, ограничено неопределенностью узнавания отдельных единиц и (слабо) зависит также от "разброса" кинетических коэффициентов. Вследствие этого, когда "единичный" (т. е. отвечающий одной единице) фактор качества равен, например, 0,99 (т. е. вероятность ошибки равна 1%), длина воспроизводимых последовательностей ограничена числом единиц ν_i порядка 100 (или даже меньше, если "разброс" 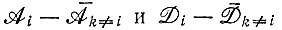близок к нулю).

Единичный фактор качества q можно выразить через свободные энергии парного взаимодействия, если узнавание является "равновесным" процессом. Рассмотрим такую стадию самоинструктированного включения мономера:

(IV.3)

представляет собой единицу матрицы, i_m - высокоэнергетическую мономерную единицу и i_p - единицу, включенную в полимерную копию; k_R, k_D и k_P - константы скорости процессов спаривания, диссоциации пар и включения единиц (полимеризации). "Равновесное" узнавание означает, что

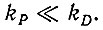(IV.4)

Измерения, описанные ниже, показывают, что кооперативное спаривание (т. е. распространение "нуклеированной" области) происходит с большой скоростью (10⁶-10⁷ с^-1), и можно принять, что k_D больше 10⁵ с^-1 (для ГЦ) или 10⁶ с^-1 (для АУ).

Предполагая "равновесное узнавание", можно записать

(IV.5)

где m_i или m_k - концентрации мономерных единиц и K_ii или K_ik - соответствующие (кооперативные) константы стабильности пары. Если равновесность узнавания не полная, то константы стабильности можно заменить на подходящие константы стационарного состояния. Константы стабильности K_ik можно выразить также через свободные энергии образования пары:

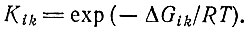
Только в том случае, когда концентрации всех мономерных единиц забуферены до одного и того же значения, все m_k сокращаются и получается простое выражение

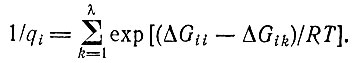(IV.7)

Как будет показано, для процессов неферментативного узнавания очень трудно получить значения единичных q-факторов, которые были бы существенно выше 0,99 (что соответствует ΔG_ik ≈ 3 ккал/моль).

Наконец, факторы разложения D_k менее важны в свете настоящего обсуждения. Скорость образования отобранного вида должна превосходить скорость разложения (W_i > 0). Что касается D-факторов, они (для неферментативных процессов) проявляют те же тенденции, что и другие факторы, т. е. не благоприятствуют длинным цепям. Если не образуется защитная макромолекулярная оболочка, длинные цепи будут гидролизоваться легче, чем короткие.

Имеются и другие аспекты, которые могут оказаться важными при обсуждении других механизмов. Однако они имеют меньшее значение по сравнению со следующим заключением об эволюции "самоинструктирующихся" кодовых систем.

Очень маловероятно, чтобы все мономеры имелись с самого начала в равных количествах. Если, с другой стороны, одна из единиц - например, адениновый нуклеотид - имеется в большом избытке, то это так сильно будет благоприятствовать ее включению при конкуренции с другими единицами, что может привести к доминированию очень однородных полимерных последовательностей (например, поли-рибо А). Такие однородные последовательности не могут кодировать, и вследствие этого такая система давала бы малые преимущества для дальнейшей эволюции самоорганизации, не говоря уже о других ее недостатках (см. ниже).

В настоящее время мы не находим в природе простого "самоинструктирующегося" кода. В принципе он мог бы существовать, но при этом он находился бы в очень невыгодном положении по сравнению с системой, использующей "комплементарное инструктирование". Такая система даже при наличии одного доминирующего мономера, имеющегося в большом избытке, немедленно стала бы накапливать другую, комплементарную единицу и строить, таким образом, смешанные системы, которые являются предпосылкой для возникновения кода.

Поможем с курсовой, контрольной, дипломной

Имя

1500+ квалифицированных специалистов готовы вам помочь

ПринимаюПолитику конфиденциальности