§ IV.2. Комплементарное инструктирование и отбор (теория)

Простая форма уравнения (IV.1) не может использоваться для описания "комплементарного инструктирования". Процесс комплементарного копирования представляет собой чередование синтезов "положительных" и "отрицательных" копий, которые мы будем обозначать +i (плюс-цепь) и -i (минус-цепь). Коллектив (±i) можно представить в виде циклического графа

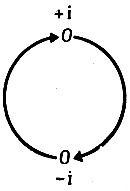
Каждый такой коллектив описывается двумя кинетическими уравнениями:

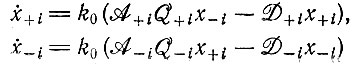(IV.8)

и два собственных значения λ будут решениями характеристического уравнения

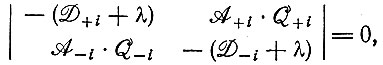(IV.9)

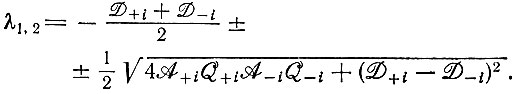(IV.10)

Эти собственные значения можно приписать определенным "нормальным координатам" реакции [75] - концентрационным параметрам y_i, которые представляют собой линейные комбинации 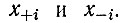Одно из значений λ всегда отрицательно, другое может быть положительным, если

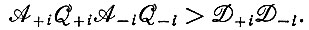
Соотношение между переменными x и y можно записать в векторной форме

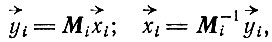(IV.11)

где матрица 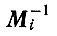обратна матрице M_i, а строится из компонент собственных векторов. Рассмотрим для простоты (более прозрачный) случай, когда 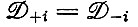(для большинства экспериментов при постоянных силах и регулируемых потоках это является хорошим приближением). Для этого случая матрицы имеют следующий вид:

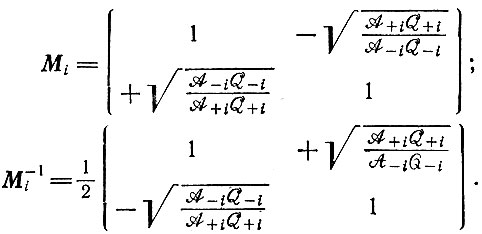(IV.12)

В том же приближении собственные значения равны

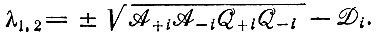(IV.13)

Физическая интерпретация состоит в том, что каждый реакционный цикл имеет два действительных собственных значения, которые определяют кинетическое поведение. Одно из них всегда отрицательно. Оно описывает релаксационный процесс "уравновешивания" при образовании плюс- и минус-цепей:

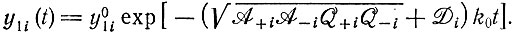(IV.14)

Релаксация приводит к постоянному отношению x_+i и x_-i. Второе собственное значение положительно, если член, описывающий усредненное значение образования 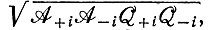превосходит член, описывающий распад 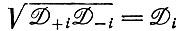(аналогично положительному W в уравнении IV.1). Оно выражает автокаталитический рост (±i)-коллектива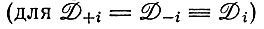

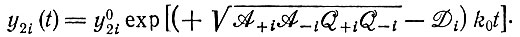(IV.15)

Эта часть решения важна для отбора. Матрицы M_i и ^M-1_i позволяют перейти от "нормальных" к истинным концентрациям или наоборот; например, в том случае, когда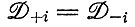

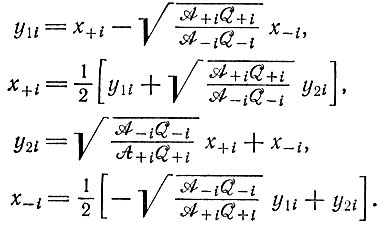(IV.16)

Так как y_1i → 0 при t → ∞, "уравновешенное" отношение 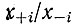равно

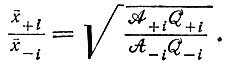(IV.17)

Для равных скоростей образования плюс- и минус-цепей это отношение равно единице. Если процесс начинается с уравновешенного отношения (при t = 0), то имеет место только одно решение, т. е. рост 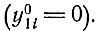В более обычном случае (см. эксперименты с фагом Qβ, описанные в гл. VII) процесс начинается с одной копии, например с плюс-цепи 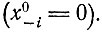Тогда изменение во времени каждого вида складывается из обоих решений, пока не достигается постоянное отношение, после чего решение роста доминирует.

Введем теперь в кинетические уравнения давление отбора (ограничение постоянной общей организации):

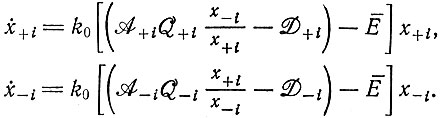(IV.18)

Сразу видно, что эти уравнения относятся к тому общему типу, который обсуждался в гл. II, поскольку отношение (x_+i/x_-i) или обратное отношение не исчезает с ростом t.

Обозначим это отношение 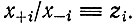Из (IV.18) немедленно следует дифференциальное уравнение для изменения z во времени:

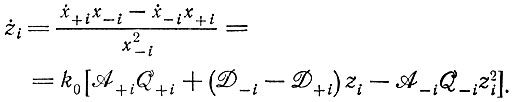(IV.19)

В результате интегрирования получаем довольно громоздкое выражение

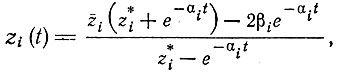(IV.20)

где

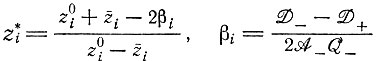
и

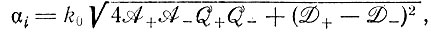
которое при t = 0 дает начальное значение z⁰_i и при t → ∞ уравновешенное отношение

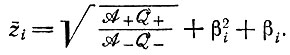(IV.21)

Подстановка z_i(t) в (VI.18) приводит к неоднородному дифференциальному уравнению, которое можно проинтегрировать.

Общее поведение системы с комплементарной инструкцией аналогично поведению "самоинструктирующейся" системы, которое обсуждалось выше. Каждый коллектив, несущий информацию, теперь состоит из двух компонентов и может быть представлен двухкомпонентным вектором 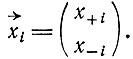Прежняя величина 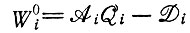теперь заменяется матрицей

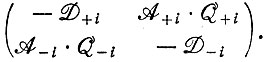
Эта матрица имеет два собственных значения, одно из которых относится к уравновешиванию коллектива (±i), а другое описывает свойство конкурентного роста этого коллектива. Следовательно, это собственное значение и соответствующая ему нормальная координата (y_2i) входят в уравнение для отбора. После уравновешивания коллектива мы можем заменить нормальную координату y_2i просто суммой 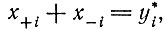оба члена которой пропорциональны y_2i, и затем записать в обычной форме уравнение отбора при постоянных силах

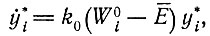(IV.22)

где 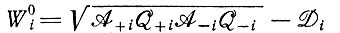(предполагая, что 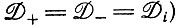и

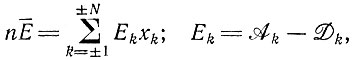
где суммирование распространяется на все + и - k.

При 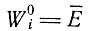получим селекционное равновесие, в котором (снова при условии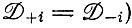

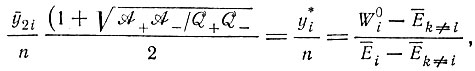(IV.23)

где

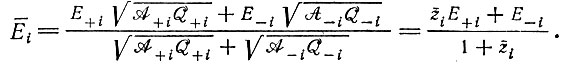
(В случае 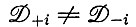это выражение сохраняет свой общий вид, но W⁰_i и E_i должны быть вычислены согласно уравнению (IV.10) при помощи полных матриц преобразования M_i и M^-1_i).

Можно видеть, что до тех пор, пока 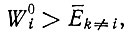отбор (±)-коллектива происходит даже в том случае, если для одной из копий (например, для -i) значение Е меньше, чем Е¯_k≠i. Различные коллективы i_i снова подвергаются отбору. При отсутствии других связей между различными i_i выживает только один коллектив i_m (вместе с его "кометным хвостом" ошибок), т. е. тот, который имеет максимальную селективную ценность W⁰_m > 0 (или вырожденная группа коллективов). Селективная ценность коллектива содержит среднее геометрическое параметров для плюс- и минус-цепей. Этот интересный результат показывает, что параметры воспроизведения обеих цепей одинаково важны. (Отметим, что среднее арифметическое было бы эквивалентно члену, "лимитирующему скорость".) В настоящем случае более медленный компонент дорастает до большей стационарной концентрации и тем самым достигает скорости быстрого компонента.

Важная особенность "комплементарного инструктирования" состоит в том, что даже при большом избытке одного мономера система всегда должна накопить по меньшей мере два различных мономера, которые затем встречаются у отобранного вида в почти равных количествах. Тогда вследствие копирования ошибок система будет всегда образовывать смешанные последовательности. Это служит предпосылкой для возникновения любого кода, который может приобрести "смысл" ("представляя" информацию, которая поддается оценке) в том случае, если каждая из смешанных последовательностей дает селективное преимущество для своего собственного воспроизведения. Как мы увидим дальше, бинарные кодовые системы с самого начала имеют определенные преимущества, не препятствуя в то же время переходу к высшей (например, четверной) форме кода, если это почему-либо выгодно. Вследствие конкурентной природы отдельных (±i)-ансамблей количество информации, которое может храниться, ограничено емкостью одного-единственного класса носителей (т. е. главной копии с ее постоянным "кометным хвостом" ошибочных копий) иди емкостью вырожденной группы. Следовательно, ограничения, налагаемые на длину, которые определяются в основном факторами качества Q_+i и Q_-i являются важными. Информацию о комплементарном узнавании оснований нуклеиновых кислот можно получить из экспериментальных данных.