§ VI.2. Самовоспроизводящийся гиперцикл

VI.2.1. Модель. Рассмотрим простую модель, изображенную на рис. 16. Она состоит из ряда нуклеотидных последовательностей (или, лучше, (±)-коллективов) I_i с ограниченной длиной цепи. Эти коллективы не должны содержать больше информации, чем требуется для кодирования одной или двух каталитически активных полипептидных цепей, которые мы обозначим Е_i. Кружок вокруг I_i условно представляет способность нуклеотидного коллектива к комплементарному инструктированию, а каждый такой коллектив состоит из "положительной" и "отрицательной" цепей, взаимно воспроизводящих друг друга. Этот процесс воспроизведения специфично катализируется предшествующей полипептидной цепью E_i-1.

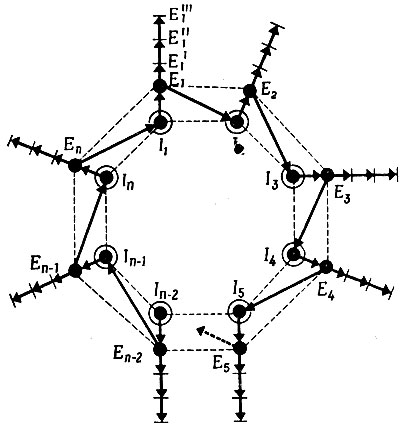
Рис. 16. Самоинструктирующийся каталитический гиперцикл. I_i - носители информации, т. е. комплементарные цепи РНК. Каждый черный кружок обозначает самоинструктирующее свойство коллектива I_i, содержащего две комплементарные цепи. Е_i (кодируемый I_i) - каталитическая функция. Каждая ветвь Е_i может выполнять несколько функций (например, полимеризацию, трансляцию, регулирование), одна из которых должна обеспечивать связь с носителем информации I_i+1 (например, катализировать образование I_i+1 путем специфичного узнавания). Контур, включающий в себя все связи, должен быть замкнут, т. е. должна существовать такая Е_n, которая катализирует образование I₁. Гиперцикл описывается системой нелинейных дифференциальных уравнений

Полипептидная цепь E_i-1 кодируется нуклеотидной цепью I_i-1. Наличие транслирующей системы обеспечивает достаточно точную передачу информации от I_i к E_i. Только часть информации, хранящейся в каждом I_i, должна использоваться для кодирования функции, которая усиливает образование следующего носителя информации; вся остальная Информация может использоваться для кодирования общих ферментативных функций, таких, как трансляция, полимеризация, регуляторные функции и т. д. Далее каждый из Е_i, функция которого состоит в том, чтобы специфично усиливать образование следующего носителя информации, может (но не должен) представлять собой специфичную полимеразу (как, например, Qβ-репликаза, см. гл. VII). E_i может быть также специфичным индуктором (или дерепрессором), действующим на общую полимеразу. Важно, чтобы весь "гиперцикл" был замкнут, т. е. чтобы существовал такой Е_n, который действует на I₁. Таким образом, система представляет собой "циклическую иерархию", в которой многие циклические (комплементарные) коллективы нуклеотидов связаны вместе посредством ферментативного "гиперцикла". Наличие этой вторичной замкнутой петли важно потому, что в противном случае различные I_k стали бы не кооперировать, а конкурировать и вытеснять друг друга.

Эта система имеет ряд свойств, которые ниже обсуждаются более подробно:

1. Каждый цикл (подобно системам, рассмотренным в гл. IV и V) способен к автокаталитическому росту.

2. Независимые циклы конкурируют и подвергаются отбору.

3. Вследствие нелинейности отбор очень жесткий, и если имеются особые точки, то действие отбора происходит практически по типу "все или ничего".

4. Обладая этими селективными свойствами, система способна, во-первых, использовать очень малые селективные преимущества (вероятность возникновения которых должна быть стохастически значима) и, во-вторых, очень быстро эволюционировать; отобранная система не будет толерантна к возникновению независимых конкурентов, поэтому код и хиральность будут универсальны.

5. Циклические связи обеспечивают информационную емкость, приспособленную к требованиям системы. Тем не менее репликационная длина отдельной кодирующей единицы (см. оценку v в табл. 8) должна быть достаточно мала, чтобы обеспечить воспроизводимость.

6. Система может эволюционировать, т. е. совершенствоваться, путем использования селективных преимуществ. "Генотипические" мутации, т. е. изменения в I_i, могут немедленно использоваться E_i-1 и не должны ждать, пока произойдет коррелированная серия мутаций для того, чтобы распространиться по циклу, как это было необходимо для "линейных" каталитических циклов (см. гл. V). Селективные преимущества могут проявляться через репрессию, дерепрессию или промотирование.

7. В системе происходит отбор против паразитных ветвей, если селективные ценности последних ниже, чем для членов цикла. Паразитные ветви с высокими селективными ценностями не дадут возможности циклу пройти стадию нуклеации, если они имеются с самого начала. Однако если эти ветви появляются после того, как цикл прошел стадию нуклеации, то вследствие нелинейного селекционного поведения они не имеют шансов расти. Цикл может сжаться, т. е. сократить число своих членов, если это дает какое-либо селективное преимущество. Условия одновременного существования нескольких связанных циклов очень ограниченны.

8. Существует только один тип ветвей, которые могут сосуществовать с циклом; это ветви, селективные ценности которых точно совпадают с селективной ценностью цикла. Точное совпадение возможно только в том случае, если ветвь и кодирующий участок I_i внутри цикла используют "один и тот же промотор, локализованный в E_i-1. Это автоматически приведет к генной и оперонной структуре кодовой системы. В области ветвей у системы могут развиться функции "общего пользования" (например, функции, выполняемые полимеразами, системой трансляции, регулирующими факторами, метаболическими ферментами).

9. Вскоре после нуклеации система должна пространственно обособиться от среды. Только компартментализованные системы могут использовать функциональные ветви (возникшие вследствие мутаций) исключительно на свою собственную пользу (одновременно создавая возможность для эволюции ветвей). При помощи того же механизма система спасается от "загрязнений", вызванных неблагоприятными мутациями в ветвях.

10. Система, обособившаяся от среды, может "индивидуализироваться" путем соединения своих кодирующих единиц в стабильную цепь, например с помощью (эволюционирующей) лигазы, и воспроизводить всю эту цепь как индивидуальную единицу. В такой цепи (которая при участии лигаз будет циклической) гены, происходящие от данной единицы I_i, должны располагаться в соседних положениях. Однако матрица, кодирующая связывающий фактор и происходящая из I_i-1, может находиться на довольно значительном расстоянии.

Последние два пункта, очевидно, не представляют собой неотъемлемые свойства цикла. Они показывают, что цикл не является "тупиком" в отношении дальнейшей эволюции. Он способен использовать любые преимущества, что приводит его к такому уровню сложности, который близок к сложности живой клетки. Или, другими словами, лишь те системы, которые сумели компартментализоваться и обособиться, получили в конце концов шансы на выживание.

VI.2.2. Теоретическое рассмотрение. Теория циклической системы, описанной выше, разработана нами вместе с П. Шустером. Вычисления сделаны на ЭВМ. Подробности этой работы будут опубликованы позднее [100]. В этом параграфе кратко излагаются лишь некоторые предварительные результаты.

Рассмотрим сначала простой предельный случай нелинейных кинетических уравнений, дающий конструктивное представление о том, какой тип решений следует ожидать. Если белки находятся в квазиравновесии со своими кодирующими единицами I_i, то мы можем не рассматривать в явном виде скорости их образования и можем считать, что их концентрации пропорциональны y_k - концентрациям инструктирующих кодовых единиц I_k (которые здесь мы считаем просто "самоинструктирующимися"). Если, далее, из пары концентраций E_i-1 и I_i ни одна не имеется в большом избытке, и, следовательно, можно принять, что концентрация комплекса между E_i-1 и I_i пропорциональна произведению обеих концентраций (соответствуя области второго порядка в модели Михаэлиса - Ментен), то кинетические уравнения для образования кодирующих единиц - без ограничений, налагаемых отбором, - можно записать следующим образом:

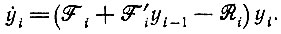(VI.1)

(Снова предполагается, что концентрации всех высокоэнергетических мономеров забуферены. Члены, описывающие "обратный поток", также не учитываются.)

Решение этого уравнения - как и уравнения (II.21) - имеет особую точку при конечном t (при условии, что 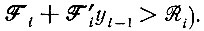Это иллюстрирует рис. 17. Интересно отметить, что для циклов с тремя и более членами могут возникнуть колебания. Эти колебания еще более выражены при наличии налагаемых отбором ограничений (см. рис. 18). Двучленные циклы не дают колебаний; при трех членах колебания есть, но они затухают; при четырех и более членах затухание исчезает. Если начать с независимых от времени средних (соответствующих внутреннему равновесию), то колебания возникают после малого возмущения. Независимые от времени средние можно получить из стационарного решения (внутреннее "равновесие")

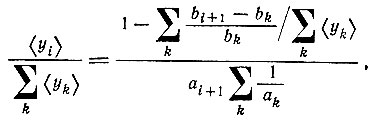(VI.2)

где сумма распространяется на все k членов цикла, 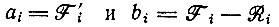согласно уравнению (VI.1). Символ 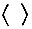для осциллирующих концентраций означает среднее по времени.

Рис. 17. Рост четырехчленного гиперцикла (4 носителя информации кодируют 4 фермента сопряжения E_i). Предполагается, что при t = 0 имеется 10-кратный избыток I₁ по сравнению с I₂, I₃ и I₄. Скорости образования для всех четырех членов сводятся к простому выражению второго порядка х_iх_i-1. Разложение не учитывается. Ось времени трансформирована и относится к константе скорости k = 1 (или t = kt'). Существование особой точки при t = 7,3 приводит к очень резкому отбору, если имеется несколько конкурирующих циклов. (Вычисления П. Шустера [100].)

При увеличении числа k кодирующих единиц осциллирующее поведение проявляется в виде волн с пиками характерной формы, которые обегают вокруг цикла. Форма этих пиков зависит как от k, так и от относительных скоростей образования и распада отдельных кодирующих единиц (см. рис. 18-21). Селекционное поведение конкурирующих циклов зависит не только от среднего кинетического параметра цикла, но и от относительных скоростей отдельных этапов и их распределения между различными этапами, а также от k - числа кодирующих единиц в цикле (рис. 22-24). Держать пари о результате такой конкуренции оказывается так же трудно и почти так же увлекательно, как играть на скачках. Обсуждение деталей реакционных механизмов выходит за рамки этой работы (это можно найти в другом месте). То же самое справедливо для поведения связанных циклов, свойства которых во многом напоминают социальное поведение.

Рис. 18. Решения, описывающие отбор k-членных гиперциклов при ограничении постоянной общей организации (k = 2, 3, 4, 5, 6, 12). Скорость образования снова описывается простым выражением второго порядка - одинаковым для всех членов цикла (ср. рис. 17), скорость 'удаления' - членом первого порядка, чтобы выполнялось условие Σ_kх_k = const. Показаны решения только для одного члена цикла. Для k ≤ 3 существуют постоянные 'равновесные' значения; для k = 3 система приближается к селекционному равновесию, совершая затухающие колебания; для k > 3 возникают устойчивые колебания. Это можно показать, если, отправляясь от постоянного распределения, при t = 0 создать малое возмущение. При этом устанавливается колебательный режим. (Вычисления П. Шустера [100].)

Рис. 18. Продолжение. Решения, описывающие отбор k-членных гиперциклов при ограничении постоянной общей организации (k = 2, 3, 4, 5, 6, 12). Скорость образования снова описывается простым выражением второго порядка - одинаковым для всех членов цикла (ср. рис. 17), скорость 'удаления' - членом первого порядка, чтобы выполнялось условие Σ_kх_k = const. Показаны решения только для одного члена цикла. Для k ≤ 3 существуют постоянные 'равновесные' значения; для k = 3 система приближается к селекционному равновесию, совершая затухающие колебания; для k > 3 возникают устойчивые колебания. Это можно показать, если, отправляясь от постоянного распределения, при t = 0 создать малое возмущение. При этом устанавливается колебательный режим. (Вычисления П. Шустера [100].)

Рис. 19. Изменение амплитуды колебаний в гиперцикле [100]. Колебания возникают из постоянного стационарного распределения при

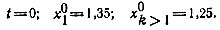
Рис. 20. Снижение амплитуды в линейном каталитическом цикле (см. гл. V) для сравнения с рис. 19. При наложении ограничений, обусловленных отбором, концентрации всегда приходят к постоянному стационарному уровню (см. [100])

Рис. 21. Стационарные колебания в уравновешенном четырехчленном гиперцикле с несимметричным распределением скоростей [100]. Константа скорости образования 4-го члена в 10 раз меньше, чем для всех других членов гиперцикла

Рис. 22. Конкуренция между двумя 4-членными гиперциклами, у одного из которых константы скорости образования на 10% меньше, чем у другого: F'₁₁ = F'₁₂ = F'₁₃ = F'₁₄ = 1,0; F'₂₁ = F'₂₂ = F'₂₃ = F'₂₄ = 0,9 (ср. [100])

Рис. 23. Конкуренция между трех- и четырехчленным циклами, имеющими одинаковые индивидуальные кинетические параметры, но различающимися по начальным концентрациям [100]. Трехчленный цикл 'побеждает'. Для трехчленного цикла 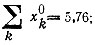для четырехчленного - 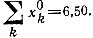Отметим, что концентрация каждого вида молекул, участвующих в четырехчленном цикле, примерно на 15% меньше, чем концентрация молекул в трехчленном цикле

Рис. 24. Конкуренция между трех- и четырехчленным циклами, которые имеют одинаковые индивидуальные кинетические параметры, но различаются по начальным концентрациям [100]. Для трехчленного цикла 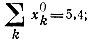для четырехчленного 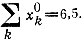Отметим, что здесь побеждает четырехчленный цикл, хотя концентрация каждого вида входящих в него молекул и в этом случае меньше, чем концентрация молекул в трехчленном цикле

Более полное решение должно учитывать следующие усложнения:

1. Система Е_i, хотя она и связана с I_i, имеет свои характерные скорости роста. Следовательно, необходимо ввести два набора концентрационных переменных: x_i - для ферментов Е_i и y_i - для кодирующей системы I_i.

2. Скорость редупликации носителей кода не пропорциональна произведению х_i-1y_i. Приближение Михаэлиса - Ментен (в котором предполагается большой избыток субстрата над ферментом) не удовлетворительно. Концентрации комплексов между Е_i-1 и I_i, обозначаемые z_i, следует вычислять на основании закона действия масс. Их можно представить в виде

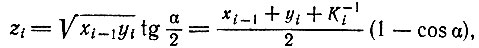(VI.3)

причем

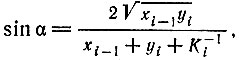(VI.4)

где x_i-1 и y_i - полные концентрации E_i-1 или I_i соответственно (независимо от того, свободны они или связаны в комплексе) и K_i - константа стабильности комплекса между E_i-1 и I_i.

3. Скорость образования I_i включает два члена: линейный член и член, пропорциональный z_i. Всегда имеется какое-то воспроизводимое образование I_i, происходящее без специфического содействия E_i-1. Если бы мы имели только член второго порядка, нуклеация цикла была бы очень маловероятным процессом.

4. Связанные системы кинетических уравнений можно записать следующим образом^*:

^* (Различение концентраций свободных [(y_i - z_i) или (x_i - z_i) соответственно] и связанных (z_i) молекул не изменило бы общего вида этих уравнений, потому что в них входят члены, пропорциональные как y, (или x_i), так и z_i.)

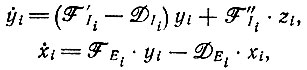(VI.5)

где z_i дается уравнением (VI.3).

Решение (полученное при ограничениях постоянной общей организации) имеет область второго порядка - как обсуждалось выше - с совершенно аналогичными свойствами; оно выполняется при условии

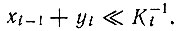
Если одна из концентраций превышает 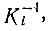решения становятся квазилинейными и колебания исчезают, но это происходит в общем случае уже после того, как система подвергалась резкому отбору при прохождении через нелинейную область. Дальнейшие подробности см. [100].

Выводы теории, относящиеся к селекционному поведению конкурирующих циклов, можно суммировать следующим образом. Под действием ограничений, налагаемых отбором, различные гиперциклы конкурируют друг с другом. Выживает только одна система, характеризующаяся максимальной функцией ценности, которая имеет очень сложный вид и может быть выражена через параметры скорости и качества, а также через средние концентрации членов цикла. Концентрации отдельных членов могут осциллировать, пока система проходит через нелинейную область. Отбор очень жесткий и этим объясняется единственность кода и хиральности. Всякий раз, когда зарождается цикл, выбирая определенный код и аппарат трансляции (см. § VI.3) - а он должен это сделать, чтобы воспроизводить свои функциональные свойства, - жесткий отбор приводит к универсальному использованию этого конкретного кода, потому что новые циклы не могут сосуществовать с первым, после того как он стабилизировался. То же самое верно для хиральности. После того как полимеризующие функции избрали данную стереохимическую конфигурацию, этот выбор будет сохраняться и эволюционировать до совершенства, которое требует однородной стереоспецифичности. Хотя a priori обе конфигурации равновероятны, одна из них, которая в результате флуктуаций случайно имелась в наличии в момент нуклеации, впоследствии всегда остается предпочтительной вследствие нелинейного усиления. Для нелинейных систем "с селекционным поведением типа "все или ничего" только один вид может победить. Это не обязательно относится к тем функциям, которые не участвуют в нелинейной связи. Например, олигопептиды, которые не производятся биосинтетическим аппаратом, использующим закодированные сообщения, могут содержать также D-аминокислоты (например, грамицидин S, см. гл. V).

Нелинейность является также причиной отбора против паразитных ветвей, которые не могут расти после того, как произошла нуклеация стабильного гиперцикла, если только они не являются частью какой-либо единицы, кодируемой этим циклом. Колебательное поведение цикла добавляет новые особенности - прежде всего в отношении жесткости отбора. Различные члены цикла воспроизводятся в виде волн, обегающих вокруг цикла, и отбор заканчивается после того, как эти волны сделают всего несколько оборотов (рис. 22). Такое поведение делает затруднительным сосуществование связанных гиперциклов - если только не возникают связи совершенно особого типа (см. [100]).

Возникновение гиперцикла зависит от наличия аппарата трансляции (см. § VI.3), причем процесс нуклеации основывается на статистике того же типа, что и для линейных циклов [см. § V.3, уравнения (V.14)-(V.16)]. Однако в отличие от циклических белковых сетей гиперцикл может эволюционировать и тем самым оптимизировать свое функционирование. Во-первых, он не разветвлен, как линейная сеть, рассмотренная в гл. V; во-вторых, он может использовать селективные преимущества, появляющиеся внутри цикла, в той мере, в какой они создают преимущество для воспроизведения генотипической мутации. Такая эволюция может также приводить к сжатию цикла до оптимальных размеров. Эти размеры должны обеспечивать достаточно большую информационную емкость, включая все вспомогательные функции, такие, как полимеризация, трансляция и регулирование (а позже - и более сложные метаболические функции). Определенное преимущество дает объединение различных единиц I_k в коллектив, имеющий относительно большую информационную емкость, Отдельная единица может кодировать только две функции: узнавание - для того чтобы обеспечить циклическую связь с помощью системы E_k - и (иногда) вспомогательную функцию (т. е. трансляцию или полимеризацию). Если все функции, которыми обладает данный цикл, должны быть закодированы в одной непрерывной молекуле нуклеиновой кислоты, то с самого начала необходима очень большая точность узнавания (т. е. очень хорошо адаптированные ферменты), иначе все это количество информации не сможет стабильно воспроизводиться; информация будет утекать до тех пор, пока вся полезная информация не будет утрачена.

С другой стороны, если цикл уже выработал достаточно точную систему узнавания, то наличие лигазы, сшивающей различные единицы в одну воспроизводящуюся цепь, дает определенные селективные преимущества. Это могло быть тем моментом, когда эволюция структур из ДНК стала давать преимущества по сравнению с одноцепочечными структурами из РНК. "Обособление" гиперцикла, который тем самым становится истинной "самовоспроизводящейся" системой, следует рассматривать в связи с "компартментализацией". Ни "обособление", ни "компартментализация" не принадлежат к числу неотъемлемых свойств гиперцикла (в отличие от других свойств, упоминавшихся выше). Однако, если они появляются после нуклеации, они могут создать селективное преимущество и, таким образом, представляют собой неизбежное следствие эволюции гиперцикла. Преимущества состоят в использовании мутаций. Мутации, особенно мутация, затрагивающая вспомогательную функцию, оказавшаяся благоприятной, будет использоваться всей "диспергированной" системой и, таким образом, не будет специально благоприятствовать воспроизведению мутанта, если только она не возникла внутри отдельного "отсека". В последнем случае мутация будет благоприятствовать только одной этой системе, которая после обособления будет успешно конкурировать со своими предшественниками. То же самое справедливо для неблагоприятных мутаций, которые, если они возникают в отдельном "отсеке", будут оказывать действие (или даже разрушать) только на этот "отсек" и, таким образом, исчезнут, тогда как в противном случае они могли бы засорить всю систему.

Подходящими "отсеками" могли бы быть коацерваты, впервые описанные А. И. Опариным [101], или микросферы, состоящие из липидов, или протеиноиды (имеющие в основном гидрофобные боковые цепи); последние, как было показано С. Фоксом [102] и другими, могут спонтанно образовываться в условиях, которые могли способствовать конденсации аминокислот и которые, вероятно, существовали на примитивной Земле.

Липидные микросферы встречаются очень часто, как было показано различными авторами. Их можно воспроизводимо получить и использовать в лабораторных экспериментах [103-106].