19. Игра жизни: второй закон Менделя

Представим себе карточную игру, в которой участвуют три игрока. Один из них - отец, другой - мать, третий - ребенок. В начале игры у матери и отца одинаковое количество карт, а у ребенка ни одной. Игра заключается в том, что ребенок набирает в руки карты по определенным правилам.

1. Первое правило гласит, что находящиеся в одних руках карты всегда парные: два туза, два короля и т. д. В отношении масти никаких ограничений нет. Так, например, все четыре короля отца и матери могут быть пиковыми, или отца оба пиковые, а у матери червовые, или все четыре короля могут быть разной масти и т. д.

2. Второе правило предписывает, чтобы ребенок вытягивал наудачу карты по одной, и только по одной, из каждой пары карт на руках у отца и у матери.

3. Третье правило требует, чтобы все делалось независимо для каждой пары. Если, например, отец выставил карты в ряд, а ребенок выбрал из первой пары левую карту, он может в следующей паре выбрать либо правую, либо левую, и так для всех пар.

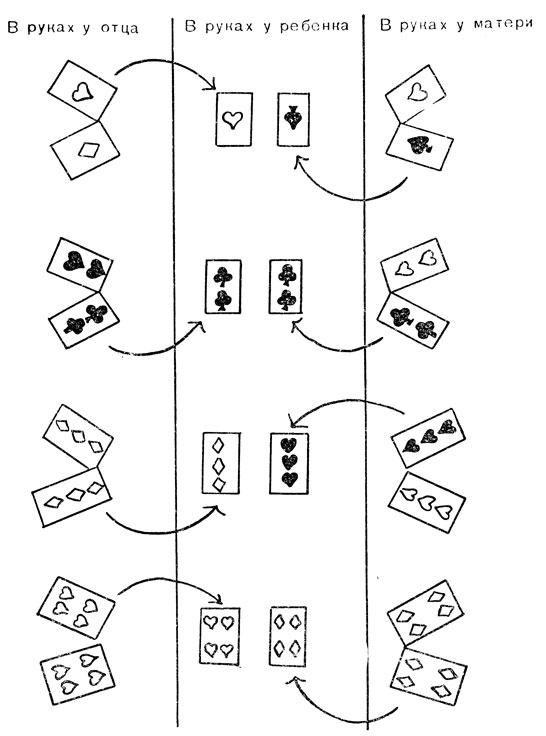
Рис. 59. В карты играют отец, мать и ребенок

Рис. 59 показывает результаты такой игры для четырех пар карт. Комбинация карт на руках ребенка, полученная в этой игре, только один из многих возможных вариантов. Вместо того чтобы вытащить туза червей от своего отца и туза пик от матери, он мог вытащить другие карты или от одного, или от обоих родителей. Так, он мог получить два туза червей, или один туз червей и один туз бубен, или один туз пик и один туз бубен. Точно так же вместо двух трефовых двоек он мог вытащить трефовую двойку вместе с червовой, или двойку пик с двойкой червей, или двойку пик с Двойкой треф. В общем имеется четыре комбинации из Двоек, которые с равными шансами можно вытянуть. Так как в соответствии с третьим правилом игры двойки вытягивают независимо от того, какие тузы были вытянуты, каждая из четырех комбинаций из двоек может сочетаться с каждой из четырех возможных комбинаций тузов. Это создает уже 16 возможных сочетаний карт, если принять во внимание только тузы и двойки. Вытягивание троек может привести только к двум комбинациям, потому что у отца тройки одной масти. Так как каждая комбинация троек может сочетаться с 16 комбинациями тузов и двоек, то создается уже 32 сочетания карт, которые с равными шансами можно вытянуть. Это число остается неизменным при последнем вытягивании, потому что четверки могут дать только один вариант.

Очевидно, что получится большее число комбинаций, если игру вести с большим числом карт. В природе, где в игре вместо карт участвуют хромосомы, обилие возможных комбинаций является одним из главных источников неисчерпаемого разнообразия живых существ. Теперь мы рассмотрим путь, которым природа осуществляет правила игры с хромосомами.

Для этого мы прежде должны вернуться к первым глазам этой книги, где говорилось о мейозе и образовании гамет. Вспомним, что во время мейоза партнеры хромосомных пар расходятся в разные гаметы. Этот процесс (в отношении одной пары хромосом - см. рис. 3) служит основой первого закона Менделя. Он объединяет два правила нашей карточной игры:

1) хромосомы сгруппированы в пары, подобно игральным картам в нашей игре;

2) при оплодотворении ребенок получает одну, и только одну, хромосому от каждой родительской пары: какую именно - дело случая;

3) третье правило вступает в силу, когда рассматривается больше одной пары хромосом.

Каждую родительскую хромосому можно отнести в одну двух групп. Первая группа - отцовские, получены через сперматозоиды; другая - материнские, через яйцеклетку. С точки зрения ребенка каждый родитель несет в себе группу хромосом от бабки и группу хромосом от деда. Третье травило игры в передачу хромосом можно выразить следующим образом: от каждого родителя ребенок получает случайный набор хромосом деда и бабки. Если, например, среди хромосом, полученных от отца, номер один принадлежал дедовскому набору хромосом, то номер два имеет равные шансы принадлежать к дедовскому или бабкиному набору хромосом, и так по отношению ко всем хромосомам, полученным от каждого родителя.

На рис. 60 показан механизм, с помощью которого это осуществляется. Здесь дано крайне упрощенное изображение мейоза и процесса образования гамет у мужчин с двумя парами хромосом. Одну группу хромосом (на рисунке зачернена) будем считать отцовской. Перед тем как разделиться, хромосомные пары сходятся в середине клетки (I). Их взаимное расположение на этой стадии определяет путь, по которому они потом будут распределены по гаметам. Для двух хромосомных пар возможны два пути разделения, вероятности которых одинаковы, они представлены на диаграммах как IIa и IIb и III. Это приводит к появлению двух наборов гамет (IV), причем каждый набор состоит из двух дополнительных комбинаций хромосом. Так как вероятности появления наборов равны, в достаточно большом количестве сперматозоидов все четыре возможные комбинации будут встречаться одинаково часто. При формировании яйцеклетки наблюдается тот же процесс, но из каждого набора четырех гамет только одна выживает и развивается в яйцеклетку. Но так как это дело чистейшей случайности, какая именно гамета выживет, конечный результат будет тот же, что и у мужского пола: в большинстве яйцеклеток все четыре возможные комбинации хромосом будут представлены в равном числе.

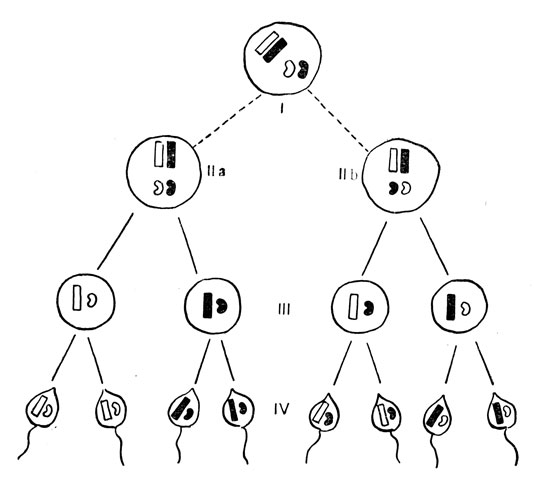
Рис. 60. Мейоз двух пар хромосом

Так как каждый из четырех типов сперматозоидов имеет равные шансы оплодотворить яйцо каждого типа, у ребенка одинаковые шансы получить одну из 16 возможных комбинаций двух хромосомных пар, подобно тому как в карточной игре у него равные шансы получить какую-нибудь одну из 16 возможных комбинаций из двух пар карт.

Гены вынуждены следовать за хромосомами, и поэтому способ, по которому гены различных хромосом комбинируются в последующих поколениях, привел Менделя к открытию второго закона, "закона независимого распределения", или "закона свободной рекомбинации". На современном языке закон формулируется так: при образовании гамет гены из различных хромосомных пар расходятся независимо друг от друга, и у потомков можно обнаружить всевозможные комбинации из них. Этот закон соответствует нашему третьему правилу игры, которое устанавливает, что вытягивание каждой пары карт производится независимо от того, как были вытянуты остальные пары. Применяя это правило, можно разобраться в наследовании многих генов той же самой родословной. Проиллюстрируем этот метод несколькими примерами.

Сперва ознакомимся с одним вошедшим в историю опытом с горохом, на основании которого Мендель вывел свой торой закон. Вместо того чтобы проследить проделанный им трудный путь от полученных данных к лежащему в их основе закону, вступим на более легкий путь и покажем, то закон в самом деле позволяет предвидеть результаты проведенных Менделем опытов. В опыте, о котором идет речь, Мендель использовал сорта гороха, которые отличались друг от друга не по одному признаку, а по двум, и зачем проследил, каким образом эти признаки комбинируются в потомстве. Один сорт характеризовался гладкими желтыми семенами, тогда как у другого сорта семена были морщинистые и зеленые. Мы уже знаем: гладкость семян зависит от наличия гена R, который является доминантным над рецессивным аллелем r-геном морщинистости семян (см. гл. 6). Мы также знаем, что произойдет, если скрестить растение гладкосемянного сорта с растением из морщинистосемянного сорта (см. рис. 13): все семена первого гибридного поколения будут гладкими; после их высева и самоопыления второе поколение семян распадется на ³/₄ круглых и ¹/₄ морщинистых. Также Мендель установил, что желтая окраска семян зависит от гена Y, доминирующего над рецессивным аллелем y, дающим зеленую окраску семян. При скрещивании растений с желтыми семенами и растений с семенами зелеными первое поколение семян получится желтым; если семена вырастить, скрестить выросшие растения и самоопылить, второе поколение семян расщепится/ на две группы: ³/₄ желтых и ¹/₄ зеленых. Эти две пары генов находятся на разных парах хромосом, и поэтому к ним применим второй закон Менделя. Сущность его заключается в том, что оба расщепления совершенно независимы друг от друга, как независимы два последовательных выхода карт в нашей карточной игре. Предположим, что мы рассортировали сперва горошины на ³/₄ гладких и ¹/₄ морщинистых. В таком случае, согласно второму закону Менделя, расщепление на классы окраски должно быть одинаковым как среди гладких, так и среди морщинистых. Конечные результаты во втором поколении будут таковы:

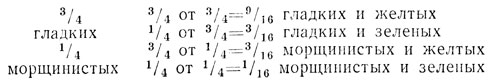
Мендель как раз получил такие результаты, и они позволили ему открыть закон независимого расхождения, или свободного перекомбинирования. Надо особо отметить, что во втором поколении получено четыре различных типа горошин; в дополнение к исходным двум типам, круглым желтым и морщинистым зеленым, появилось два новых типа: круглые зеленые и морщинистые желтые.

Свободное перекомбинирование по закону Менделя представляет собой главный источник наследственной вариации в природе и является основой многочисленных устремлений селекционеров растений и животных соединить в одной породе или сорте данные качества ряда других.

Второй пример (рис. 61) взят из генетики человека. Сделано упрощенное допущение, что разница между карими и голубыми глазами, курчавыми и прямыми волосами зависит от отдельных пар генов, причем ген карих глаз (●) доминирует над генами голубых глаз (○), а ген курчавых волос (SS) доминирует над геном прямых волос (||). Предполагается, что отец и мать гетерозиготны по генам курчавых и прямых волос и поэтому фенотипично имеют курчавые волосы. У отца глаза карие, но он гетерозиготен по "голубому" гену. У матери голубые глаза, и она гетерозиготна по "голубому" гену. Половые хромосомы отца X и Y, а матери X и X. Каковы шансы, что их ребенок будет мальчиком или девочкой с одной из четырех возможных комбинаций окраски глаз и характера волос: карие глаза и курчавые волосы, карие глаза и прямые волосы, голубые глаза и курчавые волосы, голубые глаза и прямые волосы?

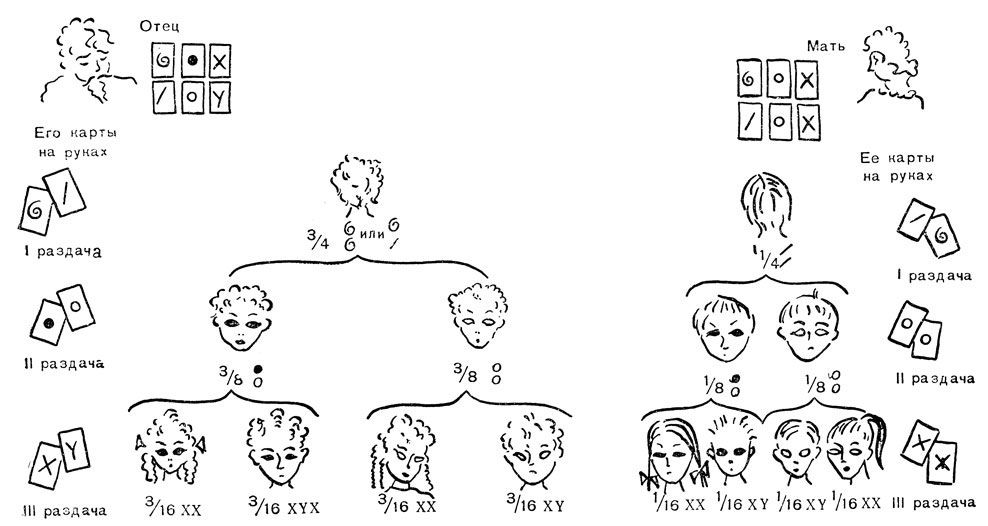
Рис. 61. Игра в гены вместо игры в карты

На рис. 61 гены и половые хромосомы представлены в виде игральных карт, и мы получим ответ на наш вопрос, применив правила нашей карточной игры к получению набора карт детьми данной пары родителей. Начнем с первой пары, несущей гены курчавых и прямых волос. Имеются четыре возможности, но лишь одна из них дает ребенка с двумя генами прямых волос, что необходимо для того, чтобы ребенок фенотипически имел прямые волосы. Любой ребенок от этого брака обладает в три раза большим числом шансов получить курчавые волосы, а не прямые, или, выражаясь иначе, из всех возможных детей этой пары в три раза чаще будут рождаться дети с курчавыми волосами, чем с прямыми.

То же самое можно было бы сказать, исходя из первого закона Менделя применительно к скрещиванию гетерозигот (см. гл. 6, рис. 13).

Рассмотрим теперь вторую раздачу карт, из которой можно будет решить, будут ли глаза ребенка карими или голубыми. Так как в этом случае материнская пара состоит из двух одинаковых карт, возможны лишь два типа выборки и оба одинаково вероятны. В итоге ребенок от этого брака обладает одинаковыми шансами родиться с карими или голубыми глазами; другими словами, среди возможных детей этой семьи половина будет иметь голубые глаза, а половина - карие. Это опять можно было бы ожидать, исходя из первого закона Менделя в приложении к скрещиванию гомозигот с гетерозиготами (см. гл. 6, рис. 15).

Мы подошли теперь к моменту, когда можно применить второй закон Менделя - третье правило нашей игры. Согласно этому правилу, вторая раздача карт независима от первой; любой ребенок, став курчавым или с прямыми волосами при первой раздаче карт, обладает одинаковыми шансами на получение карих или голубых глаз при второй раздаче; дети с карими глазами будут составлять половину всех возможных детей с курчавыми волосами, а также половину всех возможных детей с прямыми волосами. Вот несколько арифметических подсчетов вероятности приобрести следующие признаки:

карие глаза и курчавые волосы ¹/₂ от ³/₄=³/₈

голубые глаза и курчавые волосы ¹/₂ от ³/₄=³/₈

карие глаза и прямые волосы ¹/₂ от ¹/₄=¹/₈

голубые глаза и прямые волосы ¹/₂ от ¹/₄=¹/₈

Наконец, надо будет получить половые хромосомы, и эта выборка будет опять независима от двух предыдущих. Любой ребенок в этих четырех группах обладает равными шансами быть мальчиком либо девочкой, и в целом шансы родиться, скажем, мальчиком с карими глазами и прямыми волосами равны ¹/₂ от ¹/₈=¹/₁₆, тогда как шансы родиться девочкой с карими глазами и курчавыми волосами равны ¹/₂ от ³/₈=³/₁₆.

Рассмотрим теперь вопрос с точки зрения племенного животноводства. В руках селекционеров имеется порода гак называемых голубовато-желтовато-коричневых кроликов. Задача состоит в улучшении меха этого отродья путем введения ангорского гена, дающего длинную шерсть. С этой целью хозяйство приобретает ангорского самца с обычной окраской и спаривает его с крольчихами голубовато-желтовато-коричневой окраски. Их потомки получают окраску, похожую на окраску диких кроликов. Селекционер, знакомый хотя бы немного с генетикой, разочарован не будет. Он понимает, что имеет дело с рецессивными генами, присутствующими в скрытом виде в этих животных, эти гены разделятся в следующем поколении. Поэтому он скрестит кроссбридных самцов с их сестрами в надежде, что в следующем поколении обнаружится по крайней мере одна самка и один самец желаемого ангорского типа с голубовато-желтовато-коричневой окраской, которых можно в дальнейшем использовать в качестве исходного материала для нового отродья.

К сожалению, селекционер знал генетику не очень хорошо, поэтому он поставил перед собой задачу, которая, по всей видимости, принесет ему разочарование. Разберем его схему, ознакомившись с трудами по генетике кроликов. В них мы узнаем, что ангорская шерсть определяется рецессивным геном l. Таким образом, ангорский кролик-самец несет гены ll. Далее мы узнаем, что голубовато-желтовато-коричневый цвет фенотипа зависит от взаимодействия трех рецессивных генов. Один из этих генов а снимает желтое колечко на каждом волоске, которое придает шкурке дикого типа типичный пятнистый вид; гомозиготы только по этому гену несут одноцветную черную окраску. Второй ген b превращает черный пигмент в шкурке в коричневый, так что животные, гомозиготные по обоим генам и a, несут одноцветную коричневую окраску. Третий ген e ослабляет эту окраску до голубовато-желтовато-коричневого цвета. Желтовато-коричневая линия кроликов гомозиготна по всем трем генам. Далее из книг по генетике кроликов мы узнаем, что все четыре гена l, a, b и e находятся в разных хромосомах, так что их можно скомбинировать в наследственности, следуя второму закону Менделя. Теперь мы по крайней мере располагаем всем необходимым, чтобы оценить схему заводчика кроликов.

Исходное скрещивание заводчик-селекционер осуществляет между ангорским самцом, генотип ll, и голубыми желтовато-коричневыми самками, генотипически aa, bb и ее. Ни в одном отродье не представлены гены, по которым гомозиготны другие. В итоге потомство будет гетерозиготно по всем четырем генам: a+; b+; e+; l+. Эти гетерозиготы скрещивают друг с другом: (a+; b+; e+; l+)×(a+; b+; e+; l+). Заводчик заинтересован в получении генотипа aa; bb; ee; ll. Каковы шансы, что заводчик получит этот генотип среди потомства в результате своих скрещиваний?

Как в предшествующем примере, пересмотрим гены один за другим. По первому закону Менделя шансы любого потомка получить один ген a от отца и второй ген b от матери равны ¹/₄. Это же справедливо для трех других генов. Таким образом, шансы для животного приобрести гены таковы:

Так как гены лежат в различных парах хромосом, их сочетания выявляются по второму закону Менделя, и шансы получить животных aa; bb; ee; ll таковы: ¹/₄ от ¹/₄ от ¹/₄ от ¹/₄=1:256. Шансы одного из этих животных оказаться либо самцом, либо самкой равны еще половине, т. е. 1:512, и так как схема разведения предусматривает получение обоих производителей в потомстве первого из перекрестных спариваний, надо вывести 600 или больше крольчат для достижения поставленной цели. К счастью, можно, конечно, уже в первом помете обнаружить ангорского крольчонка с голубовато-желтовато-коричневой шкуркой; однако нужно быть очень счастливым, чтобы получить и самца, и самку с нужными качествами шкурки в крольчатнике с небольшим поголовьем.

При более основательном знании генетики план должен быть иной. Селекционер должен в потомстве выбирать любые комбинации, идущие в желательном направлении, и либо скрещивать их друг с другом, либо с одной из исходных линий. Так, например, если бы попался ангорский кролик черной окраски (генотип aa, возможно, гетерозиготен по b или e или по обоим вместе), можно было бы скрестить с голубовато-желтовато-коричневым отродьем согласно следующей схеме: aa; (b+?); (e+?); ll×aa; bb; ee. Все потомки этого скрещивания будут черными (aa) и гетерозиготными по l, b и e; они могут быть даже гомозиготными по b и l. Задача таким путем сократилась: комбинировать надо три или два гена вместо четырех. Если бы вместо черных ангорских в потомстве перекрестного спаривания появились бы другие комбинации генов, надо было бы предложить какую-либо иную программу разведения.

Мы остановились обстоятельно на этих двух примерах, чтобы показать, как второй закон Менделя позволяет предвидеть вероятность появления в следующих поколениях комбинаций отцовских и материнских генов. Подобные расчеты иллюстрируют лучше, чем известные соотношения, принятые в учебниках, например 9:3:3:1 или 27:9:9:9:3:3:3:1, выражающие проявления принципа свободной рекомбинации.

Наконец, обратим внимание на задачи прикладной селекции, решение которых невозможно на основе второго закона Менделя. Задача заключается в комбинировании в одной линии норок двух генов, обнаруженных по отдельности в различных линиях: доминантного гена окраски черного дерева (E) и рецессивного гена для кареглазой пастельной норки (b). Эти гены располагаются в одной и той же хромосомной паре, и при скрещивании животных этих двух линий потомки несут по одному гену на каждой хромосоме-партнере этой пары хромосом:

Когда у этих животных образуются гаметы, обе хромосомы с находящимися на них генами E и b расходятся в различные клетки. Свободное комбинирование этих генов неосуществимо. По всей видимости, единственный путь для получения линии с обоими генами - это ждать, пока в пастельной линии с карими глазами появится мутация окраски черного дерева или в линии с окраской черного дерева и мутация пастель с карими глазами. Для этого требуется не только много поколений норок, но и много поколений селекционеров норок. На практике же при скрещивании гетерозигот по генам E и b были получены щенки норок линии паломино, т. е. черные пастель с карими глазами. Как это произошло, будет описано в следующей главе.