Приложение 2

Анализ сегрегации распространенных признаков: отсутствие смещений вследствие регистрации, доминирование [876; 877]

Если тип наследования кодоминантный, так что каждый генотип соответствует своему, отличному от других фенотипу, и если анализируемые семьи выбирались из популяции независимо от генотипов их членов, то анализ сегрегационных отношений проводится непосредственно. В этом случае число индивидов в каждом генотипическом классе следует сравнивать с числом, ожидаемым из распределения на основе менделевского закона, с помощью критерия хи-квадрат, как показано в разд. 3.3.3 и табл. 3.7.

При доминировании сегрегационный анализ сложнее, чем при кодоминантном наследовании. В фенотипическом браке А¯ × а¯ содержатся два генотипических брака АА × аа и Аа × аа. Фенотипический брак А¯ × А¯ охватывает типы АА × АА, АА × Аа и Аа × Аа. Оригинальный метод сегрегационного анализа был разработан Смитом [876].

Тип брака А¯ × а¯. В этой группе представлены два генотипических брака АА × аа и Аа × аа. Первый дает только детей с генотипом Аа и с фенотипом А¯, а второй - детей Аа и аа в соотношении 1:1. Для иллюстрации используются данные по группам крови (табл. П.2.1, П.2.2). Ниже приводятся численности семей по крайней мере с одним рецессивным ребенком (аналог регистрации семей по "пораженным" потомкам)

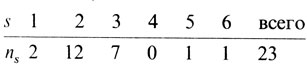
Ожидается, что в этих семьях число детей с рецессивным фенотипом подчиняется "усеченному биномиальному распределению". Например, ожидаемое соотношение двухдетных семей с 0, 1 или 2 рецессивными детьми должно быть равным 1:2:1. Однако класс с нулем рецессивов отсутствует в силу способа регистрации. Следовательно, с вероятностью 2/3 двухдетная семья будет иметь одного рецессивного потомка и с вероятностью 1/3 - двух. Ожидаемое число рецессивных детей в двухдетных семьях равно

а дисперсия

В принципе те же рассуждения можно использовать для семей с 3, 4 и большим числом детей и вычислить а₃, a₄ ... и b₃, b₄ ....

В общем случае вероятность того, что семья из s детей по крайней мере с одним рецессивным ребенком имеет точно r рецессивных детей, равна

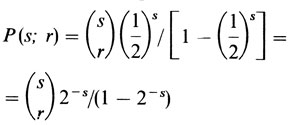
(ср. с биномиальным распределением, разд. 3.3.2). Отсюда вытекает, что

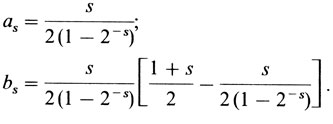
Ожидаемое общее число детей с рецессивным фенотипом в выборке составит

(используя данные Смита, приведенные здесь в табл. П.2.3). Дисперсию этой величины можно вычислить из аналогичной линейной комбинации значений b

Общий вид формул следующий:

Таблица П.2.1. Фенотипический брак А¯ × а¯

Наблюдаемое число рецессивов (из табл. П.2.1) равно

Соответствие можно проверить сравнением разности О - Е₁ = 1,377 с ее стандартной ошибкой s₁ = √V₁ = 2,925. Поскольку χ² = (O₁ - E₁)²/V₁ = 0,222, то имеется превосходное согласие.

Этот метод можно применить к фенотипическому браку А¯ × А¯ (табл. П.2.2) с той лишь разницей, что в браке Аа × Аа дети с фенотипами А¯ и а¯ ожидаются в соотношении 3:1. Ожидаемые средние значения As и дисперсии Bs можно взять из табл. П.2.3. В 10 семьях по крайней мере с одним ребенком наблюдались 11 таких детей. Сравнивая эту величину с ожидаемым средним значением Е₂ = 12,3 и дисперсией V₂ = 2,069, получаем

Таблица П.2.2. Фенотипический брак А¯ × А¯

Таблица П.2.3. Ожидаемые средние значения а_s, дисперсии b_s и величины d_s для фенотипического брака А¯ × а¯. Ожидаемые средние значения A_s, дисперсии B_s и величины D_s для фенотипического брака А¯ × А¯ [876]

Снова наблюдаемые значения превосходно соответствуют ожидаемым.

До сих пор мы не использовали генные частоты. Наблюдаемые численности семей по крайней мере с одним рецессивным ребенком нужно сравнить с ожидаемыми численностями таких семей, рассчитанными из общего количества семей в выборке. Для этого необходимы надежные оценки генных частот. Их можно получить, имея большую выборку случайных индивидов из популяции. Фенотипический брак А¯ × а¯, например, может включать два генотипических АА × аа и Аа × аа. Их ожидаемая частота 2 × р² × q² + 2 × 2pq × q² = 2p²q² + 4pq³. В то же время это значение является вероятностью того, что случайно выбранный брак будет иметь фенотип А¯ × а¯. На самом деле семья может иметь рецессивного ребенка, только если генотипический брак будет Аа × аа. Даже в этом случае вероятность иметь по крайней мере одного рецессивного ребенка среди s детей равна 1 - (1/2)^s, т. к. с вероятностью (1/2)^s будут появляться только доминантные дети.

По этой причине вероятность π того, что семья типа А¯ × а¯ с s детьми будет иметь по крайней мере одного рецессивного ребенка, составит

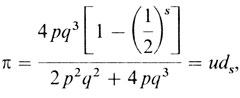
где

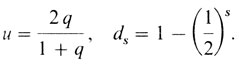
Значения d_s приведены в табл. П.2.3, и когда известны генные частоты, то легко вычислить uds. Если имеется ns семей размера s (s = 1, 2, ...), то ожидаемые среднее значение и дисперсия числа семей по крайней мере с одним рецессивным ребенком составят

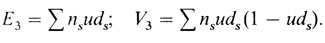
Например, генная частота q рецессивного аллеля р в системе Р равна 0,51. Следовательно, и = 0,675. Дальнейшие вычисления приведены в табл. П.2.4.

Таблица П.2.4. Ожидаемые и наблюдаемые частоты семей с рецессивными детьми, фенотипический брак А¯ × а¯

В принципе те же расчеты можно выполнить для А¯ × А¯ семей с u² и D_s = 1 - (3/4)^s вместо u и d соответственно; значения D_s приведены в табл. П.2.5.

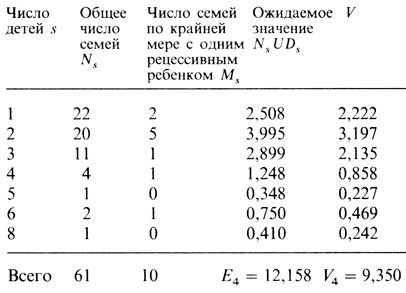
Таблица П.2.5. Ожидаемые и наблюдаемые частоты семей с рецессивными детьми, фенотипический брак А¯ × А¯

Все сравнения собраны вместе в табл. П.2.6, где приведена также сумма всех сравнений. В первых двух строках таблицы представлены значения критерия хи-квадрат для сравнения с ожидаемыми сегрегационными отношениями, а в следующих двух - наблюдаемые частоты разных типов брака сравниваются с ожидаемыми на основе закона Харди - Вайнберга, при этом используются генные частоты. Такое четкое разделение делает метод более понятным.

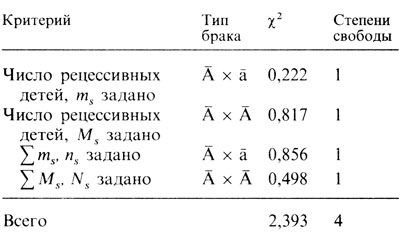
Таблица П.2.6. χ²-сравнения