
Приложение 3
Формулы и таблицы для коррекции регистрационных смещений, а также для тестирования и оценки сегрегационных отношений. Другие статистические проблемы и вычислительный пример
В приложении 2 описан метод тестирования сегрегационных отношений широко распространенных признаков (например, полиморфных вариантов). Приложение 3 содержит методы сегрегационного анализа редких признаков (в частности, моногенных заболеваний), включая коррекцию смещений, возникающих вследствие особенностей регистрации семей. Как объяснялось в разд. 3.3, сегрегационный анализ можно проводить двумя разными способами: путем тестирования эмпирических данных на соответствие заданному теоретическому сегрегационному отношению и с помощью оценки сегрегационных отношений.
В обоих случаях необходима коррекция смещений, обусловленных способом сбора данных. Следует различать два типа регистрации семей: единичный отбор (k = 0) и полный или усеченный отбор (k = 1). При единичном отборе (k = 0) каждая семья регистрируется через единственного пробанда. Примерами могут служить семейные исследования, основанные на больных в стационарах. При полном или усеченном отборе (k = 1) регистрируются все гюраженные индивиды в популяции. Коррекция сегрегационных отношений необходима потому, что в выборку не попадут сибства, в которых нет пораженных детей, хотя при гетерозиготности одного (в случае доминантного или Х-сцепленного рецессивного признака) или обоих (в случае рецессивного признака) родителей это принципиально возможно.
Ниже описываются методы тестирования соответствия теоретически ожидаемых и наблюдаемых сегрегационных отношений, а также методы оценки сегрегационных отношений. В основном мы следуем Кэлину (1955) [729]. Рекомендуемый здесь метод подразумевает использование калькулятора, предпочтительно программируемого, в противном случае следует иметь таблицы Кэлина. Сначала будут описаны методы сегрегационного анализа. Затем мы обсудим некоторые проблемы, возникающие вследствие генетической гетерогенности и примеси спорадических случаев. Кроме того, мы рассмотрим, как изучаются эффекты порядка рождения, и продемонстрируем соответствующие методы на примере опубликованного популяционного исследования глухонемоты в Северной Ирландии. Наконец, мы проанализируем некоторые более сложные проблемы регистрации, возникающие в связи с миграцией семей, а также в случаях, когда семьи охватывают более одного сибства.
На первый взгляд рекомендация следовать принципу "сделай сам", игнорируя существующие методы сегрегационного анализа, многие из которых уже реализованы в виде компьютерных программ (например, программа Мортона SEGRAN), может показаться старомодной. Однако исследователь, который берет на себя труд самостоятельно пройти все этапы такого анализа, будет вознагражден способностью критически оценить получаемые результаты с учетом особенностей и возможных изъянов своих данных. Те читатели, которые имеют доступ к персональному компьютеру (PC) и знакомы с алгоритмическим языком BASIC., могут легко написать программу в соответствии с описываемыми ниже методами.
Тестирование эмпирических семейных данных на соответствие заданному сегрегационному отношению. В этом подходе наблюдаемые численности r пораженных в сибствах размера s сравниваются с их ожидаемыми значениями Es(r). Ожидаемые значения вычисляют по формулам sp/(1 - qs) (для полного или усеченного отбора, k = 1) и (s - 1) р + 1 (для единичного отбора, к = 0) с помощью нескольких программных операций карманного калькулятора. Здесь s - количество детей в сибстве, ns - число сибств размера s, r - число пораженных сибсов, р - тестируемое сегрегационное отношение, q = 1 - p. Чтобы вычислить ожидаемое значение ∑ Es(r) для всего набора имеющихся сибств, нужно просуммировать соответствующие ожидаемые значения Es(r). Например, если семейные данные содержат 5 сибств размера 6 с двумя пораженными сибсами и одно сибство размера 8 с тремя пораженными сибсами, если каждое из этих сибств имеет одного пробанда (единичный отбор, k = 0) и если ожидаемое сегрегационное отношение равно 0,25 (рецессивное наследование), то ожидаемая численность пораженных для всего набора сибств получается следующим образом:
∑ = 5 × 2,25 + 1 × 2,75 = 14,00.
Наблюдаемое число пораженных сибсов равно 5 × 2 + 1 × 3 = 13. Теперь эти два значения можно сравнить друг с другом, используя формулу χ = (О - E)/V, дисперсия вычисляется по формуле
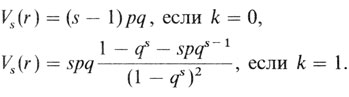
Дисперсия одного сибства составит
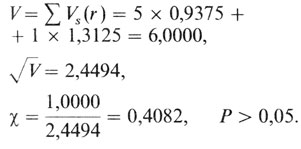
В табл. П.3.1 представлен пример вычислений, связанных с генетическим анализом глухонемоты.
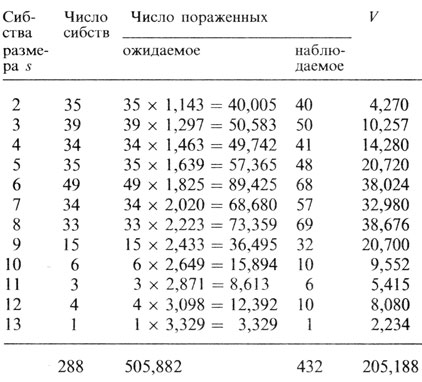
Таблица П.3.1. Тестирование сегрегационного отношения для глухонемоты в соответствии с априорным методом: предполагается, что брак между фенотипически непораженными генотипически представляет собой брак гетерозигот Аа × Аа
Оценка сегрегационного отношения в семейных данных. Описанный выше метод тестирования отвечает лишь на вопрос, согласуется ли имеющийся набор эмпирических численностей с их значениями, ожидаемыми на основе конкретной генетической гипотезы. Однако чаще такая гипотеза неочевидна. Следовательно, целесообразнее оценивать сегрегационное отношение. Первыми такими методами были вайнберговские "Geschwistermethode" (сибсовый метод) и "Probandenmethode" (пробандовый метод). Сибсовый метод применяется тогда, когда все пораженные сибсы являются одновременно и пробандами, т. е. когда k = 1. В этом случае для каждого пораженного сибса подсчитывают число его непораженных и пораженных сибсов. Например, сибство может содержать 6 членов, из которых трое поражены, а трое здоровы. Сибсовый метод дает следующий результат: пораженных будет 3×2 = 6 сибсов, а непораженных - 3×3 = 9 сибсов (у каждого из трех пораженных имеем по два пораженных и три непораженных сибса). Оцениваемое сегрегационное отношение равно
pˆ = 3×2 / 3×2+3×3 = 6/15 = 0,4.
Если не все пораженные сибсы зарегистрированы в качестве пробандов, то упомянутая выше процедура преобразуется так, чтобы подсчет вести только для пробандов. Преобразованная процедура получила название пробандового метода. Если каждое
сибство было зарегистрировано через одного пробанда, то подсчет осуществляется только один раз. Для упомянутого выше сибства это означает рˆ = 2/5 = 0,4 (случай к - 0). Для одного-единственного сибства две оценки для k = 1 и k = 0 идентичны. Однако они могут различаться, если выборка содержит много сибств разного размера. В этом случае оценка для k = 1 дает наибольшее значение р, а для к = 0 - наименьшее. Позже были разработаны более сложные методы оценки. Один из них предложил Финни [663]. Мы опишем его в версии Кэлина [729]. Для каждого сибства вычисляется взвешенный шанс
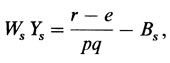
здесь s - число всех сибсов, а r - число пораженных сибсов соответственно, и
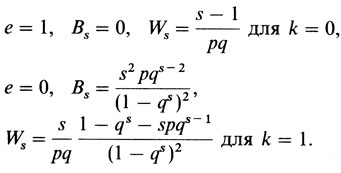
Взвешенные шансы WsYs и сами веса Ws суммируются по отдельности для всех сибсов. То значение р, для которого частное суммы шансов и суммы весов
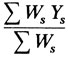
равно р, и есть оценка рˆ истинного сегрегационного отношения. Кроме случаев единичного отбора (k = 0), значение рˆ можно вычислить лишь итеративно. Начинают с первого приближения р1 оценки рˆ, в качестве которого можно принять оценку, получаемую по пробандовому методу Вайнберга (см. выше), затем, используя р1, вычисляют новое приближение р2 = ∑WsYs/∑W и заменяют р1 на р2. Эта процедура повторяется до тех пор, пока р2 не становится практически равным р1. Описанное вычисление можно упростить следующим образом. Если р2 больше р1 (это означает, что р1 < рˆ), то вычисление повторяется с большими значениями р1, пока р2 не станет меньше, чем p1. Наоборот, если р2 исходно меньше, чем р1 (это означает, что р1 > рˆ),
то р1 уменьшается до тех пор, пока р2 не станет больше, чем р1. Если в процессе вычисления p оказывается между р1 и р2, то оно вычисляется с помощью линейной интерполяции. Значение рˆ можно представить как результат пересечения двух прямых линий
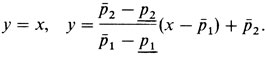
Правые части этих двух уравнений приравниваются, и полученное уравнение решается относительно х, что дает pˆ. Дисперсию вычисляют следующим образом:
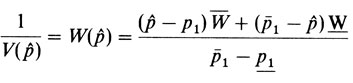
(линейная интерполяция между весами W- и W¯, соответствующими р1- и р1¯). Эта процедура будет продемонстрирована ниже на практическом примере. Для k = 0 окончательная оценка рˆ равна
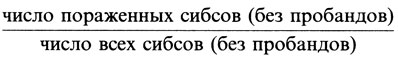
(пробандовый метод Вайнберга) и достигается уже на первом шаге итераций.
Давайте снова рассмотрим наш пример: сибство с s = 6 детьми, из которых r = 3 поражены. При полном отборе (k = 1) следующий шанс вычисляется, начиная с предварительной оценки p1 = 0,45,
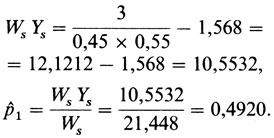
Здесь численные значения Bs и Ws вычисляются в соответствии с уравнениями П.3.1. Поскольку вычисленное значение р1ˆ выше первоначального значения 0,45, то вычисление повторяется с р2 = 0,5:
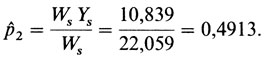
Истинное значение рˆ находится между этими двумя оценками, оно может быть найдено с помощью интерполяции.
До сих пор мы рассматривали только два предельных случая k = 1 (полный отбор) и k = 0 (единичный отбор). Однако существуют методы и для неполного множественного отбора, т. е. для любого числа пробандов в сибстве. Мортон и др. [800; 802; 954; 963] усовершенствовали этот метод, приняв в расчет количество регистрации, приходящихся на одного пробанда. В ходе популяционного исследования пробанды могут быть зарегистрированы не один раз, а несколько. Теоретически такая множественная регистрация действительно позволяет оценивать реальную частоту признака в популяции, когда регистрация неполная. Предположим для простоты, что регистрация проходит в два этапа, что вероятность регистрации на каждом этапе равна π и шансы быть зарегистрированным для любого индивида на первом и втором этапах независимы друг от друга. Тогда вероятность быть зарегистрированным дважды равна π2, а вероятность быть зарегистрированным один раз (либо на первом этапе, либо на втором) равна 2π × (1 - π). Отношение
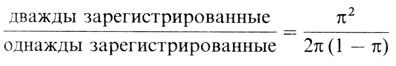
позволяет вычислить π.
Однако это вычисление подразумевает выполнение очень существенного условия. Разные регистрации пробанда должны быть независимыми друг от друга. В разд. 3.3.4 объяснялось, что даже единичные регистрации разных пробандов в одной семье почти никогда не являются независимыми. Из всех медицинских и эпидемиологических исследований ясно, что, какие бы практические пути ни были выбраны для сбора семейного материала, регистрации пробандов никогда не будут независимыми. Возьмите два крайних примера: врач, страдающий наследственной болезнью, легко будет зарегистрирован несколько раз в разных больницах, где он консультирует, поскольку они специализируются на его болезни, тогда как сезонный сельскохозяйственный рабочий, весьма вероятно, не будет зарегистрирован ни разу при любом способе обследования.
По нашему мнению, эти усовершенствованные методы анализа неадекватны для большинства семейных исследований. Мы думаем также, что методы, учитывающие множественный или пробандовый отбор, не должны использоваться, потому что регистрация пробандов внутри одной и той же семьи не является независимой (см. разд. 3.3.4). Более того, мы считаем опасным применять эти методы к выборкам семей, для которых строго не обоснована независимая регистрация. В свете всех предложенных усовершенствований статистического анализа нам кажется корректной следующая рекомендация Кэлина [729] и Смита [878].
На практике генетик, исследующий редкий признак, находится в затруднительном положении. Он может лишь высказывать определенные утверждения о сегрегационных отношениях, только если он точно знает, каковы статистические свойства его метода сбора данных. Однако если признак редкий, то исследователь будет стремиться собрать столько случаев, о скольких он сможет узнать по обращениям в больницы, к семейным врачам и т. д., но со статистической точки зрения это не даст хорошо определенной выборочной схемы. Практически неизбежно в таких случаях возникнут некоторые сомнения относительно точного значения р. Обычно предполагают, что ситуация будет промежуточной между усеченным и единичным отбором, так что простейший метод тестирования, по-видимому, должен показать, что число пораженных не больше, чем можно было ожидать при гипотезе полного отбора, и не меньше, чем можно было ожидать при гипотезе единичного отбора [878].
По нашему мнению, единственным исключением из этого правила является полная регистрация всех семей с пробандами в одной популяции при полном или усеченном отборе, когда семьи регистрируются через поколение родителей. Следовательно, эпидемиологические исследования редких наследственных болезней должны основываться, когда это возможно, на полной регистрации всех случаев в определенной популяции и для заданного периода времени.
Не следует переоценивать статистические методы коррекции плохих исходных данных. Даже превосходный повар не способен приготовить отменного жареного зайца из дохлой кошки. (Между прочим, один большой секрет французской кухни заключается в настойчивом требовании использовать только очень хорошие ингредиенты.)
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'