Проблемы, связанные с тестированием статистических гипотез

Генетическая гетерогенность. Описанные выше методы дают удовлетворительные результаты, когда изучаемый признак генетически гомогенен и тип наследования простой. При этих условиях метод тестирования обнаруживает согласие между ожидаемыми и наблюдаемыми значениями и дает оценку рˆ, близкую к ожидаемому сегрегационному отношению (25% в случае рецессивного наследования). Но даже в этом случае остается открытым вопрос о количестве вовлеченных генов с одинаковым типом наследования, т. е. вопрос о том, существует ли генетическая гетерогенность. Чтобы ответить на него, надо обследовать детей от брака двух гетерозигот. Если все их дети поражены, можно сделать вывод об участии одного и того же локуса.

При рецессивном наследовании о генетической гетерогенности можно судить, исходя из относительных частот близкородственных браков (особенно браков двоюродных братьев и сестер) среди родителей пробандов и в общей популяции (разд. 3.6.1). Это отношение возрастает с уменьшением частоты гена. Следовательно, если уровень родства намного выше, чем ожидается на основе генной частоты, вычисленной из наблюдаемой частоты признака в предположении одного рецессивного гена, то можно заключить, что существует более одного рецессивного гена. Частоты отдельных генов будут ниже, чем их суммарная частота, что и объясняет более высокий уровень родства.

Хотя теоретически такой аргумент убедителен, на практике его следует использовать очень осторожно, поскольку он предполагает случайное распределение близкородственных браков в популяции. Но семьи с рецессивными болезнями часто будут попадать в выборку из полуизолятов, в которых доля близкородственных браков обычно выше, чем в общей популяции. Следовательно, этим аргументом можно пользоваться только вместе с другими фактами.

Примесь спорадических случаев. Другая проблема возникает, когда реальное сегрегационное отношение оказывается ниже, чем ожидаемое. Здесь наиболее очевидное объяснение - примесь спорадических случаев (ненаследственных вариантов или новых доминантных мутаций). Тогда количество сибств только с одним пораженным должно быть выше его ожидаемого значения (Е), которое в соответствии с биномиальным распределением равно

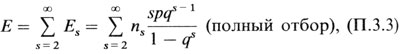
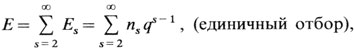
где n_s - число сибств размера s. Это ожидаемое значение можно вычислить, если подставить вместо р оценку рˆ, а затем сравнить его с ожидаемой частотой О, подсчитав

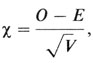
который распределен приблизительно нормально,

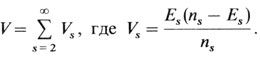
Пример приводится в конце данного приложения.

Эта проблема не имеет практического значения в условиях полного доминирования: случай классифицируется как спорадический (ненаследственный или новая мутация), если оба родителя здоровы. Иная ситуация имеет место при неполной пенетрантности. Здесь этот метод может помочь провести различие между случаями, в которых ген присутствовал у одного из родителей, но не проявился, и реальными спорадическими случаями с генотипически нормальными родителями, т. е. новыми мутациями. Это особенно важно, когда у нас есть основания предполагать рецессивное наследование, а оценка рˆ меньше 0,25. В такой ситуации, когда анализ показывает, что число сибств только с одним пораженным возросло, нам может понадобиться оценка истинного сегрегационного отношения. Существуют два способа получения таких оценок. Во-первых, анализ может быть ограничен сибствами по крайней мере с двумя пораженными. Во-вторых, сибствами, в которых родители состоят в родстве, поскольку большинство из этих больных будут рецессивными гомозиготами. Можно оценить число спорадических случаев, снова используя биномиальное распределение (пример приведен ниже).

Порядок рождения и возраст матери. Гипотеза простого типа наследования предсказывает также, что последовательность пораженных и непораженных сибсов случайна и что нет влияния порядка рождения или возраста отца или матери. Наиболее общие критерии случайности последовательностей базируются на теории случайных процессов и адаптированы к использованию в анализе родословных человека. Старое утверждение, что при анемии Фанкони сибсы, пораженные рецессивной болезнью крови (разд. 5.1.6) образуют кластеры внутри сибств, недавно было опровергнуто тестом, основанным на теории случайных процессов [895].

Примеры эффектов возраста отца и матери приведены в гл. 5. Весьма полезным подходом следует считать исследование порядка рождения. Очевидно, что порядок рождения коррелирует с возрастом отца или матери и может исследоваться сам по себе по семейным данным без обращения к контрольной популяции. Был табулирован полезный критерий [698]. Пусть А - сумма порядков рождения пораженных сибсов, s - число всех сибсов и r - число пораженных сибсов в сибстве. Тогда математическое ожидание и дисперсия величины 6А (которую проще табулировать, чем А), когда можно классифицировать всех сибсов, равны

При неполной классификации (см. оригинал) формулы сложнее. Математические ожидания и дисперсии приведены в табл. П.3.2.

Таблица П.3.2. Вычисление эффектов порядка рождения. Среднее значение (жирный шрифт) и дисперсия величины 6А в полном сибстве [698]