XV. Вычисление менделевских отношений

Если вы вернетесь к главе XIII и вспомните об удвоении числа типов гамет с каждой парой генов (если данный организм по ним гетерозиготен), то легко убедитесь в том, что методом решетки можно пользоваться только при скрещиваниях, в которых рассматривается очень небольшое число пар генов. При скрещиваниях с тремя парами генов организмы F₁ образуют 8 типов гамет (2 × 2 × 2), и решетка, характеризующая F₂, имеет 64 квадрата (8 × 8). При скрещиваниях с четырьмя парами генов организмы F₁ образуют 16 типов гамет (2 × 2 × 2 × 2), и решетка состоит из 256 квадратов (16 × 16).

Теперь выведем отношение 9:3:3:1 более простым способом, имеющим то преимущество, что им можно пользоваться при рассмотрении любого числа пар генов. Воспользуемся примером, который иллюстрирует рис. 34. Вместо выяснения, какие гаметы образуются у растений F₁, определим, каким будет потомство (F₂) в результате самооплодотворения растений F₁. В соответствии со вторым законом Менделя расщепление по разным признакам происходит независимо, поэтому можно рассматривать каждое расщепление последовательно одно за другим и затем комбинировать полученные результаты:

1. Окраска цветка Rr × Rr дает 3/4 растений с краевыми цветками и 1/4 растений с белыми.

2. Форма боба Рр × Рр дает 3/4 растений с гладкими бобами и 1/4 растений с ребристыми бобами.

Теперь мы подошли к решающему моменту. Поскольку расщепление по форме боба не зависит от расщепления по окраске цветка, то 3/4 растений с гладкими бобами и 1/4 растений с ребристыми бобами будут как среди красноцветковых, так и среди белоцветковых растений.

Поэтому доля красноцветковых растений с гладкими бобами составит 3/4 от 3/4, т. е.

красноцветковых растений с ребристыми бобами

белоцветковых растений с гладкими бобами

белоцветковых растений с ребристыми бобами

Освободившись от общего знаменателя, равного 16, получим отношение 9:3:3:1.

Самым простым способом получения такого отношения является перемножение членов, характеризующих результаты двух независимых расщеплений, например: (3/4 красных + 1/4 белых) × (3/4 гладких + 1/4 ребристых) = 9/16 красных гладких + 3/16 красных ребристых + 3/16 белых гладких + 1/16 белых ребристых.

Общий знаменатель опять можно опустить.

Обычно для обозначения доминантных или рецессивных признаков используют буквы соответствующих доминантных или рецессивных генов:

Такие сокращения вполне допустимы, если помнить, что в данном случае эти буквы соответствуют признакам, а не генам; если бы они обозначали гены, то они были бы записаны парами. В книгах эти буквы обычно выделяют другим шрифтом; в своих записях вы могли бы использовать чернила другого цвета.

На рис. 36 изображены особи крупного рогатого скота F₂, полученные в результате скрещивания особей (Р₁), отличающихся друг от друга тремя парами несцепленных генов:

В - ген черной окраски, b - ген рыжей окраски (черная окраска доминирует);

Р - ген комолости, р - ген, определяющий наличие рогов (комолость доминирует);

F - ген, определяющий белую голову (как у херфордского скота);

f - ген, определяющий окрашенную голову (белая окраска доминирует).

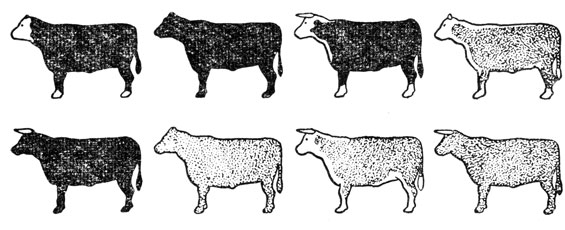
Рис. 36. Расцепление по трем несцепленным парам генов при скрещивании между быком абердин-ангусской породы и коровой херфордской породы

Проводится скрещивание между черным комолым быком абердин-ангусской породы и рыжей рогатой херфордской коровой с белой головой

F₁ (скрещенные друг с другом) Bb Pp Ff × Bb Pp Ff. Чтобы получить отношение фенотипов в F₂, перемножим (3В + 1b) × (3Р + 1р) × (3F + 1f). При этом получим следующий результат:

3B × 3Р × 3F = 27 черных комолых животных с белой головой; 
3В × 3Р × 1f =  9 черных комолых животных с окрашенной головой; 
3В × 1р × 3F =  9 черных рогатых животных с белой головой; 
1b × 3Р × 3F =  9 рыжих комолых животных с белой головой; 
3В × 1р × 1f =  3 черных рогатых животных с окрашенной головой; 
1b × 3Р × 1f =  3 рыжих комолых животных с окрашенной головой; 
1b × 1р × 3F =  3 рыжих рогатых животных с белой головой; 
1b × 1р × 1f =  1 рыжее рогатое животное с окрашенной головой.

Правильность этого вычисления можно проверить разными способами. Прежде всего сумма всех животных равна 64, и это согласуется с тем, что решетка в данном случае состояла бы из 64 квадратов. Затем каждый из трех рецессивных признаков (рыжий цвет, наличие рогов и обычная окраска головы) проявляется у 16 животных, т. е. у 1/4 всех особей. И, наконец, каждое из восьми (2×2×2) различных сочетаний трех пар признаков можно найти в одной из восьми строчек данного расчета.

На практике же скотовод вряд ли заинтересовался бы отношением всех возможных фенотипов в F₂. Но ему, может быть, важно узнать вероятность появления какого-то определенного фенотипа, например черного рогатого быка с окраской головы, свойственной херфордской породе. Какова вероятность появления животного с определенными признаками? Этот вопрос можно сформулировать иначе. Какая часть животных будет иметь данный фенотип? Действительно, вероятность выпадения орла при однократном подбрасывании монеты равна 1/2, так как при большом числе подбрасываний орел выпадет в половине случаев. Вероятность появления черного рогатого животного с белой головой в F₂ (от скрещивания животных абердин-ангусской и херфордской пород) составляет 9/64, поскольку при очень большом числе особей F₂ животные этого типа составят 9/64 их общего числа. Вероятность того, что таким животным окажется бык, составляет 1/2 от 9/64, т. е. 9/128.

Для ответа на подобный вопрос совсем не обязательно рассматривать все потомство. Вместо этого можно поступить следующим образом.

Скотовод хочет получить черного рогатого быка с белой головой. Он ожидает появления такого быка в потомстве от скрещивания Bb Pp Ff × Bb Pp Ff.

При этом скрещивании вероятность появления в потомстве черного животного составляет 3/4 (рассматривается только Bb × Bb); рогатого животного - 1/4 (рассматривается только Рр × Рр); животного с белой головой - 3/4 (рассматривается только Ff × Ff); животного нужного пола (быка) - 1/2.

Таким образом, вероятность появления черного рогатого быка с белой головой равна 9/128 (т. е. 3/4 × 1/4 × 3/4 × 1/2), что составляет около 7%.

Какова вероятность того, что бык с этим фенотипом окажется чистопородным по всем трем признакам? Поскольку наличие рогов - рецессивный признак, каждый рогатый бык гомозиготен по гену, определяющему наличие рогов, и поэтому он чистопороден по данному признаку. Но для доминантных признаков (черная окраска и белая голова) всего 1/3 быков будет гомозиготна по гену черной окраски и 1/3 - по гену, определяющему белую голову. Следовательно, только 1/3 от 1/3 животных (т. е. 1/9) будет гомозиготной по всем трем генам и, соответственно, чистопородной по всем трем признакам. Таким образом, вероятность появления чистопородного черного рогатого быка с белой головой в F₂ (от скрещивания между животными херфордской и абердин-ангусской пород) равна лишь 1/128.

Рассмотренный метод имеет большое практическое значение. Он позволяет селекционеру вычислить, сколько нужно иметь животных в потомстве, чтобы получить организм с определенным фенотипом или генотипом. Без такого расчета он может слишком поздно обнаружить, что начатую работу ему не удастся довести до конца.

Используем этот метод для решения двух вопросов, связанных с разведением мышей (см. перечень генов ранее).

1. Какова вероятность получения мыши-альбиноса с волнистой шерстью, короткими ушами и скрученным хвостом в результате следующего скрещивания:

Вероятность получения в потомстве альбиноса составит 1/4 (Сс × Сс), мыши с волнистой шерстью - 1/2 (ww × Ww), мыши с короткими ушами - 1/4 (Ss × Ss) и мыши со скрученным хвостом - 1/2 (Кк × кк), т. е. 1/4 × 1/2 × 1/4 × 1/2 = 1/64.

Если вы усвоили данный метод, то можно записать сочетание признаков, которое необходимо получить, и под каждым из признаков - вероятность его получения.

Альбинизм   Волнистая   Короткие   Скрученный 
              шерсть       уши        хвост 

   1/4    ×    1/2    ×    1/4   ×     1/2   =   1/64.

2. Самец (Rr Cc Ss Kk) скрещивается с самкой (Rr Сс ss kk). Какова вероятность получения:

а) самца с генотипом RR CC Ss Kk?

Ответ: ¹/₂ × ¹/₄ × ¹/₂ × ¹/₂ × ¹/₂ = ¹/₁₂₈;

б) самки-   с королевской   длинными   прямым 
альбиноса      шерстью        ушами    хвостом
Ответ: 1/2 × 1/4 × 3/2 ×        1/2   ×   1/2   =   3/128.

Выводы

1. Метод решетки можно применять для скрещиваний, в которых рассматривается две или три пары несцепленных генов. При более сложных скрещиваниях может быть использован способ перемножения.

2. Будучи примененным к скрещиванию Аа Вb Сс × А а Вb Сс, этот способ позволяет установить фенотипы потомства путем перемножения, например (3А + 1а) × (3В + 1b) × (3С + 1с), где буквы А, а, В, b, С, c обозначают признаки, определяемые генами А, а, В, b, С, с.

3. Выяснить вероятность получения в потомстве от данного скрещивания особи с определенным фенотипом или генотипом - значит рассчитать, какую часть составят особи данного типа при очень большом числе потомков.

4. Вероятность появления особи с данным сочетанием признаков или генов непосредственно вытекает из вероятности появления каждого признака или каждой пары генов.

Задание

Ниже приведен перечень генов человека (все гены несцепленные):

В определяет карие глаза, доминирует над геном b голубых глаз;

r определяет рыжий цвет волос, рецессивен по отношению к гену R (волосы иного цвета);

С определяет вьющиеся волосы, доминирует над геном с гладких волос;

Р вызывает многопалость, доминирует над геном р, определяющим нормальное число пальцев (на руках и ногах);

d вызывает глухоту, рецессивен по отношению к гену Z), определяющему способность слышать.

Мужчина с генотипом Bb rr Cc Pp Dd вступает в брак с женщиной, имеющей генотип bb Rr Сс pp Dd.

1. Каковы фенотипы родителей?

2. Какова вероятность рождения ребенка с генотипом bb rr сс pp dd, с генотипом Bb Rr Cc Pp DD и с генотипом Bb rr CC Pp Dd?

3. Какова вероятность рождения дочери:

а) глухой, с карими глазами, рыжими вьющимися волосами и с нормальным числом пальцев?

б) с нормальным слухом, голубыми глазами, рыжими гладкими волосами, многопалой?

в) с нормальным слухом, карими глазами, вьющимися нерыжими волосами и с нормальным числом пальцев?