
III.1.1. Логика анализа и статистическая проверка гипотез. Метод χ2
Логика анализа сводится к предложению гипотез (нулевая гипотеза - Н0) на основе известных "модельных" расщеплений и их статической проверке. Нулевая гипотеза предполагает соответствие между опытными и теоретическими рассчитанными данными. В реальных ситуациях почти всегда наблюдаются отклонения от теоретически ожидаемого расщепления. Эти отклонения могут быть прежде всего следствием вероятностного характера расщеплений и носят случайный характер. В определенных случаях их причины связаны с нарушением любого из условий менделевско-го наследования (например, с гибелью гамет или зигот определенного генотипа и т. д.). Наконец, они могут возникать из-за ошибок или неопытности экспериментатора (неумения различать фенотипы, неправильной постановки опыта, небрежности в записи результатов и др.).
Поэтому для проверки соответствия опытного и теоретически рассчитанного расщепления прежде всего необходимо оценить величину отклонения, его значимость. Чаще всего для этих целей применяют метод χ2.
Например, если при скрещивании львиного зева с красными и желтыми цветками в F1 получили растения с розовыми цветками, а в F2 произошло расщепление: 54 с красными, 122 с розовыми и 58 с желтыми цветками, то можно выдвинуть нулевую гипотезу (Но) о моногенном характере различий между исходными формами и о неполном доминировании на основании "похожести" расщепления на соотношение 1:2:1. Теоретический расчет потомков в каждом классе расщепления проводится на основе данной гипотезы. Для этого общую сумму потомков делят на величину возможных сочетаний гамет (в данном случае равную 4-1+2+1): 234/4 = 58,5 и определяют теоретически ожидаемое расщепление (q), которое записывают в таблицу вместе с опытными данными. Затем определяют величину отклонения (d), которую возводят в квадрат (d2), чтобы избавиться от отрицательных величин. Квадрат отклонения делят на теоретически ожидаемую для каждого класса величину. Сумма этих величин и представляет собой показатель χ2. После этого по таблице Фишера (приложение 1) с учетом степеней свободы определяют вероятность случайности отклонения (Р). (Под степенями свободы понимают число классов, которым можно придавать произвольные значения - Серебровский, 1970). Это число на единицу меньше числа классов в расщеплении.
Значения χ2, приведенные в таблице, указывают те границы, до которых полученные значения χ2 остаются с определенной вероятностью в рамках случайных отклонений, т. е. свидетельствуют о соответствии опытных и теоретически ожидаемых данных. Если значения χ2 превышают табличные при соответствующих степенях свободы, то это означает, что отклонение в опыте неслучайно, оно не может быть объяснено причинами статистического характера. Следовательно, нулевая гипотеза должна быть отброшена. Допустимой границей вероятности в статистике принято считать величину 0,05. Нулевая гипотеза отвергается, если значение χ2 выше того, что дано в графе р = 0,05 при соответствующем числе степеней свободы. Если значение χ2 не превышает значения χ2, находящегося в графе р = 0,05, нет оснований для отбрасывания гипотезы.
Результаты расщепления по окраске львиного зева. Проверка по χ2.
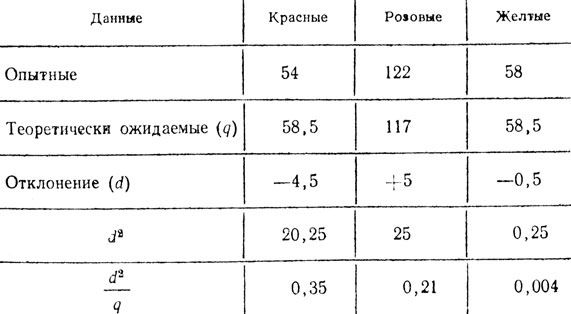
χ2 = Σd2/q = 0,35 + 0,21 + 0,004 = 0, 564
0,75<P<0,90.
Можно принять, что отклонение в опыте носит случайный характер. Нулевая гипотеза не отвергается.
Метод χ2 позволяет установить соответствие опытных и ожидаемых результатов по каждому классу и по всему расщеплению в целом. Следует помнить, что этот метод не применим к значениям, выраженным в относительных числах и процентах, а также к выборкам с числом особей в каком-либо из теоретических классов меньше пяти. Оценка отклонения по критерию χ2 ничего не говорит в пользу гипотезы, но на ее основе отвергают ложные гипотезы, если отклонение значимо, т. е. нет соответствия между опытными и теоретически рассчитанными величинами.
Обычно опыты ставят в нескольких повторностях, а в случае изучения наследования у объекта с низкой плодовитостью практически всегда приходится иметь дело с результатами нескольких опытов. Расщепления в разных опытах могут различаться как в силу случайных причин, так и за счет каких-либо нарушений биологических механизмов расщепления. В связи с этим возникают следующие вопросы.
- Как оценить возможность суммирования данных нескольких опытов?
- Как проводить оценку расщепления в малочисленных семьях?
- Каким должен быть минимальный объем выборки, необходимый для анализа расщепления?
Для оценки однородности результатов, полученных в разных опытах, также используют метод χ2. При этом вычисляют - χ2 в каждом опыте отдельно и затем суммируют эти значения. При этом число степеней свободы (df) равно сумме чисел свободы в каждом опыте; -χ2 по суммарным данным всех опытов.
Сравнивая значение вычисленных таким образом χ2, определяют, однороден ли материал в этих опытах. Поясним это на примере.
В шести опытах на горохе были получены следующие расщепления по окраске растений:

Значение χ2, определенное по суммарным данным всех опытов, равно 3,06, оно характеризует случайность отклонения в опыте от теоретически ожидаемого. χ2, определенный по сумме хи-квадратов шести опытов, равен 41,15. Разница между хи-квадратами, вычисленными по сумме χ2 шести отдельных опытов, и χ2. определенным по суммарным данным этих опытов, характеризует гетерогенность материала.
Определим, однородны ли данные приведенных выше опытов.

Можно сделать вывод, что материал в опытах неоднороден (χ2 = 38,09): в трех из них - 1,4 и 5 - наблюдается сильное отклонение от теоретически ожидаемого расщепления; соответствие ожидаемому расщеплению, определенное по суммарным данным, очевидно является случайным.
Необходимо продолжить анализ для выяснения причин отклонений в этих опытах.
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'