
§ II.3. Селекционные ограничения
Можно придумать много внешних ограничений и внутренних связей, которые сделали бы систему реакций более конкурентной (см. проблемы "борьбы" в книге В. Вольтерра [53]). Однако есть две простые процедуры, которые послужат нам общей основой для теории отбора. Обе эти процедуры можно связать с теорией Пригожина и Глансдорфа [47], которая рассматривает химические реакции вблизи стационарного состояния.
Потребуем, чтобы система находилась в стационарном состоянии. В термодинамической теории (см. гл. I) такие системы можно рассматривать либо при постоянных реакционных силах, либо при постоянных реакционных потоках.
Подобным же образом при рассмотрении информационного ящика, введенного в § II.1, мы можем поддерживать постоянной либо общую организацию (и тем самым некое суммарное сродство, см. табл. 5), либо суммарный поток единиц (который определяется потоками мономерных единиц внутрь и наружу, а также суммарными реакционными потоками внутри ящика).
Точнее, первое условие означает, что суммарное число организованных и неорганизованных единиц, а также "степень организованности" в ящике должны поддерживаться постоянными. Физически этому можно способствовать, если забуферить концентрации m1 ... mλ богатых энергией мономеров и регулировать (посредством ф0) суммарный поток таким образом, чтобы суммарное число носителей информации оставалось постоянным.
Тогда в случае постоянной общей организации налагаются следующие ограничения:
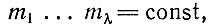 (II.24)
(II.24)
вследствие чего 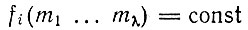 и могут быть включены в
и могут быть включены в 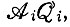
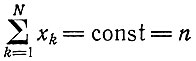 (II.25)
(II.25)
(или, если мы рассматриваем различные классы ν, 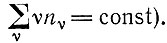
Поток разбавления ф0 нужно регулировать таким образом, чтобы он компенсировал суммарную избыточную продукцию:
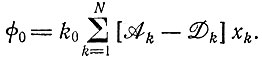 (II.26)
(II.26)Альтернативное условие отбора допускает, чтобы содержимое ящика варьировало, но тогда приток мономерных, богатых энергией единиц (ф1 ... фλ), а также реакционный поток, т. е. суммарная скорость сборки и распада носителей информации (включая и отток бедных энергией продуктов разложения), должны быть постоянными:
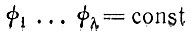 (II.27)
(II.27)или, если мономеры получаются из одного и того же источника,
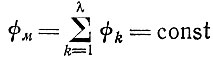
и
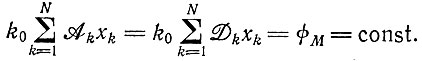 (II.28)
(II.28)Экспериментальное осуществление и теоретическое рассмотрение последнего случая более трудны. Некоторые процессы в природе могут протекать в условиях, близких к этим. В течение какого-то времени энергия может поставляться с постоянной скоростью (например, солнечная энергия), так что количество богатого энергией вещества может изменяться таким образом, чтобы скорость продукции оставалась постоянной. (Увеличение констант скоростей компенсируется уменьшением концентрации мономерных единиц.) Аналогично число носителей информации может возрасти до такого уровня, когда их распад будет регулироваться скоростью их образования. Строгое соблюдение этого условия, однако, требует сложных методов контроля. Для эволюционных экспериментов легче поддерживать условия постоянной общей организации (см. опыты С. Спигелмана с фагом Qβ, описанные в гл. VII). Можно построить "эволюционные машины", которые будут автоматически контролировать и поддерживать определенные условия; можно также представить себе другие ограничения, включающие различные комбинации из двух приведенных выше условий.
Замечание: Хотя эта детализация определенных условий важна для понимания принципов эволюции и количественной оценки экспериментальных данных, совершенно не обязательно, чтобы какой-либо реальный эволюционный процесс в природе происходил при этих специальных условиях, так же как ни одна паровая машина не работает в точности при условиях термодинамического равновесия в цикле Карно.
Вернемся теперь к феноменологическим уравнениям и перепишем их с должным учетом двух различных селекционных ограничений:
а) Постоянная общая организация
Введем определения:
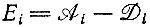
- (избыточная) продуктивность, (II.29)
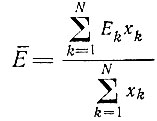
- "средняя продуктивность", (II.30)
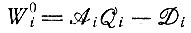
- "селективная ценность". (II.31)
Все эти величины относятся к ограничению постоянной общей организации.
Заменив φ0 согласно формулам (II.15) и (II.26), мы можем переписать уравнение (II.17) в виде
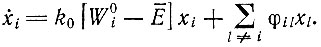 (II.32)
(II.32)
Член 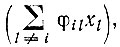 соответствующий "исправлению ошибок" или "обратному потоку информации", обычно оказывается пренебрежимо малым для любой отобранной главной копии im. Такая главная копия, однако, всегда будет сопровождаться "кометным хвостом" ошибочных копий, постоянное присутствие которых обусловлено главным образом членом φimxm (индексом m обозначена отобранная главная копия). Уравнение (II.32) существенно нелинейно - даже для постоянных значений Ai, Qi и Di - вследствие того, что каждая популяционная переменная xi входит в выражение для средней продуктивности Е¯. Таким образом, все уравнения связываются этим членом, который дает скользящее и саморегулирующееся пороговое значение, отражающее самоорганизацию системы. Будет расти численность только тех носителей информации, "селективные ценности" W0i которых находятся выше порога Е¯. Вследствие своего роста они постоянно сдвигают порог Е¯ в сторону все больших значений, пока не достигается оптимум Е¯, равный максимальной селективной ценности всех имеющихся видов:
соответствующий "исправлению ошибок" или "обратному потоку информации", обычно оказывается пренебрежимо малым для любой отобранной главной копии im. Такая главная копия, однако, всегда будет сопровождаться "кометным хвостом" ошибочных копий, постоянное присутствие которых обусловлено главным образом членом φimxm (индексом m обозначена отобранная главная копия). Уравнение (II.32) существенно нелинейно - даже для постоянных значений Ai, Qi и Di - вследствие того, что каждая популяционная переменная xi входит в выражение для средней продуктивности Е¯. Таким образом, все уравнения связываются этим членом, который дает скользящее и саморегулирующееся пороговое значение, отражающее самоорганизацию системы. Будет расти численность только тех носителей информации, "селективные ценности" W0i которых находятся выше порога Е¯. Вследствие своего роста они постоянно сдвигают порог Е¯ в сторону все больших значений, пока не достигается оптимум Е¯, равный максимальной селективной ценности всех имеющихся видов:
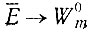 (II.32)
(II.32)или, в более общем случае (например, для осциллирующих систем), для любого периода колебаний Δt
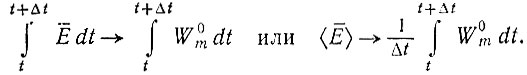 (II.34)
(II.34)В зависимости от типа реакционной системы (т. е. от связей между различными компонентами) селективная ценность W0m будет принадлежать единственному носителю информации (или вырожденному классу), если параметры Am, Qm и Dm - константы, или она может относиться к каталитическому циклу, и тогда она будет функцией концентраций всех участников цикла, или же она может относиться даже к целой иерархии реакционных циклов, что выражается в появлении концентрационных членов высшего порядка. Для нелинейных систем конечное значение W0m для любого вида носителей информации может зависеть от начальных концентраций, как, например, показывает равенство (II.21). Важно отметить, что индекс m в W0m относится к виду с "максимальной" селективной ценностью по сравнению со всеми конкурентами, присутствующими в конечной фазе. Далее, соотношения (II.33) или (II.34) являются приближениями лишь для того случая, когда членами, описывающими "исправления ошибок", можно пренебречь. В противном случае W0m можно заменить на
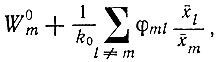
где второй член представляет собой средний "обратный поток" информации от мутантов (он может также включать в себя члены, описывающие исправление).
Когда вклад членов, выражающих исправление, мал, соотношение (II.33) в следующем приближении можно записать так:
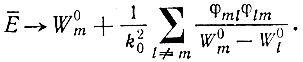 (II.33а)
(II.33а)
Это приближение пригодно до тех пор, пока второй член мал по сравнению с любой разностью 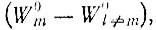 что может всегда выполняться, если Qm достаточно близко к единице.
что может всегда выполняться, если Qm достаточно близко к единице.
Таким образом, мы охарактеризовали отбор неким экстремальным принципом по аналогии с термодинамическим равновесием. Однако там мы имеем "истинный" максимум энтропии или минимум свободной энергии, тогда как здесь мы имеем дело лишь с "оптимумами", т. е. с относительными максимумами, которые получаются, если варьировать состав популяции при известных ограничивающих условиях. Мы можем также назвать состояние, характеризующееся критерием (II.33) или (II.34), "селекционным равновесием", но необходимо помнить, что здесь мы имеем дело с метастабильным состоянием равновесия. Оно стабилизирует информацию, необходимую для воспроизведения того носителя информации, который может считаться "наиболее приспособленным" в популяции, но только до тех пор, пока во флуктуирующем распределении ошибок (ср. Q < 1 и nV << N) не возникнет "селективного преимущества", характеризующегося неравенством W0m+1 > W0m. Как только появляется новая копия (или ансамбль) такого рода im+1 (ср. стохастический подход в гл. III), прежнее равновесие разрушается и система идет к новому (метастабильному) состоянию равновесия, которое характеризуется другим значением Е¯; все это в целом соответствует процедуре оптимизации. Если W0m не зависит от xi, то изменение Е¯ (при постоянных условиях окружающей среды) соответствует монотонному росту
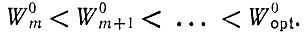 (II.35)
(II.35)Конечное состояние является "оптимальным состоянием", т. е. максимумом при ограничивающих условиях, заданных в виде неравенств. Система может тогда достигать лишь некоторых определенных состояний из полного набора N возможностей; она привязана к определенному пути, по которому вынуждена "карабкаться".
Если существуют внутренние связи, выражаемые концентрационными зависимостями параметров W0i, то весь процесс оптимизации становится более сложным. Максимум селективной ценности в популяции не имеет "абсолютного" значения, потому что он не относится теперь к данному распределению концентраций xi. В такой системе любое изменение распределения xi означает "изменение окружающей среды". Оптимизация здесь относится к "дифференциальному" процессу; она может даже сопровождаться общим уменьшением (возможно, всех) селективных ценностей (например, вследствие того, что один из отобранных носителей информации вызовет "загрязнение среды"). Она может также состоять в использовании большего количества информации (чтобы приспособиться к изменившемуся окружению). В общем процедура оптимизации в эволюции не обязательно должна представлять собой простое монотонное изменение селективных ценностей. Каким бы ни было конечное состояние, Е¯ относится здесь к максимальному значению W0 всех конкурентов, присутствующих в конечной фазе. Те виды, которые принадлежат к кооперативной системе, достигнут одного и того же значения W0m, и это равенство можно использовать для вычисления "равновесного" распределения избранных видов по аналогии с "законом действия масс".
Важно отметить, что различие между "отбором" (происходящим в данном наборе населенных состояний при фиксированных условиях среды) и "эволюцией" (дальнейшей процедурой оптимизации по отношению к изменениям популяции и среды) является абстракцией. Если рассматривать весь процесс эволюции как некую игру, то эта абстракция позволяет использовать механизм отбора как исполнительный инструмент для вычисления состояния игры согласно определенным правилам и, таким образом, заменить игрока. Эта абстракция приблизительно выполняется лишь для таких систем, где nV << N и Q близко к 1. Она требует также экспериментальных условий, которые допускают, чтобы отбор происходил за сроки, небольшие по сравнению со временем эволюционного изменения.
б) Постоянные общие потоки организованных и неорганизованных единиц
Система феноменологических уравнений имеет несколько более сложный вид, чем при ограничениях первого типа. Рассмотрим поэтому упрощенный пример, которому присущи, однако, все существенные особенности общего случая. Предположим, что все носители информации (включая ошибочные копии) имеют примерно один и тот же общий состав и скорость их образования описывается одной и той же (средней) стехиометрической функцией f(m1 ... mλ). Далее предположим, что имеется постоянный и однородный приток фМ богатых энергией мономеров (в постоянном соотношении). Тогда ограничения, введенные равенствами (II.27) и (II.28), дают
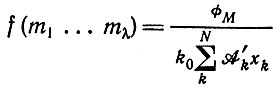 (II.36)
(II.36)и кинетические уравнения могут быть написаны по аналогии с уравнением (II.32) (пренебрегая членами "обратного потока")
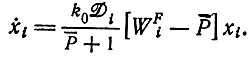 (II.37)
(II.37)Здесь Р¯ - снова средняя "продуктивность", однако она определяется как
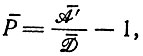 (II.38)
(II.38)
где 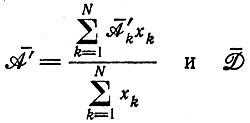 определяется соответственно.
определяется соответственно.
Как продуктивность, так и селективная ценность
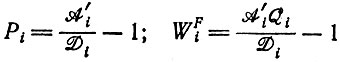 (II.39)
(II.39)относятся здесь к ограничению постоянных потоков.
Если не существует общей стехиометрической функции f(m1 ... mλ), то уравнение (II.36) можно все-таки получить формально, используя подходящие средние наряду с индивидуальными стехиометрическими членами.
Случай постоянных потоков особенно интересен в связи с применением принципа Пригожина - Глансдорфа, который обсуждался в конце гл. I. Этот принцип относится к изменению сил при постоянных потоках. Из-за наличия скользящего порога система снова выбирает максимальную селективную ценность среди имеющейся популяции. Здесь можно показать, что каждая мутация, ведущая к дальнейшему росту "селективной ценности", соответствует отрицательной флуктуации производства энтропии, указывая на неустойчивость существующего стационарного состояния. При условии постоянных потоков эволюция соответствует последовательности таких нестабильностей, когда доминирующий вид im вымирает, уступая место новому виду im+1, который имеет конечное (положительное) селективное преимущество 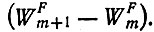
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'