§ II.2. Феноменологические уравнения

Рассмотрим класс носителей информации i_νi, каждый из которых имеется в числе x_νi экземпляров на единицу объема

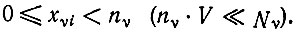(II.9)

Отбор в дарвиновском смысле должен зависеть от динамических свойств системы, которые представлены скоростями сборки и распада носителей информации. Следовательно, мы должны начать с кинетических уравнений для образования и распада макромолекул, которые описывали бы эволюционное поведение.

Для систем, далеких от равновесия, мы не можем ожидать простой линейной зависимости между потоками и силами. Таким образом, невыгодно начинать с формализма феноменологических уравнений, используемых в линейной области термодинамической теории необратимых процессов (т. е. с простых соотношений между скоростью и сродством). Поскольку было показано, что для отбора требуется совершенно особое реакционное поведение, может оказаться полезным применение терминологии химической кинетики, которая дает в более явном виде класс и порядок соответствующих реакций.

Введем три гипотезы, которые окажутся необходимыми условиями отбора:

1. Система должна быть открытой и далекой от внутреннего равновесия. Для того чтобы не дать системе прийти к равновесию, мы должны постоянно снабжать ее свободной энергией, например, в виде богатых энергией мономеров (таких, как АТФ и его аналоги по азотистым основаниям, или таких, как активированные аминокислоты). С другой стороны, распад может давать низкоэнергетические продукты. Таким образом, движущей силой обеих реакций - образования и распада носителей информации - является положительное сродство; для этих двух процессов нет соотношения типа "микроскопической обратимости", которое имелось бы вблизи от равновесия.

2. Скорость образования должна превышать скорость распада и иметь по меньшей мере тот же порядок по x_νi. Так как распад - это обычно реакция (по меньшей мере) первого порядка по x_νi^*, то реакция образования должна быть "автокаталитической". Если бы скорость образования была меньшего порядка по x_νi, чем скорость распада, система не обладала бы внутренней способностью к росту, которая необходима для отбора против менее эффективных конкурентов. В таком случае все i_νi могли бы расти только до постоянного уровня, на котором скорости их образования сравнялись бы со скоростями распада. Подобная система несла бы в себе всю бесполезную информацию предшествующих мутаций, которая в конце концов блокировала бы дальнейшую эволюцию.

^* (В реакциях распада, катализируемых ферментами, скорость реакции может стать независимой от концентрации субстрата, если фермент насыщен; однако такие реакции вовсе не делают неверным высказанное утверждение. Концентрация субстрата всегда проходит через "область ненулевого порядка" при своем росте, а конкуренция в условиях насыщения все еще зависит от популяционных переменных отдельных видов (пример дан в гл. VII).)

3. Вследствие условия n_ν⋅V << N_ν неинструктированным образованием какого-либо отдельного носителя информации можно полностью пренебречь.

В гл. IV-VI будет показано, что к автокаталитическому поведению способны многие различные классы реакций, но лишь некоторые определенные типы могут обеспечить эволюционное поведение. Одно очень важное уточнение по отношению к макромолекулярным носителям информации заключается в том, что нужно различать "самоинструктирующее" и "общее автокаталитическое" поведение. Процесс может быть автокаталитическим в том смысле, что продукт реакции стимулирует свое собственное образование - возможно, посредством какого-либо каталитического реакционного цикла, в котором участвует несколько промежуточных соединений (см. гл. V). Тогда скорость образования данного i_νi может быть пропорциональна не его концентрации x_νi, а концентрации x_νj≠i какого-то другого носителя информации, причем отношение x_νj/x_νi в конце концов достигает постоянного значения. В этом случае автокатализ является особым свойством какого-то отдельного ансамбля. Для того чтобы появились общие "матричные" свойства, необходимы "самоинструктирующиеся" носители информации. Это означает, что любая последовательность единиц инструктирует свое собственное воспроизведение. Если в процессе репродукции возникает ошибка, то ошибочная копия будет воспроизводиться дальше. Такое поведение типично для нуклеиновых кислот, тогда как "общее автокаталитическое" поведение может проявляться у белков.

Теперь можно написать в общем виде феноменологическое кинетическое уравнение для каждого носителя информации^*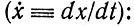

^* (В дальнейшем мы будем опускать индекс ν, кроме тех случаев, когда необходимо выделить соответствующий класс носителей информации.)

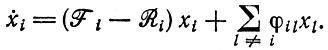(II.10)

Первый и второй члены в этом уравнении определяют скорость самоинструктированного образования носителя информации i_νi и скорость его удаления (посредством распада, разбавления и т. д.). Третий член включает в себя все другие каналы образования (не спонтанного), которое происходит в результате неточного копирования других последовательностей, близких к i_νi. Члены F_i и R_i - общие кинетические параметры, которые могут включать в себя несколько различных членов. Частная форма уравнения (II.10) выбрана такой потому, что она выражает требование наличия "неотъемлемых" автокаталитических свойств, но не подразумевает, что реакция обязательно представляет собой реакцию первого порядка. Кинетический параметр F_i, безусловно, является функцией концентраций мономеров (m₁, ..., m_λ); кроме того, F_i и R_i могут зависеть еще от x_i или от x_k - популяционных переменных других видов.

Мы можем конкретизировать F_i и R_i, пользуясь чисто феноменологическими параметрами (которые могут включать в себя сумму членов по отдельным реакциям)^*

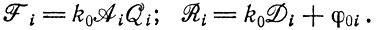(II.11)

^* (Эти конкретные символы выбраны для того, чтобы подчеркнуть общий вид параметров скорости и качества, которые могут быть сложными функциями концентраций и могут состоять из нескольких членов. [F (formation) - образование; A (amplification) - усиление; 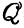(quality) - качество; R (removal) - удаление; D (decomposition) - разложение. - Прим. перев.])

Здесь k₀ - общая константа скорости первого порядка с размерностью с^-1. Она дает стандартное (или пороговое) значение констант для всех конкурентных процессов образования. При этом в размерность остальных параметров 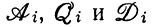уже не входит время.

Произведение A_iQ_i характеризует индивидуальную величину и форму параметров скорости образования F_i. Назовем величину A_i "фактором усиления"; k₀A_i представляет собой фактически константу скорости; эта константа показывает, с какой быстротой направляется синтез матрицей i_i. Таким образом,

учитывает все процессы образования (за единицу времени), которые инструктируются матрицей i_i, независимо от того, ведут ли они к образованию точных копий i_i или мутантов. Затем мы вводим "фактор качества" Q_i, который говорит нам, какая доля Q_i этих процессов ведет к образованию точной копии i_i. Доля (1 - Q_i) всех процессов "копирования", направляемых i_i, отвечает образованию мутантов i_j, которые частично все еще сходны с оригиналом i_i, но содержат различные ошибки, имеющие определенное распределение вероятности. Эти мутанты обычно характеризуются кинетическими параметрами ^F_j ≤ F_i, но иногда может возникнуть копия, обладающая каким-либо преимуществом (F_j > F_i).

Определения A_i и Q_i чисто феноменологические. Можно подсчитать число процессов копирования (в единицу времени), инструктированных данной матрицей, и можно определить также - по последовательности единиц или другими способами - число правильных копий i_i. Таким образом, оба параметра имеют физический смысл. Это проявляется также, если рассматривать суммарную скорость образования

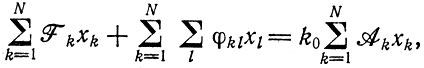(II.12)

где правая часть уже не содержит параметров качества, потому что в суммарную продукцию входит как доля точных копий Q_i, так и доля ошибочных (или мутантных) копий (1 - Q_i).

Последний член в уравнении (II.10) отражает тот факт, что любая ошибка означает образование близкой копии. Этот член может быть очень мал или им даже можно пренебречь для некоторых избранных видов, но он может быть важен для постоянного образования "свиты ошибочных копий" от отобранной главной копии. Из условия сохранения - в отсутствие спонтанного неинструктированного синтеза - получим выражение для суммарной продукции ошибочных копий:

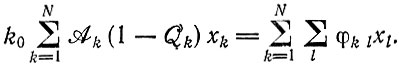(II.13)

Произведения A_iQ_i содержат также стехиометрические функции f_i(m₁, ..., m_λ), описывающие зависимость скорости образования от концентраций мономерных (богатых энергией) единиц. Их точный вид зависит от конкретного механизма полимеризации (см. гл. IV), особенно на этапе, лимитирующем скорость. Если концентрации m₁ ... m_λ забуферены - условие, которое выбирается для большинства эволюционных экспериментов (см. гл. VII), - то f_i можно включить в A_iQ_i в качестве постоянного множителя. Иными словами, можно написать

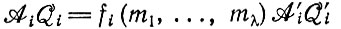(II.14)

(и, может быть, также соответствующие средние для различных ошибочных копий). 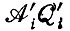не содержат больше концентрационных членов, зависящих от m₁, ... m_λ, но могут еще зависеть от концентрации x_i или от любой x_k. (f_i(m₁, ..., mλ) можно пронормировать, например, к начальным или конечным условиям.)

С помощью соотношения (II.11) для R_i мы отделили индивидуальный член D_i, описывающий разложение (который, как и член A_iQ_i, множится на общую константу скорости k₀), от члена φ_0i, который описывает разбавление и который в кинетическом уравнении множится на x_i ("пропорциональное" разбавление). В самом простом случае мы можем опустить индекс i; в этом случае φ₀ будет связан с общим потоком "разбавления" φ₀^* следующим образом:

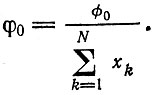
^* (φ₀ может быть также, отрицательным, если происходит "концентрирование" системы. Однако обычно член φ₀ будет использоваться для компенсации роста.)

Тогда общая скорость удаления будет равна

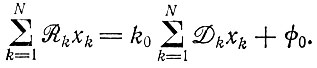(II.16)

Как уже упоминалось, параметры D_i могут быть функциями концентраций x_i или x_k, но здесь мы не можем выделить какой-либо параметр "качества", так как разложение носителей информации любого вида ведет к образованию бесполезных продуктов ("отбросов"), если не водить сложных репаративных механизмов.

Появление мутантов, вызванное не ошибками копирования, а какими-либо другими процессами, можно формально включить в те же три параметра A_i, Q_i и D_i. Тогда уравнение (II.10) примет вид

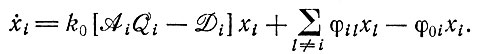(II.17)

Это феноменологическое кинетическое уравнение описывает вообще любую систему реакций, которая обладает следующими характерными свойствами:

а) метаболизмом, представленным двумя суммарными членами 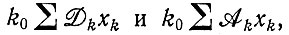которые описывают превращение высокоэнергетических веществ в низкоэнергетические;

б) способностью к самовоспроизведению, как показывает вид кинетического уравнения. Предполагается, что члены, описывающие образование и распад, пропорциональны x_i и F_i > D_i для 0 < x_i < n, какова бы ни была дальнейшая зависимость и от концентрации.

в) мутабильностью, представленной фактором качества Q_i < 1.

Оказывается, что первая часть уравнения (II.17) ответственна за способность к отбору и что A_i, Q_i и являются решающими феноменологическими параметрами. Даже для сложных "живых" существ отбор определяется этими параметрами, в которые могут входить сложные концентрационные члены, обусловленные "внутренними" связями, и которые могут зависеть от многих переменных внешней среды.

Однако в такой форме уравнение (II.17) еще не описывает процесс отбора. Оно определяет некую сегрегацию, обусловленную пороговым свойством

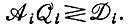(II.18)

Те носители информации, которые находятся выше порога 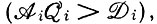будут увеличиваться в числе, а те, которые находятся ниже порога, 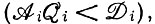будут вымирать.

Если пренебречь второй частью уравнения (II.17), то его решение можно записать в следующем общем виде:

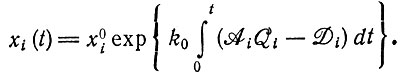(II.19)

Для постоянных A_i, Q_i и D_i это решение представляет собой вещественную экспоненту с положительным или отрицательным аргументом. Если какая-либо из этих реакций приближается к равновесию, то соответствующее решение принимает вид экспоненты с отрицательным аргументом, как показано в разд. I.2.4. Это получается с помощью разложения в ряд обратимых (в общем случае нелинейных) членов кинетического уравнения, после чего переменной становится отклонение "степени развития реакции" от равновесного значения (см. табл. 5).

Нелинейные системы могут проявить гораздо более резкое "сегрегационное" поведение. Например, дифференциальное уравнение типа

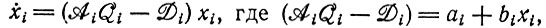(II.20)

имеет особую точку при конечном t, если 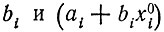больше нуля (a_i может быть даже меньше нуля). При 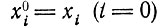мы имеем

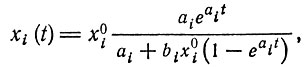(II.21)

т. е. x_i(t) стремится к бесконечности при

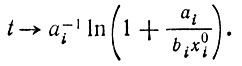(II.22)

Если a_i отрицательно, то его абсолютное значение должно быть меньше 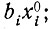в противном случае вид решения меняется. Если 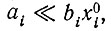решение сводится к простой гиперболе

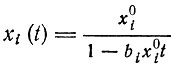(II.23)

с особой точкой при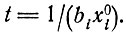

Эти и подобные им решения описывают резкое селекционное поведение (см. гл. VI) и оказываются очень важными для начала эволюции.

Я намеренно назвал описанное выше поведение "сегрегационным", а не "селекционным", потому что оно ведет только к разделению системы на две части, выделяемые пороговым свойством 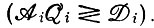Если мы хотим интерпретировать "отбор" как действие некоего экстремального принципа, то нам понадобятся не только способности к росту отдельных компонентов, но и "внешнее" селекционное ограничение, чтобы вызвать в системе настоящую конкуренцию за выживание.