Глава II. Феноменологическая теория отбора

§ II.1. Понятие "информации"

Упорядоченность в сложной системе реакций, происходящих с участием множества различных химических соединений, требует образования самовоспроизводящегося "функционального кода". Термин "функциональный код" означает наличие двух свойств: исполнительного и законодательного. Для проявления исполнительного свойства необходим аппарат, способный контролировать все реакции, идущие в системе; это может быть ансамбль взаимодействующих и саморегулирующихся катализаторов, состоящих предпочтительно из одного и того же материала, но имеющих практически неограниченные функциональные способности. Независимо от того, содержит ли первичная структура этого исполнительного аппарата инструкцию для его воспроизведения, или же она должна транслироваться из другого, законодательного источника, самоорганизация и дальнейшая эволюция коррелированного и воспроизводимого функционального поведения должна начинаться на уровне самовоспроизводящегося молекулярного кода.

Введем теперь понятие носителей кода. Тот факт, что мы знаем о существовании таких носителей кода, т. е. о нуклеиновых кислотах и белках, поможет нам создать полезную концепцию.

Введем множество, состоящее из N_ν носителей информации:

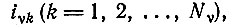(II.1)

которые представляют собой последовательности из ν единиц с базисом λ (например, λ = 4 для нуклеиновых кислот или λ = 20 для белков). Для простоты мы часто будем иметь дело с таким однородным классом носителей информации, т. е. с последовательностями, имеющими одинаковую длину ν единиц.

В классической теории информации "количество информации" в определенной последовательности i_νi выражается числом битов:

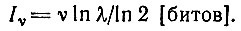(II.2)

Тогда N_ν представляет собой "структурную емкость" класса ν, т. е. число всех различных последовательностей с длиной ν и с базисом λ:

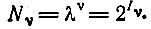(II.3)

Если последовательности могут иметь любую длину, ограниченную верхним пределом ν единиц, то мы получим

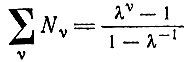(II.4)

различных последовательностей. Это число может оказаться очень важным, если мы рассматриваем системы независимых конкурентов (с любой длиной от 1 до ν), где различные последовательности представляют собой определенные сообщения (с различными "селективными ценностями", см. ниже).

Система носителей информации может находиться внутри "ящика" конечного объема, имеющего проницаемые стенки, через которые могут втекать и вытекать высоко- и низкоэнергетические мономерные единицы (рис. 3). В ящике может находиться по x_νi экземпляров каждого вида носителей информации (на единицу объема), и общая численность каждого класса составляет

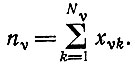(II.5)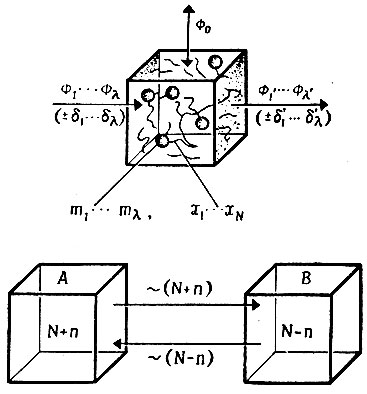

Рис. 3. 'Информационный ящик'. Предполагается, что верхний ящик имеет полупроницаемые стенки, через которые могут втекать и вытекать высоко- и низкоэнергетические мономерные единицы. Внутри ящика происходят сборка и распад последовательностей (полимеров), представляющих собой 'информацию'. Как матричная сборка, так и распад могут катализироваться ферментами. Стационарное состояние может поддерживаться регулированием потоков (ф₁ ... ф_λ; ф₁' ... ф_λ') или концентраций (m₁ ... m_λ; x₁ ... x_N), которые контролируются потоком разбавления ф₀. Для сравнения изображена равновесная система, распределенная между двумя ящиками А и В: N_A = N_B; ± n-флуктуации (обсуждение эренфестовской модели см. в § III.2)

Для большинства из N_ν возможных носителей i_νk их концентрации x_νk будут равны нулю. Концентрации неорганизованных высокоэнергетических мономерных единиц 1, ..., λ. в ящике равны m₁, ..., m_λ, а их потоки в ящик - ф₁ ... ф_λ.

Число всех единиц - организованных и неорганизованных - составляет

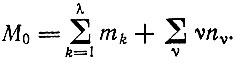(II.6)

"Степень организованности" D₀ в ящике, т. е. отношение числа организованных единиц к сумме организованных и неорганизованных единиц, равна

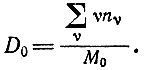(II.7)

Полная численность данного класса в объеме V практически во всех реальных случаях крайне мала по сравнению с информационной емкостью этого класса N_ν:

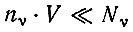(II.8)

(например, для ν = 100, λ = 20 величина n_ν⋅V может быть меньше или равна 10²⁰, тогда как N_ν = 10¹³⁰; см. табл. 3). Из этого вытекает важное следствие, что при равновероятном распределении в отсутствие самоинструктирования ожидаемое значение числа цепей с любой данной последовательностью практически равно нулю. Далее для тех последовательностей, которые образовались случайно, вероятность найти еще один случайно образовавшийся экземпляр с той же последовательностью снова практически равна нулю. Эта "ненасыщенность" информационной емкости очень важна для процедуры оптимизации в эволюции.

Наша следующая задача - придать определенные динамические свойства носителям информации и построить теорию отбора. Эта теория должна содержать вывод параметра, который выражает "селективное преимущество" через молекулярные свойства.

Для рассмотрения связанных систем можно представить себе "информационное пространство", которое задается множеством популяционных переменных x_νi и функциональными отношениями между ними. Для квазилинейных систем (истинно линейные системы неспособны "отбирать") это может привести к введению "нормальных координат", так же как в случае линейных релаксационных процессов.