
§ I.2. Предпосылки самоорганизации
I.2.1. Эволюция должна начинаться со случайных событий. "В начале" - каков бы ни был точный смысл этого понятия - по-видимому, имелся молекулярный хаос, и в гигантском многообразии химических соединений не было никакой функциональной организации. Таким образом, самоорганизация материи, которую мы связываем с "возникновением жизни", должна была начаться со случайных* событий. Из этого утверждения нельзя, однако, сделать вывод, что какие-либо, пусть даже примитивные, организмы, существующие в настоящее время, могли возникнуть в результате случайной сборки.
* (Термин "случайный" относится, конечно, к отсутствию функциональной организации, а не к отсутствию физических (т. е. атомных, молекулярных или даже надмолекулярных) структур.)
Несколько лет назад Е. Вигнер [16] написал статью "Вероятность существования самовоспроизводящейся системы", в которой он в неявной форме высказал подобное предположение. Суть его рассуждений сводится к следующему. Допустим, что состояние "живого существа", а также состояния веществ, которыми оно питается, и состояние продуктов его метаболизма полностью заданы в квантовомеханическом смысле, т. е. могут быть описаны векторами в гильбертовом пространстве. Тогда процесс воспроизведения, т. е. взаимодействие организма с питательной средой, приводящее к редупликации организма, описывается преобразованием, в которое входит унитарная "матрица столкновения" S. Если предположить, что S - случайная матрица, то оказывается, что число уравнений, задающих это преобразование, значительно превосходит число неизвестных (т. е. компонентов векторов); при этом избыток равен разности N2R - (N + R + NR), где N и R - любые большие числа. Фактически для любого реального случая N и R настолько велики, что, как правильно заключает Вигнер, "было бы чудом", если бы уравнения преобразования выполнялись для какого-то набора неизвестных (утверждение, которое остается справедливым также и в том случае, если живому организму соответствует много альтернативных состояний).
Однако все это рассуждение основано на предположении, что 5 действительно является существенно случайной матрицей и, следовательно, взаимодействие не "инструктировано", т. е. вероятность любого данного состояния ничтожно мала по сравнению с большим числом возможных состояний. Этот результат может привести только к заключению, что никакое сложное состояние материи, которое мы теперь называем живым, не может возникнуть в результате случайной сборки. Наличие инструктирования на молекулярном уровне, означающее, что матрица преобразования S должна иметь очень специальный вид, может потребовать приспособления статистической механики к описанию процессов отбора и эволюции, но это вовсе не означает, "что современные законы и понятия квантовой механики необходимо модифицировать, прежде чем их можно будет применить к проблеме жизни" [16]*.
* (В мои намерения не входило обсуждать здесь определенные трудности применения квантовой механики для описания "макроскопических процессов". Эти трудности возникают и при рассмотрении других хорошо известных физических процессов, которые не связаны с феноменом жизни. На это обстоятельство обратил мое внимание X. Примас.)
I.2.2. Инструкция требует информации. Я думаю, что именно Норберт Винер впервые предложил рассматривать информацию как новую физическую переменную. Мы имеем в своем распоряжении развитую теорию информации, начало которой положили работы Дж. фон Неймана, Н. Винера, К. Шеннона и других (литературу см. [17, 18]). Не можем ли мы воспользоваться этой теорией для решения интересующей нас проблемы самоинструктирования?
Теория информации в современном понимании - это в основном теория связи. Она имеет дело с проблемами переработки, а не "генерации" информации. Она требует, чтобы информация была задана с самого начала во вполне определенной форме. Только после этого теория может сказать нам, как закодировать сообщение и как использовать избыточность; она может также сказать нам, как согласовать сообщение с возможностями перерабатывающих устройств, чтобы передать его через каналы с шумом, отфильтровать шум и восстановить сообщение с помощью устройств, сверяющих код; однако ей всегда требуется кто-то - обычно человек, чтобы с самого начала определить, что считать "информацией" и что "бессмыслицей".
Это обстоятельство отражено уже в самом определении информации. В простейшем случае, если мы хотим отобрать ситуацию с Z1 событиями из Z0 исходных событий, имеющих равную априорную вероятность, то для того, чтобы свести Z0 возможностей к Z1, необходимо следующее количество информации:
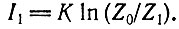 (I.1)
(I.1)Если мы хотим отобрать одно определенное событие, т. е. Z1 = 1, нужное количество информации равно
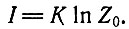 (I.2)
(I.2)Это - определение. Оно выбрано таким образом, чтобы превратить совместные вероятности (которые всегда являются мультипликативными комбинациями вероятностей отдельных независимых событий) в аддитивные величины. Так, если Z0 - число всех последовательностей длиной ν из λ различных единиц, то мы имеем
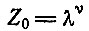
и
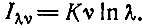 (I.3)
(I.3)Константа К выбрана в соответствии с двоичным кодом, т. е. K = 1/ln 2. Следовательно, если λ = 2, то I равняется полному числу ν двоичных единиц ("битов") в сообщении.
Итак, количество информации в последовательности из n нуклеотидов (λ = 4) составляет 2n битов. Трансляция нуклеотидного кода в аминокислотный (λ = 20) требует, чтобы единицами кодирования служили по меньшей мере триплеты. Кодирование триплетами допускает также некоторую избыточность и сигналы старта и терминации. Генетический код (табл. 2), который мы рассмотрим более подробно в гл. VI, в настоящее время полностью выяснен, в основном благодаря работам Г. Корана, X. Маттеи, М. Ниренберга, С. Очоа и их сотрудников (см. [19-21]).
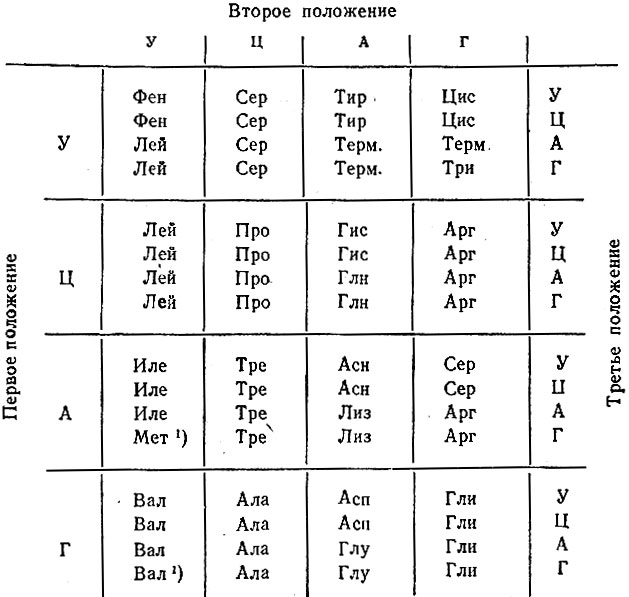
Таблица 2. Генетический код
Продолжение табл. 2
Каждая аминокислота (обозначенная начальными буквами) кодируется триплетом, составленным из оснований У, Ц, А, Г. С первого взгляда заметна существенная вырожденность в каждой клетке таблицы, указывающая на меньшее значение третьей буквы в триплете. (Подробности о замещениях в третьем положении - см. гипотезу "виляний" (гипотеза неоднозначного соответствия) Крика [22].) Заметно также некоторое сходство аминокислот в одном и том же столбце, что говорит о важном значении второй буквы. Триплеты, содержащие только У и А, дают большее число функциональных аминокислот (Фен, Лей, Тир, Иле, Асн, Лиз плюс 1 сигнал), чем триплеты, содержащие только Г и Ц (Про, Арг, Ала, Гли). Все эти факты могут содержать определенную информацию о возникновении кода и должны учитываться при построении различных теорий. Хотя код, по всей вероятности, универсален, следует оговорить, что эти соответствия (особенно "сигналы") относятся к Е. coli.
Сокращенные обозначения аминокислот:
Ала - аланин Мет - метионин*)(формилметионин) Арг - аргинин Про - пролин Асн - аспарагин Сер - серин Асп - аспарагиновая кислота Тре - треонин Вал - валин*) Три - триптофан Гис - гистидин Тир - тирозин Гли - глицин Фен - фенилаланин Глн - глутамин Цис - цистеин Глу - глутаминовая кислота Терм. - сигнал терминации Иле - изолейцин
*) (Триплеты АУГ и ГУГ означают "начало цепи", т. е. формил-Мет, если они стоят в начале цистрона; внутри цистрона они означают Мет или Вал соответственно.)
Табл. 3 очень ярко демонстрирует гигантскую информационную емкость биологических макромолекул. Вероятность воспроизводимого нахождения при любых разумных условиях (т. е. в объемах, имеющих разумные размеры), любой заданной последовательности из набора случайных последовательностей практически близка к нулю даже для относительно коротких цепей. А между тем такие последовательности не могут содержать сколько-нибудь значительного количества информации.
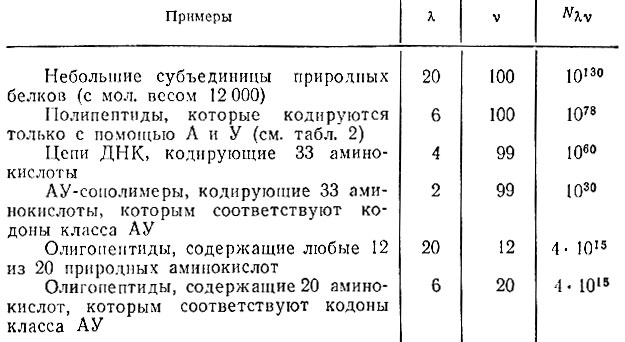
Таблица 3. Из ν единиц с базисом λ можно составить всего Nλν = λν последовательностей:
Для сравнения: число молекул белка с мол. весом 104:

Напомним, что молекулярные веса большинства природных белков и нуклеиновых кислот значительно больше, чем в приведенных примерах. Отметим далее, что возраст Земли равен "всего лишь" 1017 с, так что, даже предположив быстрый круговорот молекул белков, нельзя было бы перебрать все возможные последовательности (время жизни и продолжительность сборки каждой молекулы безусловно больше 1 с). Приведены только порядки величин. Вселенную представляем в виде сферы с диаметром 10 млрд световых лет; "плотной упаковкой" считается заполнение пространства с плотностью 1 г/см3.
С другой стороны, вся информация, содержащаяся в цепочках ДНК хромосом весьма сложного живого существа, может превышать 1010 битов, что соответствует выбору одной возможности из 103⋅109 таких возможностей. Делались попытки сопоставить подобные числа с информацией, содержащейся в тех структурах и функциях, которые кодирует ДНК. В дальнейшем будет показано, что это невозможно, если не учитывать среду и историю данного существа. Информация, накопленная в процессе эволюции, - это "оцененная" информация, и число битов мало что говорит о ее функциональном значении.
Приведенное выше определение информации потребует некоторой модификации, если мы имеем множество единиц с различными априорными вероятностями р1, р2, ..., pλ, как, например, в случае аминокислот в полипептидной цепи, или для букв в различных языках. Здесь средняя информация на единицу равна, по К. Шеннону [23, 24],
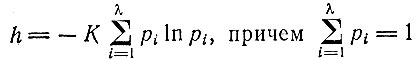 (I.4)
(I.4)(символ h выбран по аналогии с H-функцией Больцмана). Как мы видим, любое ограничивающее условие (например, различные избыточности) снижает среднее количество информации на единицу по сравнению со случаем равных априорных вероятностей. В английском языке, например, это ограничение снижает среднее количество информации с 4,76 до 4,03 бита на букву. (Другие ограничения, например наличие предпочтительных последовательностей букв или слов, будут дополнительно изменять это число.)
Аналогия между шенноновским понятием информации и больцмановской статистической интерпретацией энтропии (уравнения (1.2) и (1.4) очевидна, и всегда признавалось, что эта аналогия не только формальна [25]. В частности, это подчеркивал Э. Шредингер в своей замечательной книге "Что такое жизнь?" [26]. Если энтропия характеризует степень "незнания", то любое уменьшение "незнания" эквивалентно увеличению "знания", или "информации". Эта комплементарность между информацией и энтропией ясно показывает ограниченную применимость классической теории информации к проблемам эволюции. Везде, где информация имеет определенный смысл, например в языке (по соглашению) или в биологии (после того как эволюция привела к фиксации кода), эта теория имеет многочисленные применения. Однако от нее мало пользы, пока информация не приобрела своего "полного смысла" или пока имеется много путей создания новой информации. Здесь нам нужна новая переменная - "ценность", которая характеризовала бы уровень эволюции. Трактовка упорядоченности и неупорядоченности, указывающая лишь на их комплементарность, - на чем Э. Шредингер в своей книге сделал, пожалуй, слишком сильный упор - в этом случае недостаточна. На неадекватность современной теории информации в применении к биологическим проблемам указывал Л. Бриллюэн [18] в своей превосходной монографии "Наука и теория информации".
Мы видим, что теория информации в известной степени комплементарна классической статистической механике, по крайней мере в том отношении, что понятия энтропии и информации описывают степень незнания и знания. Для теории эволюции этих понятий недостаточно. Требуется уточнить, что мы называем знанием или незнанием. Для того чтобы охарактеризовать степень самоорганизации функциональной упорядоченности и определить направление эволюции, необходимо ввести понятие "ценности".
I.2.3. Информация возникает или приобретает ценность посредством отбора. В этом утверждении содержится один из существенных принципов биологии - дарвиновский принцип естественного отбора. Сам Дарвин считал его характерным свойством живого: "Сохранение благоприятных индивидуальных различий и изменений и уничтожение вредных я назвал Естественным отбором или Переживанием наиболее приспособленных" ([27], стр. 328).
Впрочем, Дарвин ничего не утверждал относительно физической основы этого принципа: "Возражение, что наука до сих пор не пролила света на гораздо более высокие задачи о сущности и начале жизни, не имеет значения" ([27], стр. 659).
В генетике популяций, особенно в фундаментальных трудах великих школ Р. Фишера [28], Дж. Холдейна [29] и С. Райта [30], дарвиновский принцип получил математическую формулировку. Концепция "ценности", которая стоит за этим принципом, с трудом поддается объективной физической интерпретации, что вызвало необходимость в новой интерпретации, которая будет рассмотрена более подробно в конце книги (гл. VIII, § 5). Если мы хотим уничтожить разрыв между физикой и биологией, то необходимо разобраться в том, что такое "отбор" на языке точных молекулярных понятий, которые в конечном счете могут описываться квантовомеханической теорией. Мы должны вывести дарвиновский принцип из тех свойств материи, которые нам известны.
Чтобы приблизить понятие отбора к молекулярным свойствам и пояснить его смысл, рассмотрим несколько игр с белками и нуклеиновыми кислотами.
Для введения случайности воспользуемся игральными костями: икосаэдрической - для белков и тетраэдрической - для нуклеиновых кислот. Каждая грань кости будет соответствовать одной из двадцати природных аминокислот или одному из четырех нуклеотидов. Цель игры состоит в том, чтобы, бросая кость, получить заданную последовательность из ν (например, 100) единиц: для нахождения каждого члена последовательности бросают кость и выпавшую цифру ставят на соответствующее место; если получившаяся последовательность не совпадает с нужной, весь процесс повторяют с самого начала.
Без какого-либо дополнительного правила отбора эта игра покажется довольно однообразной. Кроме тех случаев, когда ν относительно мало, она тянулась бы почти бесконечно. Мы уже видели, что для молекул белка, состоящих из 100 аминокислотных остатков, имеется примерно 10130 различных аминокислотных последовательностей, и нам пришлось бы бросать кость соответствующее число раз, чтобы получить заданную последовательность. Это просто еще один пример, иллюстрирующий вывод Вигнера о том, что ни одна белковая молекула с заданной структурой (и функцией) не могла бы возникнуть в результате случайной сборки.
Очень простая модификация правил позволит нам кончить игру за относительно короткое время. Введем отбор, придавая каждому правильно заполненному месту. некое "селективное преимущество". В предельном случае это означало бы, что правильно заполненные места дальше в игре не участвуют. Поскольку в любой случайной полипептидной последовательности (в среднем) N/20 положений заняты правильными буквами, мы видим, что теперь для получения нужной последовательности будет достаточно в среднем 20(N - N/20) = 19N бросаний (т. е. 1900 при N = 100). Флуктуации достаточно велики, чтобы у каждого игрока были равные шансы на выигрыш. Игра все еще остается довольно скучной - единственным источником азарта мог бы быть выигрыш, - но мы ясно видим действие жесткого отбора на процесс проб и ошибок. Для получения правильной последовательности требуется примерно в 20 раз большее число проб, нежели в случае полностью инструктированной сборки.
Конечно, природа играет в гораздо более изощренные игры. "Селективное преимущество" обычно не является свойством отдельного аминокислотного или нуклеотидного остатка, кроме того, оно не является независимым от состояния других положений в цепи. Эти взаимосвязи делают игру более интересной, но они требуют большего числа "ходов" и определенных стратегий. Все еще довольно простой пример такой "стратегической" игры, на этот раз с нуклеиновыми кислотами, представлен в табл. 4. Этот пример показывает, почему при сборке тРНК природа предпочла в качестве вторичной структуры конфигурацию "клеверного листа" (рис. 2). В случае нуклеиновых кислот "преимущество" обычно каким-то образом связано с наличием или отсутствием комплементарных пар оснований. В метаболизме нуклеиновых кислот комплементарность сильно влияет как на скорость синтеза, так и на скорость распада (см. гл. IV). В случае белков каталитические и регуляторные функции, зависящие от пространственной, т. е. третичной или четвертичной структуры, гораздо труднее связать с первичной структурой (последовательностью аминокислот). Все сведения, которыми мы располагаем относительно связи между структурой и функцией белков, получены в экспериментах лишь с очень немногими ферментами, детально изученными к настоящему времени (ср. [31]).
![Рис. 2. 'Клеверный лист' - модель тРНК. Дана последовательность нуклеотидов аланиноспецифичной тРНК из дрожжей (см. [5]). Необычные основания: ф - псевдоуридин, И - инозин, Н2-У - дигидроуридин, Т - риботимидин, СН3-Г - 1-метилгуанозин, (СН3)2-Г - диметилгуанозин, СН3-И - 1-метилинозин. Антикодон: 5' ИГЦ 3' (тРНК). Кодон (ГЦЦ) читается как 3' ЦЦГ 5' (мРНК)](pic/000010.jpg)
Рис. 2. 'Клеверный лист' - модель тРНК. Дана последовательность нуклеотидов аланиноспецифичной тРНК из дрожжей (см. [5]). Необычные основания: ψ - псевдоуридин, И - инозин, Н2-У - дигидроуридин, Т - риботимидин, СН3-Г - 1-метилгуанозин, (СН3)2-Г - диметилгуанозин, СН3-И - 1-метилинозин. Антикодон: 5' ИГЦ 3' (тРНК). Кодон (ГЦЦ) читается как 3' ЦЦГ 5' (мРНК)
Таблица 4. Игра в тРНК или как делать клеверные листья
Дано
Каждому игроку дается случайная последовательность из N единиц, принадлежащих к четырем классам А, У, Г, Ц, и тетраэдрическая кость, каждая грань которой соответствует одной из этих четырех букв.
Цель
Бросая поочередно кость и заполняя определенное место в последовательности выпавшей буквой, каждый игрок пытается получить двухцепочечную структуру с максимальным числом пар АУ и ГЦ.
Правила
Игра окончена, когда один из игроков объявит, что он получил "полную" структуру. Побеждает тот, кто наберет к этому времени максимальное число очков, причем за каждую ГЦ-пару засчитывается вдвое больше очков, чем за каждую АУ-пару. Пары можно образовывать только в том случае, если имеется непрерывная последовательность из не менее чем двух ГЦ-, или одной ГЦ- и двух АУ-, или же четырех АУ-пар (правило кооперативности). Соблюдая это условие, можно получать структуры любого типа (шпильки, скрепки, клеверные листья и т. п.). Для каждой петли в структуре следует оставлять неспаренными по меньшей мере 5 положений (ср. с моделью тРНК на рис. 2). Игроки бросают кость по очереди. Каждый игрок может бросить кость для любого положения по собственному выбору, однако он должен заранее объявить, для какого именно. Другое возможное ограничение: можно потребовать совпадения концов, т. е. потребовать, чтобы две концевые буквы образовали пару.
Замечание по процедуре. Может показаться удивительным, что победитель всегда получает структуру типа клеверного листа, похожую на известные вторичные структуры молекул тРНК (которые могут далее подвергнуться пространственной укладке).
"Секрет" игры состоит в том, чтобы с самого начала найти такую структуру, которая имеет максимальное число потенциальных пар оснований (включая некооперативные пары). Вероятность того, что в фиксированной структуре с n возможными парами окажется k и только k пар, можно рассчитать по формуле биномиального распределения
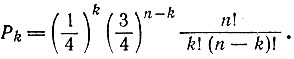
Среди всех фиксированных структур шпилька (имеющая только одну петлю) содержит максимальное число оснований, которые могут спариваться. Однако клеверный лист - структура более гибкая в том смысле, что он дает возможность испытать гораздо больше комбинаций, чем шпилька; это обусловлено тем, что отдельные листки можно сдвигать независимо от других, и мы с самого начала располагаем гораздо большим числом комбинаций. Это обстоятельство оказывается решающим. Вместе с тем при этом не может получиться слишком большое число листков, поскольку существует правило кооперативности. Для 80 нуклеотидов оптимум составляют 3-4 листка (+1 стебель). Для более длинных цепей он сдвигается к большим значениям.
Природа, видимо, играет в эту игру с давних времен. Необходимо отметить, что данное выше правило кооперативности соответствует константам стабильности, которые мы нашли для различных комбинаций оснований в олигонуклеотидах (см. гл. IV): для ГЦ-пары свободная энергия взаимодействия примерно вдвое больше, чем для АУ-пары.
Детали этой игры были разработаны Р. Винклером [51]. Количественные расчеты наиболее выгодных вторичных структур полинуклеотидных цепей были опубликованы ранее Дж. Фреско, Б. Олбертсом и П. Доти [52].
Главная цель этой работы - ввести в молекулярную динамику понятие "отбора" и связать его с уже известными нам молекулярными параметрами. Я сделал упор на относительно тривиальных примерах игр для того, чтобы показать, что правила отбора могут быть основаны на химических свойствах. Остается еще выяснить, как система могла бы использовать такие структурные преимущества и как из динамического поведения системы может следовать механизм оценивания.
I.2.4. Отбор происходит при наличии особых веществ и некоторых особых условий. Какими свойствами должна обладать материя, чтобы могла начаться самоорганизация?
Логически следует выделить несколько фаз эволюции, которые не вполне разделены во времени:
1) добиологическая "химическая" фаза;
2) фаза самоорганизации, приводящая к появлению реплицирующихся "индивидуумов";
3) эволюция отдельных видов.
Долгое время биологи имели дело главным образом с третьей фазой, которая сама по себе состоит из многих стадий: от дифференциации и возникновения пола через появление нервных клеток, автономного регулирования и способов связи до самосознания и способности к логическому мышлению, которые представляют собой уникальные свойства человеческого разума. Я не хотел бы, чтобы у читателя создалось впечатление, что переходы между всеми этими стадиями менее важны и менее ярко выражены, чем переходы между тремя стадиями, названными выше. Однако моя книга относится только ко второй фазе, к переходу от "неживого" к "живому". Как указывает Ф. Крик [32] в своем прекрасно написанном эссе "О молекулах и людях": "общеизвестно, как трудно определить понятие живого", потому что переход между живым и неживым не резкий. Таким образом, обращаясь к этому "этапу", мы должны начать с систем, которые заведомо не являются "живыми" (например, минералы), а кончить такими, из которых по крайней мере в результате развития может получиться то, что мы определенно называем "живым": бактериальные клетки, растения, животные.
Самоорганизация зависит от определенных химических предпосылок, а также от специальных условий среды. Это не "просто" свойство материи. Предбиологическая фаза - это химия и как таковая "в принципе" описывается квантовой механикой. Необходимо, конечно, показать, что условия на первобытной Земле благоприятствовали образованию нужных веществ. Другая проблема состоит в том, что в отсутствие какой бы то ни было функциональной упорядоченности возникнет гораздо большее разнообразие, чем требуется в действительности. Сложность того, чему химия может дать объяснение, огромна, загляните только в "Бейльштейна"! Все, что может возникнуть в определенных условиях, непременно возникнет; первая фаза эволюции - это фаза дивергенции, и только посредством функциональной организации она может превратиться в фазу конвергентного воспроизведения и "оцененной" эволюции.
Детальное обсуждение проблем предбиологической "химической" эволюции выходит за рамки этой работы. Этим проблемам посвящена обширная литература, и существуют прекрасные обзоры, например монография А. И. Опарина [33] - одного из первых исследователей этой области, книга М. Кальвина [34], статьи С. Фокса [35], Поннамперумы [36] и других. Две недавние статьи Ф. Крика [38] и Л. Оргела [39] заслуживают особого упоминания, потому что в них дан критический обзор - в свете экспериментальных результатов - условий возникновения второй фазы, рассмотрение которой является главной целью этой книги. Все авторы приходят к одному выводу, что основные строительные блоки биологических макромолекул - аминокислоты и высокоэнергетические фосфаты нуклеозидов (АТФ и его гомологи), а также многие другие "биохимические" соединения - могли образоваться, где это необходимо, и полимеризоваться в абиогенных условиях, например в восстановительной атмосфере и при наличии различных источников энергии. Говоря это, я не хочу создать впечатление, что все проблемы, касающиеся этой фазы эволюции, уже решены. Остаются многие вопросы, например, как возникла упорядоченная полимеризация, ведущая к образованию 3',5'-полинуклеотидов (эксперименты Г. Шрамма [40] и Л. Оргела [41] показали преобладание связей другого типа, например 2',5'-), или при каких условиях активированные аминокислоты будут полимеризоваться с образованием длинных полипептидных цепей, а не коротких олигомеров - эта проблема, вероятно, состоит в выборе подходящих каталитических условий (например, гетерогенного катализа), на что указывают недавние эксперименты А. Качальского и его группы [42]. Другая проблема - наличие достаточных количеств различных предшественников, необходимых для синтеза биологически активного материала. Решение этих проблем задаст работу еще целому поколению химиков, но это типично "химические" проблемы.
Сейчас для наших целей можно ограничиться предположением, что вещества типа высокоэнергетических фосфатов, активированных аминокислот и т. д., имелись в наличии и могли объединяться в макромолекулы, обладающие простыми каталитическими функциями, либо вследствие кооперативного действия определенных кислотных и основных групп, локализованных на боковых цепях аминокислот, либо вследствие усиления простых электронодонорных и электроноакцепторных свойств кофакторов, таких, как ионы металлов в различных валентных состояниях, либо (в случае нуклеиновых кислот) вследствие того, что они вели себя как простые матрицы.
Мы покажем, что наличие каталитических функций в сочетании с различными механизмами обратной связи, придающее системе способность к автокаталитическому росту, является одной из решающих предпосылок самоорганизации (см. гл. II).
Согласно классическому определению, катализатор увеличивает скорость прихода к равновесию, не сдвигая самого равновесия. Правда, известно, что большинство катализаторов влияет также на равновесие субстратов вследствие того, что свободная энергия их взаимодействия с субстратами не равна нулю. Однако при наличии истинного каталитического эффекта скорости прямой и обратной реакций изменяются в совершенно равной степени. Вследствие этого "автокаталитический рост" не может происходить в системе, которая находится в равновесии или вблизи равновесия. Это приводит к нашему второму вопросу: в каких условиях среды может происходить самоорганизация?
Фундаментальный ответ был дан Э. Шредингером [26], который писал: "Живая материя избегает прихода к равновесию". Равновесие (в изолированной системе) - это состояние с максимальной энтропией. Если мы удерживаем систему вдали от равновесия, мы должны постоянно компенсировать рост энтропии, т. е. "питать" систему свободной энергией или веществом, богатым энергией. Эта энергия используется для поддержания определенных реакций, которые не дают системе прийти в инертное или "мертвое" состояние равновесия. Справедливость этого утверждения очевидна, и заслуга Шредингера состоит в том, что он сформулировал его так ясно. Однако он понимал также недостаточность этого тезиса для объяснения того, "каким образом" упорядоченность поддерживается (другой) упорядоченностью и "каким образом" она сама возникла из неупорядоченности. Трудность возникает в связи с тем, что недостаточно разделить мир живого только на "упорядоченность" и "неупорядоченность".
Расширим еще немного рассмотрение термодинамического аспекта; так или иначе это понадобится для теории отбора, чтобы стоять с самого начала на твердой почве. Термодинамическая теория необратимых процессов была развита И. Мейкснером [43], И. Пригожиным [44], С. де Гроотом [45] и другими. Она основана на соотношениях взаимности Онзагера [46], которые выражают микроскопическую обратимость, и, следовательно, применялись только вблизи от равновесия. Впоследствии П. Глансдорф и И. Пригожин [47] распространили эту теорию на системы, находящиеся вблизи стационарного состояния. Для нашего рассмотрения важна не столько сама энтропия, сколько ее производная по времени dS/dt, которая состоит из двух величин: потоков, направленных из внешней среды и во внешнюю среду, т. е. deS/dt, и производства энтропии внутри системы, т. е. diS/dt; последнюю величину мы обозначим σ. Для макроскопических систем (к которым применима формула Гиббса) σ можно выразить в виде суммы членов, каждый из которых является произведением потока Ji и обобщенной силы Хi (для неоднородных систем σ необходимо проинтегрировать по всему объему, но для простоты мы не будем здесь рассматривать такие системы). Сущность теории для систем, находящихся вблизи от равновесия (где выполняются линейные соотношения между потоками и силами), выражается тогда соотношением
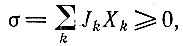 (I.5)
(I.5)т. е. энтропия всегда растет во времени для любой системы, находящейся вблизи от равновесия. В состоянии равновесия энтропия достигает максимума и σ обращается в нуль.
В табл. 5 суммированы применения теории к системам химических реакций. Каждая реакция характеризуется своей "степенью развития" ξi или ее производной
Таблица 5. Определения и формулы химической термодинамики
Сродство i-й реакции
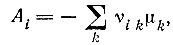
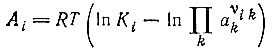
Стехиометрические коэффициенты:
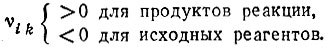
Пример: 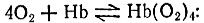
νO2 = -4; νHb = -1; νHb(O2)4 = +1.
Химический потенциал k-го вещества:
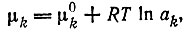 (3)
(3)μk0 - стандартный химический потенциал; ak - активность (ее можно заменить на концентрацию ck, если раствор идеален).
Константа равновесия:
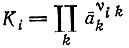 (4)
(4)a¯k относится к состоянию равновесия, где Ai = 0,
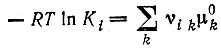
[ср. с уравнением (2)]. (5)
Степень развития (координата) реакции ξi:
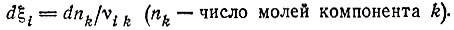 (6)
(6)При постоянных Т и Р:
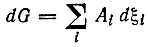 (7)
(7)(G - свободная энергия Гиббса; ξi сопряжена с Ai).
Скорость реакции:
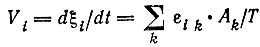 (8)
(8)(εik - феноменологические коэффициенты).
Соотношения Онзагера:
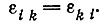 (9)
(9)Линеаризация:
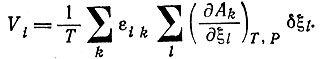 (10)
(10)
Матрицу (εik) и тензор 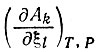 можно привести к диагональному виду. Трансформированные кинетические уравнения принимают следующий вид:
можно привести к диагональному виду. Трансформированные кинетические уравнения принимают следующий вид:
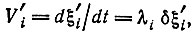 (11)
(11)
где 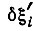 - нормальная координата, λi = - 1/τi - собственное значение, τi - время релаксации;
- нормальная координата, λi = - 1/τi - собственное значение, τi - время релаксации;
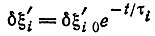 (12)
(12)- решение кинетического уравнения.
Производство энтропии:
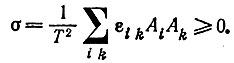 (13)
(13)по времени (т. е. скоростью реакции Vi - скалярному потоку) и "сродством" Ai (скалярной силой Ai/T). Приведенный в табл. 5 пример показывает, что вблизи от равновесия σ всегда можно выразить в виде квадратичной (положительно определенной) формы либо через величины ξi, либо через Ai. Линейное соотношение между потоками (скоростями реакций) и силами (сродством) выполняется для любой системы реакций вблизи от равновесия, независимо от порядков этих реакций или от наличия каких-либо связей между различными реакциями. Решения системы линейных дифференциальных уравнений являются экспонентами с действительными и отрицательными аргументами; иными словами, любое отклонение концентраций от их равновесных значений будет экспоненциально спадать во времени:
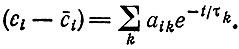 (I.6)
(I.6)Приход к равновесию - это процесс "релаксации", характеризующийся спектром "времен релаксации" τk. На протяжении последних двадцати лет исследовано много таких релаксационных спектров для очень сложных систем реакций [48]. Периодические решения (экспоненты с комплексными показателями) или неустойчивые решения (экспоненты с положительным аргументом) не встречаются; этот факт следует из соотношений Онзагера (по которым матрица кинетических коэффициентов симметрична) и знаков констант скоростей (из-за которых характеристическое уравнение является полиномом, все коэффициенты которого положительны) [49]. Различные корни - это отрицательные величины, обратные временам релаксации.
Аналогично уравнению (I.5), имеется критерий устойчивости, который выводится из классической формулы Эйнштейна для флуктуаций вблизи состояния равновесия [47]. Любая флуктуация вблизи устойчивого равновесия всегда дает отрицательное изменение энтропии
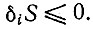 (I.7)
(I.7)Для флуктуации δξk вблизи устойчивого химического равновесия мы должны потребовать, чтобы
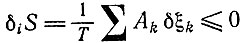 (I.8)
(I.8)или после разложения в ряд и диагонализации (Ak = 0 в равновесии)
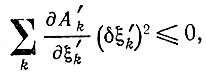 (I.9)
(I.9)так как ∂A'k/∂ξ'k < 0.
Тип решения, общий для всех систем вблизи истинного равновесия, означает, что отбор и эволюция не могут происходить в равновесных или почти равновесных системах даже при наличии нужных для этого веществ. В системах, находящихся вблизи от равновесия, автокатализ не будет приводить к росту, так как каталитическое ускорение в равной степени сказывается на прямой и на обратной реакциях.
Для систем в стационарном состоянии ограничений такого типа не существует. Как в равновесии, так и в стационарном состоянии концентрации постоянны, но эти состояния отличаются в другом аспекте. Соотношения взаимности Онзагера не выполняются в стационарном состоянии. Вследствие этого вблизи стационарного состояния могут возникнуть колебания.
И. Пригожин и П. Глансдорф [47] вывели соотношение, аналогичное уравнению (I.5), которое выполняется вблизи стационарных состояний:
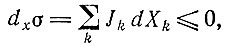 (I.10)
(I.10)т. е. изменение производства энтропии, обусловленное изменением сил Xk (например, изменение а при постоянных потоках), всегда меньше нуля вблизи стационарного состояния и равно нулю в стационарном состоянии, т. е. при варьировании сил производство энтропии минимально в стационарном состоянии системы. (Необходимо отметить, что это соотношение неприменимо для dJσ или же для dxσ + dJσ.) Здесь снова имеет место критерий устойчивости, аналогичный уравнению (I.7). Согласно этому критерию, любая флуктуация вблизи устойчивого стационарного состояния будет проявляться в "избыточном производстве энтропии"
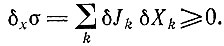 (I.11)
(I.11)Эта величина положительна и вследствие (I.10), как и в случае производства энтропии вблизи равновесия, содержит только члены второго порядка; например, для химической системы
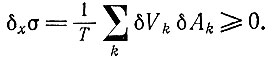 (I.12)
(I.12)Или: стационарное состояние неустойчиво, если возникает отрицательная флуктуация δxσ. Как показывает табл. 6, такую нестабильность может проявить автокаталитическая система реакций (термин "автокаталитический" ниже будет интерпретироваться в самом широком смысле). Здесь изменение скорости, обусловленное флуктуацией концентрации, и соответствующее изменение сродства имеют противоположные знаки (заметим, что это верно только вдали от равновесия, где можно пренебречь скоростями "обратных" реакций). Мы покажем, что существование таких нестабильностей является предпосылкой для селективного роста и эволюции.
Таблица 6. Пример (простой) автокаталитической реакции
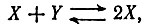
т. е. Y превращается в X,
причем X является катализатором этой реакции *)
*) (Символом X здесь обозначено химическое соединение, и его необходимо отличать от обобщенных сил Xi. Индекс х при d или δ относится к изменению сил.)
1. Вдали от равновесия
Скорость реакции:
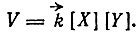 (1)
(1)При постоянной концентрации [Y]: δV ∼ δ[X].
Сродство:
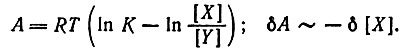 (2)
(2)Избыточное производство энтропии:
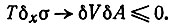 (3)
(3)В отсутствие других процессов, которые обеспечивают стабильность, такая система не может прийти к устойчивому состоянию при постоянном подводе Y.
2. Вблизи от равновесия (флуктуация δ[X])
Скорость реакции
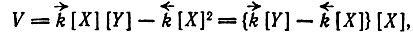 (4)
(4)
так как 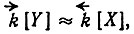 член
член 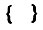 мал, а в равновесии равен нулю.
мал, а в равновесии равен нулю.
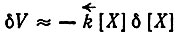 (5)
(5)(пренебрегая членами второго порядка).
Сродство: как и выше.
Избыточное производство энтропии:
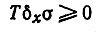
(устойчивое равновесие). (6)
Пригожин и его сотрудники показали, что сочетание автокаталитического реакционного поведения с процессами переноса может привести к своеобразному пространственному распределению реагирующих веществ. Такие распределения он назвал "диссипативными структурами", т. е. структурами, которые возникают в результате диссипации энергии, а не в результате действия консервативных молекулярных сил.
Пригожин [50] считает, что эти структуры были важны для создания функциональной упорядоченности в эволюции жизни. Они, несомненно, играли важную роль везде, где имелись благоприятные условия для их появления. Они могли оказывать некоторое влияние на ранний морфогенез, но я не думаю, что макроскопические пространственные структуры дают ключ к пониманию первых этапов биологической самоорганизации. Эти этапы могли происходить даже в бесструктурном "бульоне" при непременном участии функциональных макромолекулярных структур, таких, как нуклеиновые кислоты и белки. Тип организации, который необходим вначале, - это не столько организация в физическом (т. е. геометрическом) пространстве, сколько функциональная упорядоченность в невероятном разнообразии химических соединений, возможно находящихся в гомогенной фазе. Нам нужна организация в другом "пространстве", которое может быть названо "информационным пространством". Эта упорядоченность тоже будет основана на принципе Пригожина - Глансдорфа, которому я придаю большое значение, но его использование потребует новых параметров и может вывести нас за пределы современной термодинамической теории.
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'