
§ II.4. Селекционное равновесие
Мы назвали состояние с максимальной продуктивностью для данной популяции "селекционным равновесием". В этом "равновесии" происходят флуктуации распределения ошибок, и оно метастабильно по отношению к возникновению видов с селективными преимуществами. Тем не менее, как и в химической термодинамике, мы можем вывести "константы равновесия" из условий (II.33) или (II.34) или соответственно из их аналогов при ограничении постоянных потоков.
а) Постоянная общая организация
Средняя продуктивность Е¯ записывается как
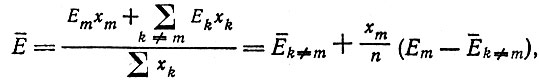 (II.40)
(II.40)где среднее значение остаточной продуктивности определяется как
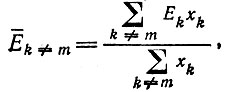 (II.41)
(II.41)если принять
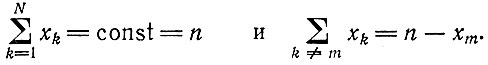 (II.42)
(II.42)Условие равновесия (II.33) тогда дает нам в первом приближении "равновесную фракцию" отобранного вида (Q ≥ 1, если пренебречь членами "обратного потока", ср. II. 6, в)
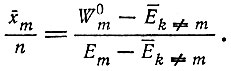 (II.43)
(II.43)Критерий отбора можно записать в виде
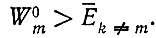
Это выражение дает физическое определение дарвиновскому термину "наиболее приспособленный".
Отметим, что относительное выживание 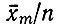 не пропорционально Qm, но стационарная ошибочная доля
не пропорционально Qm, но стационарная ошибочная доля 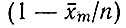 пропорциональна (1 - Qm), т. е.
пропорциональна (1 - Qm), т. е.
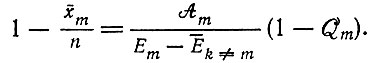 (II.44)
(II.44)
Если бы Qm равнялось единице, то W0m стало бы равно Еm и 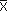 m достигла бы n. Это был бы крайний случай отбора, совершенно бесполезный, однако, для дальнейшей эволюции. "Ценность", которую приобретет такая система, ограничивается выбором из относительно узкого (случайного) набора всего лишь n видов. Мы видим также, что термин "ценность" не имеет смысла, если мы не определим, ценность "для чего". Ценность для отбора при специальных условиях уже отличается от более общей ценности для оптимальной эволюции. В последнем случае нам необходим фактор качества Qm, достаточно большой, чтобы обеспечить выживание
m достигла бы n. Это был бы крайний случай отбора, совершенно бесполезный, однако, для дальнейшей эволюции. "Ценность", которую приобретет такая система, ограничивается выбором из относительно узкого (случайного) набора всего лишь n видов. Мы видим также, что термин "ценность" не имеет смысла, если мы не определим, ценность "для чего". Ценность для отбора при специальных условиях уже отличается от более общей ценности для оптимальной эволюции. В последнем случае нам необходим фактор качества Qm, достаточно большой, чтобы обеспечить выживание
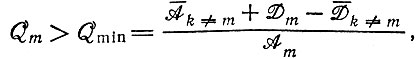 (II.45)
(II.45)но вместе с тем как можно более малый, чтобы обеспечить возникновение возможно большего числа мутантов, за счет которых мог бы происходить дальнейший "прогресс". Система должна удовлетворять очень важному условию отбора (II.45), чтобы сохранить уже накопленную информацию. Таким образом, влияние малой величины Qm (> Qm) проявляется двояким образом: во-первых, она приводит к большему разнообразию мутантов, среди которых система может отбирать, и, следовательно, позволяет прийти к более высокому конечному оптимальному значению Wm, а во-вторых, увеличивает скорость эволюции.
Селекционное равновесие в системах связанных реакций влечет за собой выживание целых ансамблей носителей информации. Здесь мы должны решать систему алгебраических уравнений. "Селективные ценности" и "продуктивности" могут стать очень сложными выражениями, содержащими все A, Q- и D-параметры связанной системы (примеры будут даны в гл. V и VI). В случае линейных систем мы можем преобразовать переменные и представить все ансамбли посредством "нормальных координат", которые ведут себя аналогично концентрациям отдельных самоинструктирующихся видов. Для некоторых нелинейных систем равновесные соотношения также можно рассчитать в явном виде. Очевидно, для таких систем термин "равновесие" имеет много общего с тем, что мы обычно называем "химическим равновесием", потому что оно связывает концентрации нескольких, а иногда даже многих компонентов. Однако различие состоит в том, что при истинном равновесии партнеры превращаются друг в друга, тогда как при селекционном равновесии партнеры собираются из одного резервуара, а разлагаются в другой резервуар, не превращаясь друг в друга; но они делают это согласованным образом, и это обеспечивает сохранение фиксированных пропорций, пока поддерживаются фиксированные условия среды.
б) Постоянный поток информации
По аналогии с равенством (II.43) мы можем вычислить равновесное отношение отобранного вида, пользуясь определениями, введенными в разд. II. 3, б, и получим (снова, как приближение для 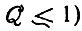
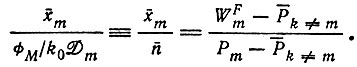 (II.46)
(II.46)
Здесь x¯m нормирована не к сумме 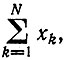 которая не инвариантна, как в случае постоянной общей организации, а к аналогичной (при данном Dm) постоянной величине
которая не инвариантна, как в случае постоянной общей организации, а к аналогичной (при данном Dm) постоянной величине
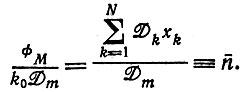 (II.47)
(II.47)
Здесь поток фМ - сохраняющаяся величина и 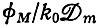 является аналогом общей концентрации. Критерий отбора снова дается неравенством
является аналогом общей концентрации. Критерий отбора снова дается неравенством 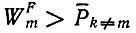 по аналогии с селекционным равновесием при постоянной организации.
по аналогии с селекционным равновесием при постоянной организации.
Селективные преимущества могут быть введены через любой из трех параметров A, Q и D, которые определяют селективную ценность. Соответственно можно различать три предельных случая (табл. 7), включающих репрессию, дерепрессию, специфичное промотирование, переваривание, которое блокируется специфичной защитой, и т. д.
Таблица 7. Критерии отбора (предельные случаи по отношению к Am, Qm и Dm)
1. 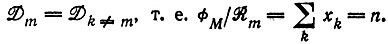
Постоянные силы и постоянные потоки
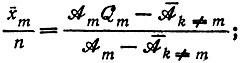
отбор, если 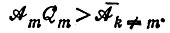
2. 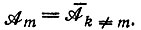
а) Постоянные силы
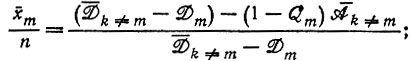
отбор, если 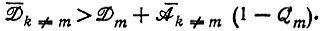
б) Постоянные потоки
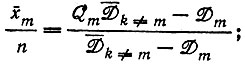
отбор, если 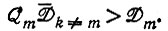
3. 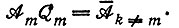
а) Постоянные силы
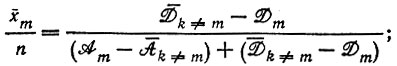
отбор, если 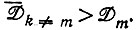
б) Постоянные потоки
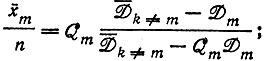
отбор, если 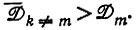
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'