
§ II.5. Фактор качества и распределение ошибок
Совершенно очевидно, что "селективная ценность" как динамическое свойство зависит от кинетических параметров, таких, как A и D. Менее очевидна роль фактора качества Q, который описывает точность воспроизведения. Для простых моделей можно в явном виде задать связь Q с такими молекулярными параметрами, как qi - точность узнавания отдельных единиц, которая выражается через измеримые свободные энергии (или параметры активации) взаимодействия при "правильном" (комплементарном) и "неправильном" (некомплементарном) спаривании отдельных единиц. Обычно при таком узнавании имеет место кооперативное взаимодействие, в котором существенна природа ближайших соседних пар (и, возможно, последующих). Это значительно увеличивает число возможных комбинаций. Пример неферментативного узнавания оснований нуклеиновых кислот А, У, Г и Ц (λ = 4) рассмотрен в гл. IV.
Если имеются всего два различных значения стабильности - одно для всех (вырожденных) комплементарных пар и другое для всех (вырожденных) некомплементарных пар, - то соотношение между феноменологическим параметром Q и молекулярным (однобуквенным) параметром узнавания q становится очень простым. Соответствующие формулы для такого случая представлены в табл. 8. Их можно обобщить для моделей, в которых имеется несколько невырожденных классов единиц (например, нуклеотиды).
Таблица 8. Фактор качества Q для модели "двух состояний"
Вероятность точного воспроизведения отдельной единицы: q.
Вероятность того, что произойдет одна из (λ - 1)-кратно вырожденных ошибок: (1 - q).
Математическое ожидание ошибки для последовательности из ν единиц:
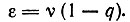 (1)
Вырожденности: 1 перестановка с 0 дефектов,
(1)
Вырожденности: 1 перестановка с 0 дефектов,
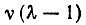 перестановок с 1 дефектом, (2)
перестановок с 1 дефектом, (2)
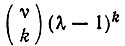 перестановок с k дефектами,
сумма:
перестановок с k дефектами,
сумма: 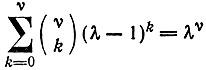 возможных (3)
последовательностей (ср. табл. 4).
возможных (3)
последовательностей (ср. табл. 4).
Вероятность возникновения копии, не содержащей ошибок:
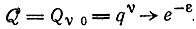 (4)
(4)Распределение вероятностей для возникновения последовательностей с k и только с k дефектами:
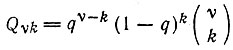
(биномиальное распределение), (5)
для 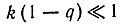 оно аппроксимируется распределением Пуассона:
оно аппроксимируется распределением Пуассона:
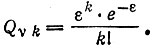 (6)
(6)Сумма ошибочных копий:
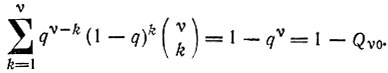 (7)
(7)Вероятность возникновения одного определенного мутанта, содержащего k ошибок в определенных положениях:
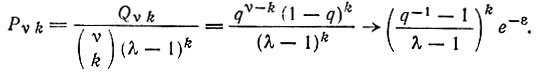 (8)
(8)Скорость продукции данного мутанта (например, с каким-то селективным преимуществом) пропорциональна Pν k. Распределения вероятностей (5), (6) и (8) показаны на рис. 4.
Минимальное значение Qν 0 для стабильного отбора определено уравнением (II.45). При данном значении фактора узнавания q критерий стабильного отбора приобретает вид
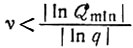 (9)
(9)или, если (1 - q) << 1,
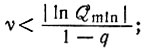 (10)
(10)тем самым определяется предельное количество информации Imax, которое может правильно воспроизводиться и сохраняться в системе.
Смысл Q как фактора качества иллюстрирует график распределения ошибок (рис. 4). Чем меньше ожидаемое значение ошибки, тем круче становится соответствующая кривая Q, т. е. тем выше фактор "качества". Важный критерий эволюции, уравнение (II.45), связывающее "разброс" кинетических параметров с минимумом фактора качества Qmin, определяет максимальное количество информации νmax, которое может сохраняться в процессе воспроизведения при фиксированном значении параметра узнавания q [ср. с уравнением (10) в табл. 8]:
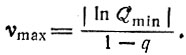
![Рис. 4. Распределения вероятностей появления ошибочных копий. Qvk вычислены по уравнению (5) в табл. 8. Значения параметров: Две кривые для q3 даны для сравнения биномиального распределения с распределением Пуассона [уравнения (5) и (6)]. Для q1 и q2 при малых значениях k эти кривые совпадают (в пределах точности графика). Однако, когда k - v, возникают большие различия. Кривые имеют максимумы при k = e. В линейной шкале эти распределения убывали бы крайне резко. Распределение Pvk из уравнения (8) на графике не изображено, потому что оно слишком резко убывает с ростом k. Например, для q](pic/000151.jpg)
Рис. 4. Распределения вероятностей появления ошибочных копий. Qνk вычислены по уравнению (5) в табл. 8. Значения параметров:
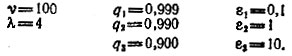
Две кривые для q3 даны для сравнения биномиального распределения с распределением Пуассона [уравнения (5) и (6)]. Для q1 и q2 при малых значениях k эти кривые совпадают (в пределах точности графика). Однако, когда k → ν, возникают большие различия. Кривые имеют максимумы при k = ε. В линейной шкале эти распределения убывали бы крайне резко. Распределение Pνk из уравнения (8) на графике не изображено, потому что оно слишком резко убывает с ростом k. Например, для q.

Вследствие этого элементарный механизм узнавания (т. е. q) должен улучшаться с ростом информационного содержания Iν носителя информации в ходе эволюции.
На высших ступенях молекулярной эволюции требуются очень сложные контрольные механизмы, чтобы увеличить точность узнавания отдельных букв (например, ферментативная проверка кода) и для того, чтобы значения параметров A и D могли варьировать в достаточно широких пределах (см. гл. IV-VI).
Цель этого обсуждения состояла в том, чтобы показать значение фактора качества не только для отбора в данной популяции, но и для скорости дальнейшей эволюции и для конечного оптимального состояния. В популяции, характеризующейся сравнимыми значениями кинетических параметров, система выбирает высокие значения Q, а это, по-видимому, неблагоприятно для скорости дальнейшей эволюции. С другой стороны, высокие значения Q делают возможным образование видов с большим информационным содержанием, что в конечном счете оказывается благоприятным для дальнейшей эволюции. Мы видим, что процесс оптимизации может иногда совмещать противоречивые требования. Например, специфичное узнавание субстрата ферментом требует высокой константы стабильности для фермент-субстратного комплекса, но слишком высокие константы стабильности ограничивают скорость оборотов фермента. Эта проблема оптимальной эволюции, возникающая в результате обобщения концепции ценности, обсуждается в гл. VIII. Уже здесь мы видим, что "ценность" всегда требует спецификации оцениваемого свойства и, чем выше уровень эволюции, тем более необходима эта спецификация.
Существенный результат этого обсуждения состоит в том, что Imax - максимальное количество информации 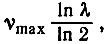 которое может сохраняться при воспроизведении, - должно зависеть от точности узнавания элементарной единицы. Эта величина, определяемая изменением параметров A и D, входит только как логарифмический член и поэтому должна оказывать ограничивающее влияние только в случае малых изменений A
которое может сохраняться при воспроизведении, - должно зависеть от точности узнавания элементарной единицы. Эта величина, определяемая изменением параметров A и D, входит только как логарифмический член и поэтому должна оказывать ограничивающее влияние только в случае малых изменений A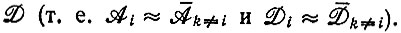
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'