§ II.6. Кинетика отбора

Феноменологические уравнения с рассмотренными типами ограничений всегда представляют собой системы нелинейных дифференциальных уравнений. Явные решения, конечно, зависят от специального вида уравнений, который в свою очередь определяется конкретным механизмом реакции. Некоторые механизмы для самоорганизующихся систем, содержащих белки и нуклеиновые кислоты, будут обсуждаться в гл. IV-VI. Здесь мы будем иметь дело только с некоторыми прототипами решений для постоянных параметров W_i, чтобы охарактеризовать процесс отбора. Рассмотрим три случая в порядке возрастания сложности:

а) Постоянная общая организация

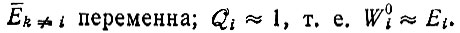
Точное решение системы дифференциальных уравнений (II.32) может быть дано только в том случае, если полностью пренебречь членами 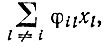т. е. потоком информации в мутантные копии и из них В этом случае система уравнений упрощается:

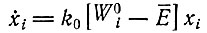(II.48)

и имеет следующее решение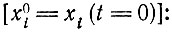

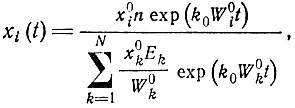(II.49)

где любое W⁰_k можно также заменить на E_k.

Это решение можно получить, исходя из неявной формы, которая получается при интегрировании (II.48):

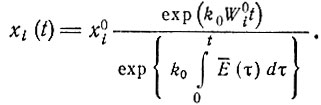(II.50)

Интегральный член исчезает для любого отношения (x_k/x_i), которое можно ввести в выражение для Е¯, если записать его следующим образом:

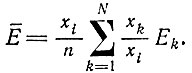(II.51)

Тогда кинетическое уравнение (II.48)

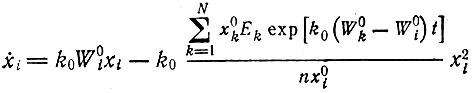(II.52)

представляет собой специальную форму дифференциального уравнения Бернулли

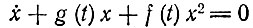(II.53)

с хорошо известным решением [54]

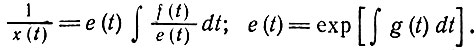(II.54)

Подстановка

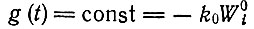(II.55)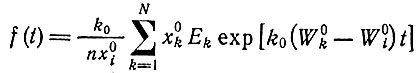

дает решение (II.49).

Это решение описывает в явном виде процедуру отбора. При t = 0 каждое x_i равно своему начальному значению x⁰_i. При t → ∞ сумма экспонент может быть представлена ее наибольшим членом, который принадлежит виду с наибольшей "селективной ценностью": W⁰_m. Этот вид отбирается. Его концентрация стремится к стационарному значению

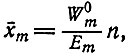(II.57)

которое равно n, если 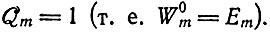Все другие виды должны в конце концов исчезнуть в соответствии с уравнением

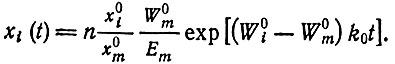(II.58)

Прежде чем x_m достигнет своего "доминантного" уровня, некоторые x_i(t) могут сначала увеличиться в числе и пройти через максимум и лишь после этого исчезнуть. На рис. 5 приведен пример с четырьмя конкурирующими видами.

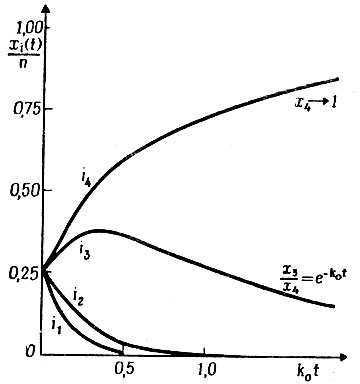
Рис. 5. Отбор в системе четырех конкурирующих видов по уравнению (II.49).

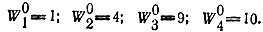
Этот подход все еще может дать полезное решение для главной копии, если Q_m не точно равно, но близко к единице. Когда отобранная главная копия достигнет доминирующего уровня, она будет конкурировать преимущественно с мутантами, возникающими вследствие неточного воспроизведения. Изложенный подход не описывает поведения этих мутантов, для которых в соответствии с равенством (II.13) необходимо учитывать дополнительные члены (особенно φ_imx_m) в кинетических уравнениях. Их концентрации, следовательно, не упадут до нуля. Для отобранной главной копии выражениями. 49) и (II.57) дают хорошее приближение, пока 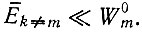Здесь мы не уточняем вида ошибочных копий, а просто имеем в виду, что какое-то число ошибок существует. (Если W⁰_m = E_m, т. е. Q_m = 1, система не может развиваться дальше.) Прежде чем рассматривать более подробно взаимодействие между главной копией и мутантами, мы можем заняться специальным случаем, когда можно дать простое решение для Q_i ≤ 1.

б) Постоянная общая организация или постоянные потоки

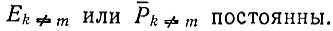
Этот случай описывает либо конкуренцию между двумя видами m и k, либо конкуренцию с целым вырожденным классом видов k ≠ m, в котором E_k≠m или P_k≠m постоянны. Мы видим также, что этот случай представляет собой хорошее приближение для отбора в системе видов, которые не вырождены по E_k≠m или P_k≠m, но дают довольно постоянное распределение вокруг средних значений 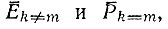в то время как отобранный вид имеет другую скорость воспроизведения с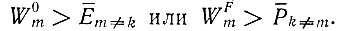

В случае постоянной общей организации решение для отобранного вида следующее:

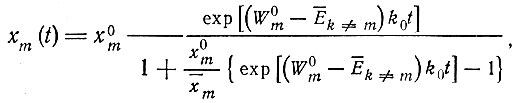(II.59)

где

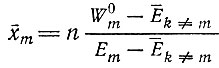
[ср. с равенством (II.43)]

- "равновесное" значение x_m (в соответствии с определением § II.4), которое достигается при t → ∞. Опять все "независимые" виды с 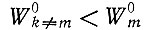в конце концов вымирают, тогда как сумма по всем мутантам (вырожденным в соответствии с допущением 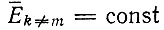доходит до стационарного уровня [ср. с равенством (II.44)].

Существует еще одно ограничение по отношению к Q_m: оно не должно быть слишком мало, чтобы можно было пренебречь повторным появлением вида im из мутантов (в результате исправления ошибок при последующих воспроизведениях). Допустимый диапазон значений Q_m зависит здесь от количества информации, т. е. от числа единиц ν в цепи. Это же ограничение имеет место также для "равновесного" значения, согласно уравнению (11.43). В другие случаях уравнение (II.43) служит хорошим приближением для конечной фазы отбора в пределах одной популяции, где имеет место практически только конкуренция между мутантами (и главной копией). Здесь среднее значение E¯_k≠m действительно может быть аппроксимировано константой, так что это решение воспроизводит правильное "равновесное" значение x_m (и сохраняет силу также в окрестности селекционного "равновесия"). С другой стороны, решение (II.49) (первый случай) не приводит к правильному равновесному значению, за исключением ситуации, когда 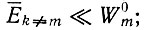но это хорошее приближение для начальной фазы отбора, когда число мутантов мало по сравнению с числом неродственных копий. Решения, подобные (II.59), но с Q = 1, неоднократно обсуждались в литературе по генетике популяций [55]. Известный случай - уравнение Росса для распространения малярии [56]. А. Лотка дал также общие математические критерии устойчивости решений таких уравнений [57].

Явное решение задачи о конкуренции между "двумя видами" можно получить также в случае ограничения постоянных потоков, предположив, по крайней мере, одну и ту же стехиометрию f(m₁ ... m_λ) для всех видов (такое же допущение мы делали раньше в связи с выражениями (II.36) и (II.46). В кинетическом уравнении (II.37) члены 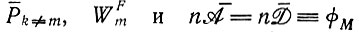являются константами (в предположении, что образование и распад подчиняются кинетике первого порядка), в то время как члены 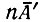и, следовательно, 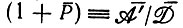являются линейными функциями x_m. Индивидуальные кинетические уравнения, имеющие вид

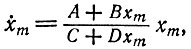(II.60)

где

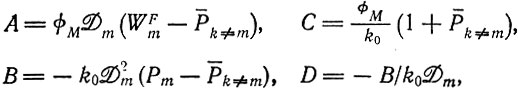
можно проинтегрировать и получить следующие альтернативные решения:

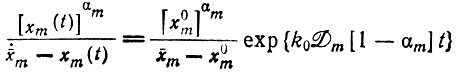
или

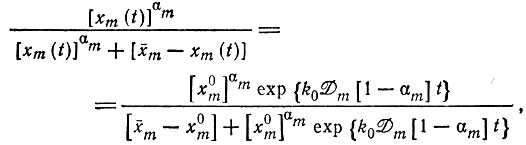(II.61)

где

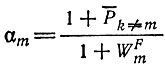
или

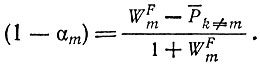(II.62)

Это решение ведет себя очень сходно с решением (II.59). При t → 0 численность "отобранного" вида растет по закону

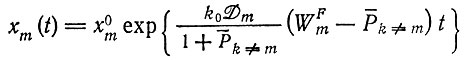(II.63)

(приближение для тогда как при t → ∞ x_m(t) стремится к "равновесному значению"

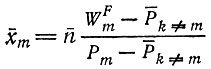[ср. с (II.46)].

в) Постоянная общая организация

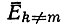
переменно; приблизительный учет продукции ошибок: Q < 1 (но не << 1).

По мере роста численности отобранного вида воспроизводимо возникающие мутанты главной копии отдают все больший вклад в общую продукцию. Эти мутанты можно разделить на классы согласно числу дефектных положений (по сравнению с главной копией), т. е. 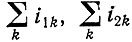и т. д. Для последовательностей длиной ν единиц число копий в каждом классе дается биномиальными коэффициентами, причем для Я типов единиц каждый дефект в данном положении (λ - 1)-кратно вырожден; так, мы имеем 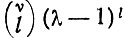различных копий в классе с l дефектами. Частота продукции отдельных копий i_lk убывает с увеличением l: например, в рамках простейшей модели, предполагающей равные q-факторы для узнавания отдельных единиц (ср. с табл. 8), эта частота пропорциональна

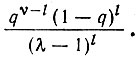
Соответственно каждый класс дефектов будет давать вклад в восстановление главной копии, причем этот вклад убывает с увеличением числа дефектов.

Для того чтобы получить некоторое количественное представление о влиянии мутантов на отбор, рассмотрим упрощенный случай - влияние единичных дефектов. Это приближение пригодно лишь до тех пор, пока математическое ожидание ошибки ν(1-q) остается значительно меньше единицы, т. е. 0 << Q < 1.

Тогда мы должны различать три класса кинетических уравнений (W ≡ W⁰ всегда относится к постоянной организации).

а) Для одной главной копии i_m

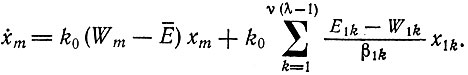(II.64а)

б) Для ν(λ - 1) мутантов i_1i, имеющих один однобуквенный дефект,

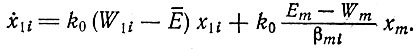(II.64b)

в) Для 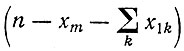независимых конкурентов i_ji

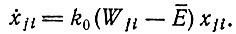(II.64с)

Третью категорию независимых конкурентов можно считать также мутантами главной копии, имеющими j ≥ 2 дефектов. Для достаточно длинных последовательностей это число возможных конкурентов так велико, что вероятность случайно найти любую данную копию практически равна нулю. Предполагается, что их возникновением в результате мутаций главной копии можно пренебречь. Это относится и к тем мутантам главной копии, которые имеют дефекты только в двух положениях. Далее, приближение требует (до тех пор, пока независимые конкуренты дают существенный вклад в решение), чтобы

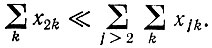(II.65)

Факторы β в уравнениях (II.64а) и (II.64b) в общем случае связывают продукцию данного мутанта с общей продукцией дефектов, которая равна

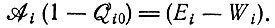
В случае одинаковых значений 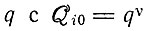и равных скоростей продукции ошибок β_mi, например, сводится к

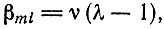(II.66)

так как доля 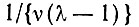всех ошибок, возникших при воспроизведении главной копии, будет соответствовать продукции любой однодефектной копии.

Для того чтобы получить самосогласованное приближение, мы должны пренебречь всеми мутациями, кроме возникновения единичных дефектов в главной копии и восстановления главной копии из однодефектных копий. Это заставляет допустить, что W_ji ≈ E_ji, (E_1k - W_1k) = A_1k(1 - q) и β_1k = 1. Последнее предположение, т. e. замена Q на q для всех однодефектных копий, кажется на первый взгляд несколько нереалистичным, так как оно допускает только один сорт ошибки, а именно тот, который ведет к восстановлению главной копии. Однако пренебрежение другими ошибками при воспроизведении однодефектных копий (которые могли бы дать копии с двумя дефектами) согласуется с этим приближением и влияет только на малые поправочные члены. Для любой из отдельных копий i_1k различие между Е_1k и W_1k пренебрежимо мало; однако в этом приближении надо учитывать сумму всех этих членов в уравнении (II.64а).

Для главной копии мы получим следующую зависимость концентрации от времени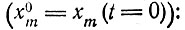

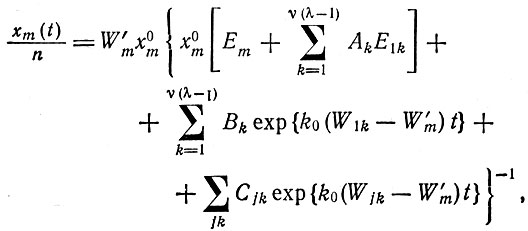(II.67)

где

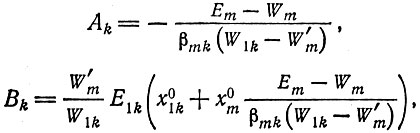(II.68)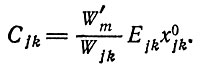

W'_m можно выразить как

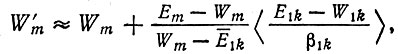(II.69)

где символ < > означает "равновесное среднее", взятое по всем ν(λ - 1) однодефектным копиям. Можно видеть, ЧТО W'_m сводится к W_m при Q_m → 1. При t → ∞ решение стремится к равновесному отношению [ср. с уравнением (II.43)]

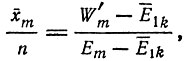(II.70)

где любой остаточный член пренебрежимо мал в рамках настоящего приближения, которое требует, чтобы главная копия отличалась достаточно большим селективным преимуществом: W'_m > W_1k.

Насколько мала разница между W'_m и W_m, можно видеть из модели, предполагающей одинаковую точность узнавания единиц, которая дает

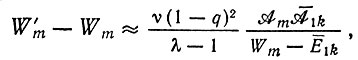(II.71)

где (1 - q) << 1/ν. (Отметим, что в этой модели средние 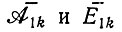занимают место прежних средних 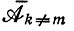и

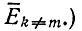
Решения для однодефектных копий i_1i и для независимых конкурентов i_ji связаны с решением для главной копии следующими соотношениями:

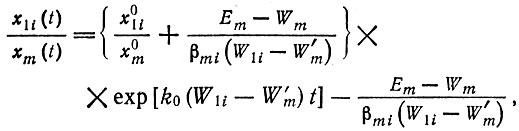(II.72)

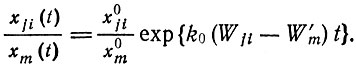(II.73)

Для получения этих явных решений, относящихся к отдельным видам, было сделано предположение, что прежде чем главные копии перерастут конкурентов, между ними и мутантами устанавливается "равновесие", так что в (малом) поправочном члене уравнения (II.64а) отношение

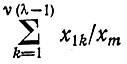
можно заменить (постоянным) равновесным отношением. При этом кинетическое уравнение для главной копии упрощается:

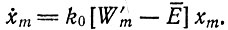(II.74)

Здесь W'_m отличается от W_m только членом, который остается малым, пока сумма 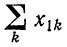мала по сравнению с x_m (т. е. (1 - Q_m) << 1). Дальнейшая процедура аналогична случаю "а", Легко находим выражение для x_1i/x_m, причем

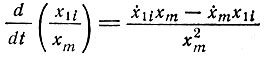
берем из уравнения (II.64); формулу для x_ji/x_m находим аналогичным образом. Эти отношения используются для выражения Е в форме (II.51), и после подстановки в (II.74) для x_m получается дифференциальное уравнение типа Бернулли. Интегрирование можно провести по аналогии со случаем "а".

До сих пор наше обсуждение ограничивалось теоретическим рассмотрением самоотбирающихся реакционных систем, но не каких-либо реальных приложений. Для них удовлетворительные решения всегда можно получить с помощью ЭВМ. Предыдущее рассмотрение показывает нам, до какой степени мы можем использовать простые приближения. На самом деле простая линейная форма первичных кинетических уравнений применима лишь для очень немногих систем реакций. В общем случае нам придется учитывать различные взаимодействия, сначала между "информационными" и "функциональными" молекулами, а затем также между индивидуальными членами этих классов. Это может привести к возникновению циклов или сетей реакций, причем поведение каждого отдельного участника реакции будет описываться нелинейными кинетическими уравнениями (например, типа уравнения Михаэлиса - Ментен или даже более сложными). Эти более реалистичные системы будут детально рассмотрены и сопоставлены с экспериментальными результатами в гл. IV-VI. Мы увидим, что характерные свойства процесса отбора, вытекающие из теории, изложенной в этой главе, четко воспроизводятся в более сложных системах, хотя явные решения могут обнаруживать важные качественные отличия - возможны колебания различных типов или наличие особых точек, дающих очень резкий отбор. Мы увидим также, что эти качественные различия окажутся очень важными в связи с обсуждением проблемы возникновения самоорганизующихся "живых" систем.