§ V.3. Могут ли белки воспроизводить себя?

Результаты, приведенные в предыдущих параграфах, подсказывают отрицательный ответ на этот вопрос.

Белки имеют два свойства, которые на первый взгляд делают их даже более пригодными, чем нуклеиновые кислоты, для инициирования самоорганизации:

1) значительно большую точность узнавания определенных субстратов благодаря наличию у белков третичной структуры,

2) большее количество информации, содержащееся в многочленном цикле (с ветвями), по сравнению с информационной емкостью одной цепи, имеющей ограниченную длину.

Недостаток состоит в том, что отдельный белок не может воспроизвести длинную цепь из одиночных звеньев и, кроме того, способность к специфичному узнаванию не представляет собой неотъемлемое свойство "любой" цепи - напротив, это уникальное свойство лишь "определенных" цепей или же редкое совпадение специальных функциональных свойств различных цепей. Вследствие этого белки, которые катализируют свое собственное воспроизведение посредством специфичных циклов, не будут автоматически воспроизводить мутантов, возникающих в результате ошибочного копирования, даже если эти мутанты обладали бы каким-то преимуществом.

Поскольку белки в качестве самовоспроизводящихся молекул обладают как преимуществами, так и недостатками, этот вопрос следует проанализировать более детально.

Было показано, что независимые каталитические циклы являются "самоинструктирующимися", подобно способным к самоинструктированию или комплементарному инструктированию отдельным молекулам, таким, как молекулы нуклеиновых кислот (которым в отличие от белков это свойство присуще изначально). Хотя в настоящее время мы не знаем, существует ли в природе такая самоподдерживающаяся сеть белков - за исключением системы биосинтеза некоторых антибиотиков типа грамицидина S (хотя и в этом случае ферменты, участвующие в биосинтезе, генетически закодированы), - во всяком случае можно представить себе возможность искусственного построения подобной сети.

Какова вероятность самопроизвольного образования таких циклов? Если взять только функцию катализа образования пептидных связей между различными аминокислотами, то можно сказать, что в наборе случайных последовательностей определенная их доля будет всегда проявлять такую каталитическую активность. Весь процесс образования белковоподобных веществ со случайными последовательностями, таким образом, уже является автокаталитическим. Это оказывается существенной предпосылкой для эволюции живых существ, и важно отметить, что это может происходить без инструктирования, осуществляемого нуклеиновыми кислотами.

Однако для эволюционного поведения случайного автокаталитического роста недостаточно. Система может улучшаться только в результате использования селективных преимуществ, а это требует спецификации последовательностей. В гл. I было показано, что вероятность случайного появления нескольких точно совпадающих последовательностей слишком мала, чтобы иметь какое-либо значение. С другой стороны, только оптимально адаптированные ферменты (какими они нам известны в настоящее время) представлены уникальными последовательностями. Система вполне может начать с далеко не оптимальных качеств функционирования, и для этого может оказаться достаточно спецификации относительно немногих стратегических положений в последовательности. Специфичная функция может проявляться - в гораздо большей степени, чем у современных ферментов, - у относительно широкого класса различных последовательностей, у которых совпадает только ограниченное число звеньев.

Допустим, что имеется достаточно большое число функциональных белков, которые катализируют образование других белков из предшественников. Пусть каждому из этих белков поставлена в соответствие некоторая точка. Соединим линиями те точки, которые каталитически связаны. Предположим, что для каждой из этих точек имеется одна и та же априорная вероятность p того, что она будет мишенью для каталитической активности другой данной точки. Таким образом, для непрерывной петли, включающей k точек, соответствующая вероятность равна p^k. Общее число k-членных замкнутых петель равно 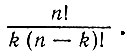Выражение 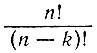дает число всех возможных комплексий, отличающихся выбором и последовательностью элементов (т. е. это число всех перестановок из n элементов по k).

Поскольку мы рассматриваем циклические расположения, эти перестановки k-кратно вырождены (начало и конец цикла могут находиться в любом из k положений, например DABC и ABCD и т. д.). Следовательно, вероятность возникновения любого k-членного цикла равна

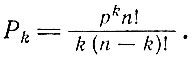(V.14)

При больших n и (n - k) можно применить формулу Стирлинга

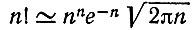(V.15)

и получить выражение для максимального значения Р_k (из условия ∂P_k/∂k = 0)

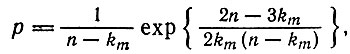(V.16)

откуда следует, что k_m близко к n для любой, 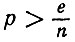и приближается к единице для р < 1/n.

Следовательно, можно сделать вывод, что при больших n (когда р >> 1/n) будут образовываться большие петли со многими соединениями, в которых будут участвовать почти все каталитически активные белки.

Вся эта процедура, предполагающая одинаковые априорные вероятности существования каталитической связи, может оказаться сомнительной, потому что при этом допускается грубое упрощение очень сложной ситуации, для точного описания которой необходима гораздо более детальная информация, чем та, которой мы располагаем сейчас. Специфическая корреляция определенных последовательностей с определенными репродуктивными функциями вполне возможна, но эти функции не будут представлять собой неотъемлемое свойство структуры, как это было в случае нуклеиновых кислот, где данная последовательность всегда индуцирует воспроизведение самой себя. У белков такая априорная корреляция между последовательностью и репродуктивной функцией отсутствует, так что выводы о воспроизводящихся петлях остаются качественно верными. Каждая связь, конечно, характеризуется своими кинетическими параметрами, выраженными в селективных ценностях W_i. Вероятность существования данной связи уменьшается с увеличением W_i. Таким образом, в действительности следует использовать понятие плотности распределения вероятностей p(W) и определить вероятность p(W)dW существования связи в интервале селективных ценностей от W до W + dW. Такая спецификация требуется в том случае, когда различные петли, характеризующиеся различными селективными ценностями W_i, подвергаются действию отбора. В этом случае каждая петля с большим значением W_i окажется связанной со многими (более протяженными) петлями, имеющими меньшие селективные ценности, будучи лишена возможности "освободиться" от них в результате отбора.

Один из крупных недостатков простых воспроизводящихся петель состоит в том, что они не могут освобождаться в процессе отбора от паразитных связей, функционирующих менее эффективно.

Каталитические циклы имеют еще один, в эволюционном аспекте даже еще более серьезный недостаток. Предположим, что имеется независимый цикл, который отбирается среди своих конкурентов.

Казалось бы, этот цикл (рис. 15) может эволюционировать в результате возникновения мутаций, т. е. вследствие неточного воспроизведения одного из ферментов, участвующих в цикле. Пусть Е'₁ - такой мутант. Тогда того условия, что Е'₁ - "лучший" катализатор, чем Е₁, недостаточно для эволюции, потому что Е₂ ... Е_n снова воспроизведутся, но это снова приведет к Е₁, а не к Е'₁. Чтобы цикл улучшился, должна произойти цепь специфичных мутаций Е'_' → Е'₂ ... Е'_n → Е'₁, т. е. должен образоваться новый специфичный цикл. Но вероятность того, что произойдет цепь заданных событий, гораздо меньше, чем вероятность появления "какого-нибудь" k-членного цикла (для рис. 15: из равенства (V.14) видно, что p^k мало по сравнению с P_k).

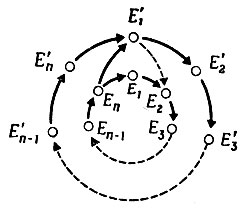
Рис. 15. Воспроизведение мутантов в каталитическом цикле

До сих пор мы описывали каталитические сети при помощи линейных кинетических уравнений, хотя при общих условиях (например, когда концентрации некоторых участников реакции непостоянны) уравнения должны быть нелинейными. Более того, на поведение, которое описывается кинетическими уравнениями (V.1), могут накладываться нелинейные эффекты. Возникает вопрос, придется ли при учете нелинейных эффектов внести какие-либо качественные изменения в существенные выводы. Мы безусловно увидим качественное изменение решений (см., например, следующие параграфы). Однако основной вывод о том, что такие системы не могут эволюционировать из-за отсутствия у белков внутренне присущей им способности инструктировать свое самовоспроизведение или комплементарное воспроизведение, остается в силе и даже приобретает еще большее значение для нелинейных каталитических цепей, способность которых к воспроизведению опять-таки является результатом наличия целого набора уникальных макромолекулярных последовательностей. Такая система не может легко использовать "селективные преимущества", потому что она нагружена слишком большим количеством "информации с низкой селективной ценностью". Линейное приближение селекционного поведения достаточно хорошо иллюстрирует это положение.