§ V.2. Самоорганизующиеся циклы ферментов (теория)

V.2.1. Каталитические сети. Исходя из свойств, описанных в § 1, можно построить "каталитическую сеть" (рис. 12). Некоторые входящие в нее белки обладают способностью катализировать конденсацию ограниченного числа аминокислот в цепи с определенными последовательностями (например, до определенных пентапептидов); другие такие "ферменты" узнают данные концевые последовательности этих олигопептидов и соединяют их в более длинные цепи, так что в конце концов могут возникнуть цепи любой длины. Ферменты, обладающие такими каталитическими функциями, обычно полифункциональны. Они могут узнавать определенные последовательности, принадлежащие различным полипептидным цепям (имеющим различную длину), причем их действие зависит также от конкретной третичной структуры субстрата и доступности узнаваемого участка, который не должен быть спрятан внутри свернутой полипептидной цепи.

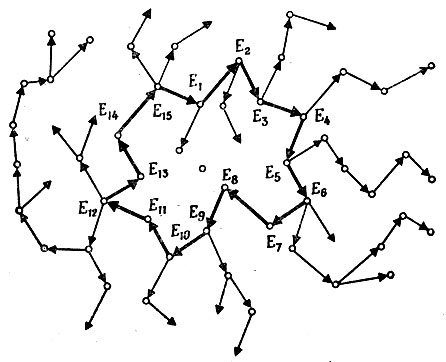
Рис. 12. Каталитическая сеть, в которой имеется замкнутая петля E₁, ..., E₁₅

Допустим теперь, что каждый катализатор в этой сети синтезируется с помощью другого катализатора. Активация данной каталитической контрольной функции происходит посредством определенных сшивок или разрывов цепей. Подобные процессы сейчас хорошо известны: например, активация, в результате которой из трипсиногена или химотрипсиногена образуется соответственно трипсин или химотрипсин, происходит путем ферментативного разрыва пептидной связи недалеко от одного конца цепи. Таким образом может возникнуть сильно разветвленная каталитическая сеть, как показано на рис. 12. Для того чтобы эта сеть стала самовоспроизводящейся, по крайней мере некоторые из этих ферментов должны быть полифункциональны (см. разветвление на рис. 12), потому что каждому ферменту для своего самовоспроизведения требуется более одного фермента. Например, если можно опознать последовательности из максимум 5 аминокислот, то для синтеза цепи с 80 пептидными связями потребуется по меньшей мере 5 ферментов, чтобы степень полимеризации увеличилась до 80, например, так:

Чем больше ферментов в этой сети, тем больше вероятность найти замкнутую петлю. Только такое замыкание кольца делает систему автокаталитической и, следовательно, гарантирует самовоспроизведение. Если петля достаточно велика, все вспомогательные функции, такие, как синтез большого числа различных олигопептидов и цепей-предшественников, могут легко локализоваться в ветвях.

V.2.2. Самовоспроизводящаяся петля и ее варианты. Сосредоточим теперь внимание на тех ферментах, которые образуют замкнутую петлю, и пронумеруем их от Е₁ до Е_n, как поступает химик-органик, когда отмечает "хромофоры" в сложной ароматической структуре. Представим эту петлю циклическим графом (рис. 13). Дифференциальные уравнения для скоростей реакций будут в общем случае нелинейны. Однако для простоты можно рассматривать линейную аппроксимацию, которая соответствует ранее разобранному случаю забуференных концентраций субстратов. Даже если это не столь реалистично, как в случае мономерных единиц - ведь субстраты для циклического пути в сети являются в основном полимерными предшественниками, - такие условия в принципе можно реализовать. Более того, основные выводы будут верны также и для нелинейного случая.

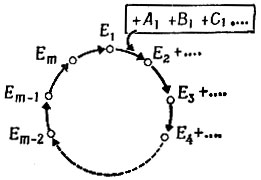
Рис. 13. Представление каталитического цикла в виде графа

Система кинетических уравнений является обобщением систем (IV.8) или (IV.18). Для каждого цикла с m членами в отсутствие ограничений отбора имеем

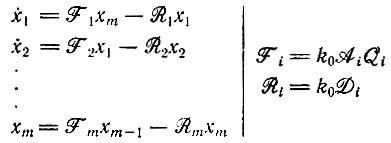(V.1)

Матрице кинетических коэффициентов

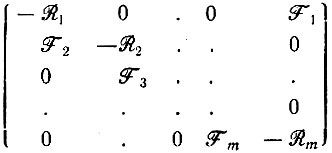(V.2)

отвечает характеристическое уравнение

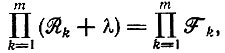(V.3)

имеющее m корней - собственных значений системы. Так как все R_i и F_i положительны, получается полином m-й степени по λ, в котором все члены, содержащие λⁱ при i ≥ 1, имеют положительные коэффициенты. Однако для постоянного члена (∼λ⁰) получается выражение

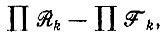(V.4)

которое отрицательно при 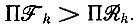В этом случае в полиноме имеется одна перемена знака, т. е. все члены, кроме последнего, положительны. Согласно правилу Декарта, здесь имеется одно положительное и (m - 1) отрицательных (возможно, комплексных) собственных значений.

По аналогии с уравнением (IV.13) при специальном условии положительное собственное значение равно

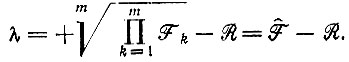(V.5)

В отсутствие распада (то есть когда все члены R равны нулю) решения сводятся просто к корням, содержащим абсолютное значение среднего геометрического 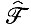умноженное на корень m-й степени из единицы, по формуле

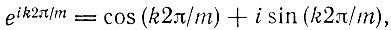(V.6)

После "уравновешивания" (т. е. после затухания m - 1 нормальных решений, соответствующих отрицательным собственным значениям) соотношение плотностей популяций различных членов цикла становится постоянным. Эти "равновесные соотношения" таковы (при условии равных R)^*:

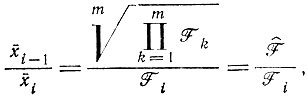(V.7)

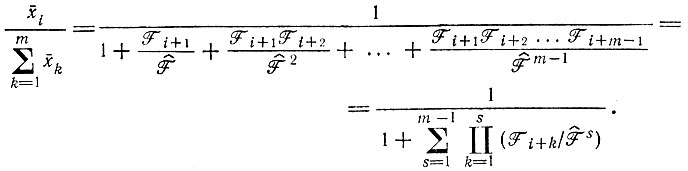(V.8)

^* (Для 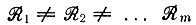соответствующие выражения гораздо более сложны, но их легко получить при помощи рекуррентных формул, начиная с тождества

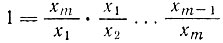
и "условия равновесия"

)

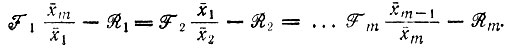
В уравнении (V.8) индексы меняются циклическим образом, т. е. i + k = i + k - m для i + k > m (k = m - i + 1, m - i + 2 ... m - 1). Физическая интерпретация полученного результата следующая: каждый цикл имеет одно нормальное решение, представляющее собой автокаталитический рост всего "коллектива", и (m - 1) нормальных решений, представляющих собой релаксационные явления, т. е. "уравновешивание" внутри цикла. Итак, замкнутая каталитическая петля эквивалентна системе с самоинструктированием или с комплементарным инструктированием.

Прежде чем перейти к анализу поведения системы, содержащей несколько конкурирующих циклов под давлением отбора, рассмотрим различные типы релаксационных сетей, чтобы получить более детальное, представление о предпосылках отбора.

Для селективного самовоспроизведения реакционной сети представляются необходимыми два условия:

1) система должна содержать "замкнутую петлю" реакций;

2) связи между реакционными состояниями должны быть каталитическими.

Чтобы иллюстрировать первое условие, можно рассмотреть общую открытую (квазилинейную) цепь реакций

+ Реагенты

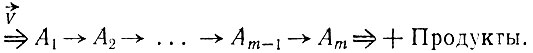(V.9)

Снова предположим, что кроме A_i, составляющих цепь, все другие реагенты имеются в больших (и, следовательно, постоянных) концентрациях, так что их можно не рассматривать явно. При постоянном реакционном потоке 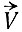различные состояния будут заполнены до стационарных уровней и вся система будет в конце концов "перетекать через край". Система будет "производить" различные состояния при благоприятных условиях, но она не будет "воспроизводить" себя, т. е. скорости продукции данных состояний не зависят от их населенности. Система - если даже некоторые или все A_i каталитически активны, т. е. участвуют в реакции не расходуясь, - не имеет важной способности к автокаталитическому росту.

Рассмотрим теперь такую же циклическую систему, как и на рис. 13, в которой, однако, не катализаторы, а простые участники и продукты реакции. Система может быть проточной, и концентрации всех участников реакции (A_i, B_i, C_i, ...), кроме E_i, снова будут постоянны. Такой цикл будет воспроизводить себя. Однако, поскольку ни один из E_i не является катализатором, система придет в стационарное состояние, где каждый из E_i после своего образования будет снова расходоваться. Несколько таких циклов не будут конкурировать друг с другом; между ними установятся стационарные отношения. Такие циклы существуют в биологических системах, и различные этапы реакции также обычно катализируются ферментами. Однако эти ферменты не воспроизводятся именно данным циклом, их производит какой-то другой "контур", который является частью самоподдерживающегося цикла живого существа в целом.

Математическое исследование позволяет получить здесь более ясную картину. В отсутствие других реакций разложения при некаталитическом превращении Е_i в Е_i+1 скорость исчезновения E_i равна скорости появления E_i+1. Таким образом, в матрице кинетических коэффициентов (V.2) все - R_i заменяются на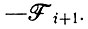

Тогда характеристическое уравнение дает только (m - 1) собственных значений, которые все отрицательны; например,

для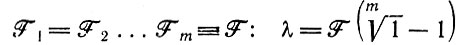

или для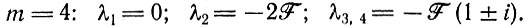

Отметим, что для нециклической реакции член в верхнем правом углу матрицы (V.2) должен отсутствовать. Для приведенного примера характеристическое уравнение сводится к 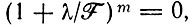что дает λ_{1, 2, 3, 4} = -F.

Для селективного самовоспроизведения существенно, чтобы участники цикла не расходовались в реакции, т. е. чтобы они были катализаторами. Однако цикл остается способным к конкуренции и самовоспроизведению, даже если не все его этапы являются каталитическими. Другими словами, не обязательно, чтобы на каждой стадии продукт реакции катализировал следующую стадию, не расходуясь при этом. Для того чтобы цикл стал автокаталитическим, достаточно, чтобы в нем производился только один такой катализатор. Это легко видеть из предыдущего рассмотрения (см. матрицу V.2). В некаталитическом цикле мы должны были бы заменить все -R_i на -F_i+1, потому что члены цикла расходуются в тех же реакциях, в которых возникают соответствующие продукты. Если, однако, первый член в цикле, и только он один, является катализатором Е₁, который образуется из Е_m, но не расходуется при образовании Е₂, то тогда верхний левый член (-R₁) в матрице (V.2) становится равным нулю.

В этом случае мы получим уравнение

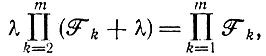(V.10)

которое имеет действительный положительный корень, например при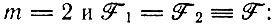

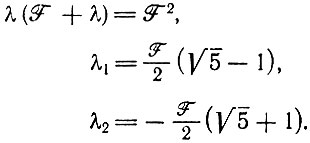(V.11)

V.2.3. Конкуренция между различными циклами: отбор. Если имеется ряд различных независимых (несвязанных) каталитических циклов, причем каждый цикл "внутренне уравновешен", то система характеризуется нормальной координатой y_i+, отвечающей положительному собственному значению. Так как в уравновешенной системе все другие нормальные решения релаксировали, мы можем заменить 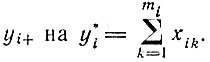Тогда уравнение отбора при постоянных силах для каждого цикла принимает общую форму

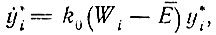(V.12)

где селективная ценность W_i определяется положительным собственным значением цикла (например, для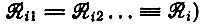

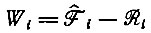(V.13)

и 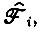согласно уравнению (V.5). Отбор может происходить только при условии, что F_i > R_i или - в случае различных 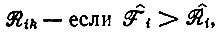где символ 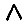означает среднее геометрическое.

По аналогии с уравнением (IV.23) мы могли бы также вычислить концентрации для отобранного цикла. Независимые циклы ведут себя как отдельные самоинструктирующиеся или комплементарные коллективы, если исходные реакции могут быть описаны системой линейных уравнений.

Циклы, однако, не обязательно должны быть независимы друг от друга. Вследствие наличия разветвлений (т. е. вследствие полифункциональности некоторых ферментов) они могут быть связаны друг с другом, как показано, например, на рис. 14. Если написать кинетические уравнения, для всех реагентов, независимо от того, к какому циклу они принадлежат, но пронумеровать их в соответствии с их принадлежностью к определенному циклу, то их свойства легко выводятся из матрицы кинетических коэффициентов (рис. 14).

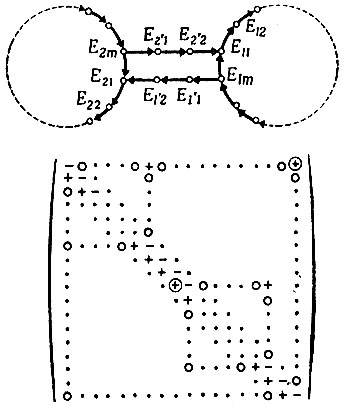
Рис. 14. Представление в виде графа циклов, связанных петлей обратной связи. Система содержит три цикла: циклы 1 и 2 плюс большая петля, включающая в себя оба эти цикла. Вследствие обратной связи циклы не конкурируют, а стабилизируют друг друга. Матрица кинетических коэффициентов всей системы описывает реакционное поведение. Столбцы соответствуют видам, а строки - реакциям. Два элемента в кружках ⊕ представляют собой точки сопряжения петель (через реакции, катализируемые E²/₂ и Е¹/₂). Если бы эти элементы обратились в нуль, то матрица распалась бы и две получившиеся при этом матрицы описывали бы два независимых (конкурирующих) цикла. Области, выделенные точками, соответствуют трем замкнутым петлям. Отрезки диагонали вне циклов 1 и 2 соответствуют ответвлениям

Типичное свойство этих систем состоит в том, что отобранный цикл (с максимальным W_i) несет с собой все связанные с ним ответвления и циклы при условии, что связь возникает в отобранном цикле. Ответвление от цикла может быть большим недостатком (если оно не несет никакой функции, полезной для воспроизведения цикла), потому что оно создает бесполезный балласт (или даже несет вредную функцию), который ограничивает возможность воспроизведения и тем самым может снизить селективную ценность W_i. Мы будем называть эти ветви "паразитными".