3.3.4. Тестирование сегрегационных отношений: редкие признаки

Основные шипы смещений. Если изучаемый признак редкий, то обычно семьи не регистрируют случайно, а начинают с "пробанда", т. е. индивида с данным признаком. Это приводит к смещениям вследствие регистрации, которые необходимо поправлять. Смещения могут быть разного рода в зависимости от способа регистрации материала.

1. Семейный или усеченный отбор. В конкретной популяции в конкретный отрезок времени учитываются все индивиды, страдающие определенным заболеванием. Пораженные регистрируются независимо друг от друга, т. е. повторный случай в сибстве малого размера будет всегда обнаружен. Усеченная регистрация возможна, например, в том случае, когда признак обязательно приводит к медицинскому обследованию, и все врачи заносят каждый случай в определенный регистр, как при проведении эпидемиологического обследования. Такая полнота сбора материала обеспечивается группой ученых, занимающихся конкретным заболеванием или группой заболеваний.

Здесь смещение вследствие регистрации обусловлено исключительно тем фактом, что регистрируются сибства, в которых уже имеется по крайней мере один пораженный. Однако, как было показано выше (разд. 3.3.3), в выборку не попадут те сибства, в которых случайно нет пораженных. Их ожидаемое количество равно

(s - количество детей в сибстве, p - сегрегационное отношение, q=1-p, n_s - число сибств размера s). Для рецессивных признаков p=0,25, но, чем меньше средний размер сибства, тем сильнее отклонение в зарегистрированных семьях от отношения 3:1.

2. Неполный множественный (пробандовый) отбор и единичный отбор как предельный случай. В большинстве исследований регистрируется не все пораженные индивиды в популяции; часто исследование начинается с когорты призывников или больных какого-либо стационара. В этом случае необходимо рассмотреть дополнительные смещения: чем больше пораженных в сибстве, тем с большей вероятностью оно попадет в выборку. Это приводит к систематическому завышению доли пораженных, которые накладываются на завышение, обусловленное усеченным отбором.

Коллер (1940) [744] привел простой пример, демонстрирующий природу такого завышения. Предположим, что пробанды регистрируются во время медицинской комиссии, которую проходит группа призывников одного года. Пусть в популяции имеется ряд семей с тремя детьми, один из которых призывного возраста и в которых хотя бы один ребенок поражен. Тогда будут зарегистрированы все семьи с тремя пораженными, две трети семей с двумя пораженными и одна треть семей с одним пораженным ребенком.

Методы коррекции, которые будут описаны ниже, могут считаться надежными, только если вероятность регистрации последующих сибсов не зависит от регистрации первого. В приведенном выше примере медицинского освидетельствования призывников это может быть и так. Однако, как правило, работа начинается с обследования стационарных больных или какой-либо другой группы лиц, подвергаемых медицинскому контролю. В этом случае в соответствии с общей практикой, если один заболевший ребенок уже прошел успешный курс лечения, то его сибс, заболевший позже, скорее попадет в ту же больницу. Однако возможна и противоположная тенденция. Беккер (1953) [564], например, собрал все случаи X-сцепленной рецессивной мышечной дистрофии Дюшенна в ограниченной области на юго-западе Германии. У него были веские основания считать, что зарегистрированы все больные. Тем не менее пораженные братья, которые заболевали не первыми в своем сибстве, как правило, учитывались не в качестве пробандов (т. е. через больницу или врача), а через первого пробанда в семье. В беседах с родителями Беккер нашел причину этой необычной ситуации. Когда заболевает первый ребенок, родители обычно обращаются к врачу. Однако затем они убеждаются в том, что исследования и терапевтические процедуры не оказывают никакого влияния на развитие заболевания, и поэтому воздерживаются от направления второго заболевшего ребенка в больницу.

3. Кроме этих смещений, которые в известной мере можно скорректировать статистическими методами, имеются и другие, которые невозможно поправить. Например, часто генетическая гипотеза формулируется на основе семейных данных, собранных из литературы. Опыт показывает, что обычно такой подход приводит к разумным результатам лишь в случае аутосомно-доминантных и X-сцепленных рецессивных заболеваний. В случае аутосомно-рецессивных болезней ситуация много сложнее: скорее появятся сообщения о семьях с существенным накоплением пораженных сибсов, чем о семьях с одним или двумя пораженными. Такой отбор по "интересным случаям" был важен в начале столетия, потому что тогда анализировали семьи с большим количеством детей. Открываемые сегодня рецессивные заболевания обычно интересны как с клинической, так и с биохимической точек зрения. Отбора такого типа можно избежать только с помощью опубликования всех случаев и путем критической интерпретации литературного материала. Но статистически правильная коррекция невозможна, поскольку в этом случае мы имеем дело с непредсказуемым систематическим смещением.

Подведем итог: методы сегрегационного анализа зависят от способа регистрации семейного материала. Отсюда следует, что способ регистрации всегда должен быть тщательно описан. Прежде всего, должны быть точно указаны все пробанды. Важно также, осознает ли автор в процессе сбора собственного материала, что он сталкивается со смещениями вследствие регистрации.

Эти рассуждения показывают, что оптимальный способ сбора материала состоит в полной (усеченной) регистрации случаев в популяции за определенный отрезок времени.

Методы коррекции смещений. Известны два разных типа таких методов: связанные с тестированием или с оценкой.

В методах тестирования наблюдаемые значения сравниваются с ожидаемыми, уже поправленными с учетом смещения вследствие регистрации. Впервые такой метод был предложен Бернштейном (1929) [744] для усеченного отбора. Ожидаемое число пораженных E_r равно

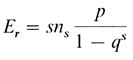
в сибствах размера s (обозначения те же, что и для формулы 3.2). Аналогичный метод применим и для отбора по пробандам.

Методы тестирования отвечают на очень конкретный вопрос: "Согласуются ли наблюдаемые пропорции с ожидаемыми в соответствии с определенной генетической гипотезой?"

Во многих, если не во всех, реальных случаях вопрос ставится шире: "Каково несмещенное сегрегационное отношение в наблюдаемых сибствах?" Это проблема оценки. Самый первый метод был опубликован Вайнбергом (1912) [936] и назван сибсовым методом. Начиная с каждого пораженного сибса, определяется число пораженных и непораженных среди сибсов. Этот метод соответствует "усеченному отбору", т. е. когда каждый пораженный в то же время является пробандом. Сибсовый метод-это предельный случай "пробандового метода", который используют, когда семьи зарегистрированы с помощью неполного множественного отбора по пробандам. Число пораженных и непораженных сибсов подсчитывают, начиная с каждого пробанда. Предельным случаем, но уже с "другой стороны", служит единичный отбор. Здесь в каждом сибстве только один пробанд, и подсчет осуществляется один раз среди его сибсов.

При увеличении размера выборки оценки сходятся к параметру р, истинному сегрегационному отношению, т. е. эти оценки состоятельны. Однако уже давно стало очевидно, что они не эффективны, за исключением предельного случая единичного отбора, т. е. не используют оптимальным образом всю имеющуюся информацию. В связи с этим ряд авторов попытались улучшить свойства оценок. Здесь мы опишем метод взвешенных оценок, предложенный Финнеем [663], в модификации Кэлина (1953) [729]. Для его реализации достаточно калькулятора. Детальное описание метода оценки будет дано в приложении 3 для двух крайних вариантов: усеченный отбор (k=1) и единичный отбор (k=0), где k - вероятность регистрации семьи. При k=1 получается наибольшая оценка p̂ сегрегационного отношения p, а при k=0 - наименьшая. Кроме того, в приложении 3 будут обсуждаться другие статистические проблемы генетического анализа, такие, как генетическая гетерогенность, примесь спорадических случаев, тестирование эффекта порядка рождения. Различные методы применяются для сбора семей с глухонемотой. Более сложные проблемы возникают при изучении сегрегации при хромосомных транслокациях, поскольку в этом случае семьи могут быть зарегистрированы через пробандов - носителей как несбалансированных, так и сбалансированных транслокаций, а также при популяционном исследовании (см. разд. 2.2.2). Соответствующие методы анализа будут обсуждаться в приложении 3.