
3.6. Условия и ограничения генетического анализа у человека: мультифакториальное наследование
3.6.1. Уровни генетического анализа
Теория наследственности, созданная Менделем на основании опытов по скрещиванию гороха (разд. 1.4), претерпела в своем развитии несколько этапов. По современным представлениям ген-это фрагмент двухцепочечной ДНК, несущий определенную генетическую информацию. В первых разделах книги мы рассматривали признаки, на примере которых можно было бы ознакомиться с фундаментальными принципами и четко продемонстрировать взаимодействие генотипа и фенотипа: для "нормальных" признаков - это группы крови, а для "аномальных" - редкие наследственные заболевания.
Существует, однако, много таких нормальных признаков, генетическая изменчивость которых очевидна, но ее трудно объяснить простым типом наследования. К этим признакам относят, например, рост и пропорции тела, черты и выражение лица ("этот ребенок - вылитый отец"), цвет кожи, кровяное давление и другие. Многие заболевания могут вызываться целым комплексом разных причин, но подверженность патологии может быть различной для разных индивидов и детерминироваться генетически. На ранних этапах развития генетики эти эмпирические данные часто наивно пытались согласовать с менделевскими правилами, не заботясь о том, соблюдены ли формальные требования, связанные с простыми типами наследования. Теперь существует другая тенденция описывать изменчивость таких признаков на основе слишком упрощающих биометрических моделей. Полученные при этом выводы настолько сильно зависят от исходных предположений, что их биологическое значение остается часто сомнительным. Вот почему мы считаем полезным изложить логические основы обсуждения генетических гипотез и очертить несколько уровней, где генетический анализ в настоящее время возможен.
3.6.1.1. Генный уровень
Конечная цель генетического анализа - выявить различия на уровне ДНК, т. е. идентифицировать мутантный сайт. Последовательность нуклеотидов в ДНК содержит информацию для последовательности аминокислот в полипептидной цепи. Вот почему, если прямой анализ на уровне ДНК невозможен, определяют различия на уровне аминокислотной последовательности белков, а по ней уже судят о перестройке на уровне ДНК. Впервые это было осуществлено для гемоглобинов (разд. 4.3). Впоследствии такой анализ позволил сделать вывод о перестройках в ДНК, кодирующих другие белки. Оказалось, что у большинства мутантных белков в определенном положении одна аминокислота замещена на другую в результате замены нуклеотида в соответствующем кодоне. Обнаружены и другие перестройки: делеции, сдвиг рамки считывания и нонсенс-мутации (разд. 4.3, 5.1). В этом случае генетический вариант белка является непосредственным результатом специфического изменения на уровне ДНК - "носителя генетической информации".
Разработанные в последние годы методы позволяют иногда прямо продемонстрировать мутационную перестройку на уровне ДНК (разд. 4.3.5). Все расширяющиеся возможности таких методов позволяют открывать новые типы мутаций, в частности вызывающие нарушения регуляции транскрипции, а также ошибочный сплайсинг первичных транскриптов. Большинство исследований этого типа было выполнено с системой β-глобина человека, мутационные изменения которого проявляются фенотипически в виде группы заболеваний, называемых β-талассемиями. Последние возникают вследствие или отсутствия (β0), или недостаточности продукции β-цепи (β+). По мере того как количество ДНК-зондов для разных генов человека растет, все большее число мутаций становятся доступными для анализа на уровне ДНК. Мы уже знаем, что различные мутации, аналогичные найденным при гемоглобинопатиях, обнаружены при гемофилии и семейной гиперхолестеринемии. Можно ожидать, что в будущем природу мутационных изменений у человека будут изучать именно на уровне ДНК, а не на уровне генных продуктов.
3.6.1.2. Анализ продукта гена: биохимический уровень
В этом случае идентифицировать мутантный сайт внутри гена невозможно, можно только идентифицировать ген, в котором произошла мутация. Для этого существует несколько способов.
- Специфические белки можно охарактеризовать биохимически. Обнаруженные различия отражают генетическую изменчивость. Если белок состоит из нескольких полипептидных цепей, можно идентифицировать мутантный полипептид.
- Многие белки выполняют функции ферментов, катализирующих специфические метаболические реакции. Следовательно, если продемонстрирован конкретный генетический блок, определен дефект фермента и исключены все другие биохимические объяснения, можно сделать вывод о мутации в конкретном гене, кодирующем данный фермент. Следующий шаг будет состоять в детальном изучении фермента.
- Идентифицировать мутантный ген можно и на основании анализа антигенного профиля клеточной поверхности. Примерами служат группы крови и система HLA (разд. 3.5.5). В этих случаях удается выявить не только конкретные гены, но иногда также и структурные различия внутри отдельных генов.
Результаты анализа на биохимическом уровне у человека сопоставимы с результатами, полученными в экспериментальной генетике таких видов, как Drosophila melanogaster, мышь, кукуруза, шелковичный червь и другие. У этих видов во многих случаях мутации идентифицировали не на основе изменений специфических белков, ферментативных дефектов или аберрантных антигенов, а благодаря опытам по скрещиванию и рекомбинационному анализу, что в совокупности обеспечивает эффективный альтернативный подход к идентификации индивидуальных генов.
Интересно проследить, как чисто формальная концепция гена, долгое время господствовавшая в умах экспериментальных генетиков, влияла на развитие этой фундаментальной науки. Отметим, что на ранних этапах биохимическая генетика человека развивалась более успешно, нежели на других видах. Сочетание биохимического и генетического подходов к генетике бактерий и грибов привело к значительным успехам. Однако в сравнении с другими видами млекопитающих биохимическая генетика человека продолжает оставаться впереди. С появлением новых молекулярных методов генетический анализ у человека значительно упрощается.
3.6.1.3. Качественный феногенетический анализ: простые типы наследования
В данном случае выводы основаны на анализе фенотипических различий, отдаленных от первичного действия генов. Тем не менее иногда соответствие генотипа и фенотипа столь однозначно, что напрашивается вывод о простом менделевском наследовании. Однако мы не можем с уверенностью утверждать, что этот ген единственный, поскольку один и тот же фенотип даже с одинаковым типом наследования может быть обусловлен мутациями в нескольких разных локусах.
Редко встречающиеся качественные отклонения от нормы. Эта категория охватывает большинство наследственных заболеваний. Например, индивид либо имеет нормальную пигментацию, либо утратил кожный пигмент (альбинизм). Если выражение признака можно оценить количественно, например измерить уровень метаболитов крови или мочи, то распределение фенотипических значений имеет две моды. Результаты подобного рода позволяют заподозрить наличие ферментативного дефекта и, возможно, даже идентифицировать соответствующий ген. Примерами могут служить повышенное выделение гомогентизиновой кислоты в моче больных алкаптонурией (врожденная ошибка метаболизма по Гэрроду) или повышенное содержание фенилаланина в сыворотке крови больных фенилкетонурией (рис. 3.46). Эти признаки редкие, и когда их подвергают детальному анализу, клинически сходные заболевания с одинаковым типом наследования часто оказываются генетически гетерогенными. Каковы критерии гетерогенности?
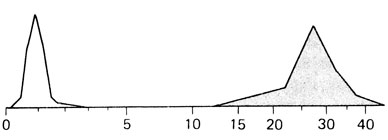
Рис. 3.46. Уровень фенилаланина в плазме крови здоровых людей и больных фенилкетонурией (окрашено), выраженный в мг%. (По Penrose, 1951.)
- Если ребенок двух гомозигот с рецессивным признаком имеет нормальный фенотип, это означает, что его родители гомозиготны по разным рецессивным генам.
- При анализе родословных в одних семьях обнаруживается тесное сцепление заболевания с геном-маркером, тогда как в других семьях эти гены сегрегируют независимо. Примером может служить сцепление одного из локусов доминантного эллиптоцитоза с геном Rh в хромосоме 1.
- В ряде клинически сходных случаев биохимический анализ выявляет дефекты различных белков (или ферментов). Оказалось, что признаки, которые сначала считались однородными, имеют разную генетическую основу (примеры: гемофилия А и В, болезни накопления гликогена, наследственные гемолитические анемии.)
Широко распространенные признаки: бимодальное распределение. Для этой группы признаков характерно отсутствие четкого распределения фенотипов по двум классам: не каждого индивида можно с уверенностью отнести к какому-то определенному классу, поскольку возможны перекрывания. Но если область перекрывания фенотипических значений относительно небольшая, то общее распределение остается все же бимодальным.
Это явление можно проиллюстрировать примером из фармакогенетики. После приема одинаковой дозы противотуберкулезного препарата - гидразида изоникотиновой кислоты (INH) его концентрация в плазме разных индивидов оказывается различной, а общее распределение имеет две моды (рис. 3.47). Можно предположить, что механизм биотрансформации лекарства детерминирован одним геном. Эта гипотеза была подтверждена в семейных исследованиях: у гомозигот Acs/Acs (Acs - аллель медленной инактивации) обнаружился высокий уровень лекарства в крови, тогда как у гетерозигот Acs/Acr (Acr - аллель быстрой инактивации) и у гомозигот Acr/Acr выявлялся низкий уровень лекарства. Был сделан вывод о том, что эти фенотипические различия в биотрансформации обусловлены наследуемыми вариантами фермента N-ацетилтрансферазы. Таким образом, подтверждение генетической гипотезы было получено благодаря открытию бимодального распределения концентраций лекарств в крови.
![Рис. 3.47. Концентрация изониазида (INH) в плазме крови 267 членов 53 семей. Антимода полученного бимодального распределения соответствует области между 2 и 3 мг% [196]](pic/000222.jpg)
Рис. 3.47. Концентрация изониазида (INH) в плазме крови 267 членов 53 семей. Антимода полученного бимодального распределения соответствует области между 2 и 3 мг% [196]
Если исследуемый признак допускает измерение и обнаруживает бимодальное распределение, это еще не может служить доказательством простого типа наследования. Нужны более убедительные факты, поскольку возможны и другие причины бимодальности.
- Бимодальное (или мультимодальное) распределение особенно вероятно при наличии так называемого порогового эффекта (разд. 3.6.2). Кроме того, даже в отсутствие порогового эффекта бимодальное распределение может возникать вторично, если признак обнаруживает тенденцию к "самоусилению" при достижении определенной степени выражения. Одним из примеров может служить кровяное давление: при определенном повышении его уровня почки могут уже не справляться со своими функциями, что влечет за собой более резкое повышение кровяного давления. Бимодальность может имитироваться также особенностями регистрации семейного материала.
- Средние значения двух распределений могут быть столь близкими друг к другу, что бимодальность окажется незаметной. Харрис и Смит [703] исследовали условия, при которых комбинация двух нормальных распределений может привести к бимодальному распределению:
а) два нормальных распределения с одинаковыми дисперсиями дают в совокупности бимодальное распределение, только если разность средних значений по крайней мере в два раза больше общего стандартного отклонения;
б) в случае различных дисперсий, если разность между средними значениями выражать в единицах меньшего стандартного отклонения, то коэффициент должен изменяться от 2 (когда дисперсии равны) до 2,6 (когда дисперсии сильно различаются);
в) если средние значения настолько близки между собой, что бимодальность общего распределения не выявляется, а численности индивидов в двух распределениях различаются не много, то на наличие двух разных распределений может указывать так называемая "битангенциальность" общего распределения (рис. 3.48).
![Рис. 3.48. Битангенциальное распределение. (Harris, Smith, 1951 [703].)](pic/000223.jpg)
Рис. 3.48. Битангенциальное распределение. (Harris, Smith, 1951 [703].)
На практике трудно убедиться в наличии именно такого распределения. Встречающиеся в природе переменные редко имеют идеальное нормальное распределение, и поэтому следует помнить о случайных выборочных отклонениях. Убедиться в том, что случайные отклонения иногда искажают распределение эмпирически наблюдаемых значений при умеренном объеме выборки, можно при сравнении рис. 3.48 с рис. 3.47.
Вывод. Унимодальное распределение может свидетельствовать о моногенном наследовании, однако в отсутствие дополнительных данных отличить моногенную модель от мультифакториальной невозможно.
На рис. 3.49 представлен противоположный пример: распределения ферментативной активности разных электрофоретически идентифицируемых генетических вариантов GPT (глутамат-пируват-трансаминазы) четко различаются. При этом общее распределение в популяции является почти нормальным, что принято интерпретировать как отражение мультифакториальной природы признака. Тем не менее в данном случае общее распределение в популяции детерминировано лишь двумя аллелями (GPT1, GPT2) и соответственно тремя фенотипами (GPT1, GPT2-1, GPT2). Много случаев такого рода было обнаружено при анализе изменчивости ферментативной активности в различных системах генетически полиморфных ферментов (разд. 6.1).
![Рис. 3.49. Распределения ферментативной активности для трех генотипов GPT и их суммарное распределение, очень сходное со скошенным нормальным [8]](pic/000224.jpg)
Рис. 3.49. Распределения ферментативной активности для трех генотипов GPT и их суммарное распределение, очень сходное со скошенным нормальным [8]
Распознавание бимодальности может быть существенно затруднено, если два класса имеют очень разные частоты, например если численность индивидов одного класса составляет менее 10% от численности другого (рис. 3.50). В этой ситуации возникает сомнение, является ли меньшая мода истинной, отражающей наличие генетически особой группы. И в таких случаях также возможны:
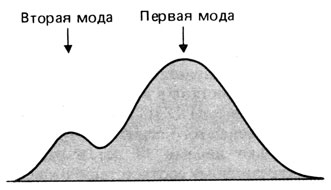
Рис. 3.50. Бимодальное распределение количественного признака в популяции человека. Один из двух типов распространен намного чаще, чем другой
а) случайные отклонения;
б) пороговый эффект: к этой возможности следует отнестись серьезно, особенно если фенотипические значения, образующие вторую моду, близки к нулевым.
Влияние случайных отклонений можно избежать, если исследовать большее количество индивидов, но при этом не исключается, конечно, пороговый эффект. Необходимы семейные исследования, особенно в случаях аутосомно-рецессивного или сцепленного с полом наследования. В таких семьях следует ожидать наличия двух генотипов примерно с равными частотами, и поэтому бимодальность будет выражена более четко, чем в популяционной выборке. При исследовании семей пробандов, фенотипы которых соответствуют меньшей моде, в пользу простого типа наследования свидетельствуют следующие факты (если они типичны для большинства семей):
а) четко выраженное бимодальное распределение признака в сибствах, причем значения фенотипических признаков у сибсов, соответствующие моде "нормы", имеют распределение такое же, как и в общей популяции;
б) значения у родителей также образуют бимодальное распределение с тем дополнительным условием, что по крайней мере один из родителей должен попасть в группу второй моды, отличной от "нормы";
в) в этих сибствах соотношение пораженных и непораженных должно быть примерно 1:1. Если оба родителя попадают во вторую моду, т. е. оба гетерозиготны, то соотношение пораженных и непораженных сибсов должно быть примерно 3:1.
При мультифакториальном наследовании ложная бимодальность может оказаться следствием порога в области нулевых значений. В результате распределение тех сибсов, фенотипические значения признака которых, можно отнести к первой моде, будет обнаруживать меньшее среднее значение, чем в популяции. Кроме того, значения признака у родителей чаще будут относиться к первой моде с более низким средним значением, чем в популяции (рис. 3.51).
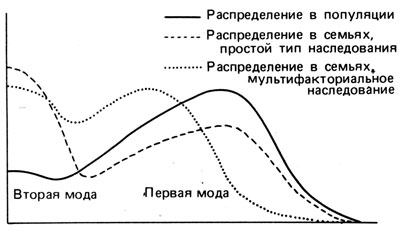
Рис. 3.51. Бимодальное распределение в случае, когда вторая мода близка к нулю. Различие между простым диаллельным наследованием и мультифакториальной моделью. Отметим, что при мультифакториальном наследовании первая мода сдвинута влево, тогда как при диаллельном наследовании первая мода совпадает с популяционной модой и модой в тех семьях, в которых происходит расщепление на два типа
Признак, для которого вывод об аутосомно-доминантном наследовании был сделан на основе указанных критериев, - это низкая амплитуда электроэнцефалограммы (ЭЭГ) [921]. Человеческий мозг постоянно порождает электрические колебания, которые после прохождения через соответствующие усилители можно записать в виде кривых на бумаге. Для этого к голове в определенных точках прикладывается несколько (8-16) электродов. Испытуемый расслабляется и отдыхает, но не спит (типы ЭЭГ сна различны и сами по себе часто используются в специальных диагностических целях). В ЭЭГ отдыхающего здорового взрослого человека обнаруживается несколько разных типов волн, среди которых наиболее примечательны α-волны, характеризующиеся умеренной частотой колебаний. Кроме этого могут присутствовать быстрые β-волны (с частотой более 13 колебаний в секунду) и несколько видов медленных θ-волн (4-8 колебаний в с) (рис. 3.52). Комбинации различных элементов кривой ЭЭГ многообразны, их можно сравнивать между собой. Почти каждый человек имеет свою собственную, характерную только для него ЭЭГ, которая остается постоянной многие годы в отсутствие таких заболеваний, как эпилепсия или опухоль мозга, а также исключая такие кратковременные физиологические состояния, как сильное утомление или тяжелая интоксикация. В детстве и юности ЭЭГ развивается из нерегулярных форм с относительно медленными волнами, завершает свое развитие примерно к 19 годам, а затем меняется очень мало. Индивидуальные различия в скорости развития огромны, что объясняет высокую изменчивость ЭЭГ в детском возрасте. Близнецовые исследования показали, что в норме индивидуальные различия ЭЭГ детерминированы почти исключительно генетически.
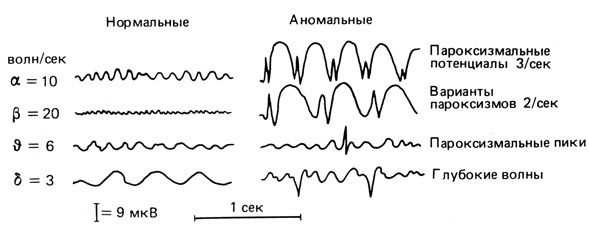
Рис. 3.52. Типы колебаний (волн) электроэнцефалограммы человека
Примерно у 4% взрослых индивидов из общей популяции обнаружены ЭЭГ со следующими характеристиками:
а) α-волны затылочной области полностью отсутствуют или выявляются только короткое время с очень низкой амплитудой;
б) ЭЭГ может выглядеть абсолютно плоской или обнаруживать нерегулярную картину с β- или θ-волнами низкой амплитуды;
в) в противоположность ЭЭГ с нормальным α-ритмом отсутствует реакция на открывание глаз. После закрывания глаз могут появиться, но не обязательно, отдельные α-волны.
Первым требованием генетического анализа является, конечно, возможность количественно оценить α-ритм в затылочной области. Одной из мер может служить так называемый α-индекс, определяемый следующим образом:
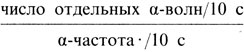
На рис. 3.53 показано распределение этого индекса в 30 сибствах, зарегистрированных по пробандам с низкой амплитудой ЭЭГ. Это распределение имеет два максимума, один около 70-80, а другой около 0. Второй максимум соответствует низкой амплитуде. На первый взгляд это распределение свидетельствует в пользу моногенной гипотезы, однако второй максимум близок к нулевому значению и, следовательно, бимодальность распределения может оказаться следствием порога, расположенного в нулевой точке, т. е. фиктивной.
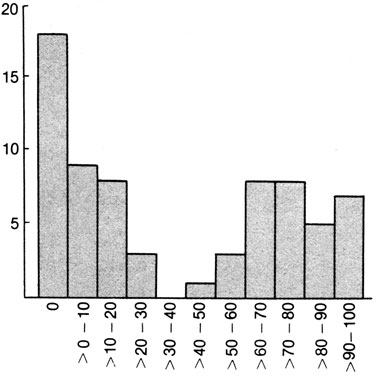
Рис. 3.53. Распределение α-индекса в 30 сибствах из семей пробандов с низкоамплитудными ЭЭГ (см. текст)
Имеются ли дополнительные аргументы в пользу моногенного наследования? Распределение среди родителей является бимодальным, а распределение вокруг первой моды хорошо согласуется с распределением в общей популяции. Еще важнее то, что во всех семьях, зарегистрированных по пробанду, по крайней мере один родитель имел низкую амплитуду ЭЭГ (рис. 3.54). Сегрегационный анализ данных по всем семьям с двумя пораженными родителями дал оценку вероятности расщепления, близкую к 75%, но по всем семьям с одним пораженным родителем оценка этой вероятности была значительно ниже ожидаемого значения, равного 50%. Оказалось, что такой результат - следствие включения в выборку подростков в возрасте от 10 до 19 лет: низкая амплитуда ЭЭГ как раз только формируется в течение этого периода. Ограничение анализа только лицами 19 лет и старше приводит к превосходному соответствию ожидаемых и наблюдаемых сегрегационных отношений (табл. 3.12). (Ожидаемые значения иногда выше, чем 0,5 или 0,75 соответственно, поскольку вследствие высокой частоты признака среди родителей ожидается некоторая доля гомозигот.) В описанном случае анализ распределений количественного признака (α-индекс) в семьях позволил сделать вывод об аутосомно-доминантном типе наследования.
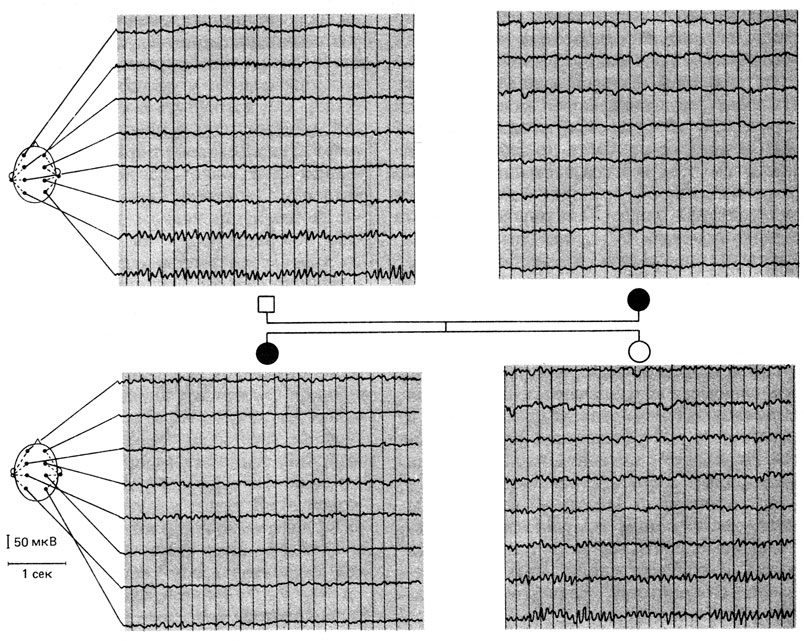
Рис. 3.54. Семейное обследование. У матери и первой дочери низкоамплитудные ЭЭГ, у отца и второй дочери стандартная ЭЭГ с α-ритмом. Униполярные отведения
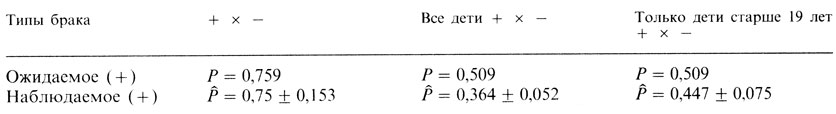
Таблица 3.12. Низкоамплитудная ЭЭГ (+): сегрегационный анализ 60 семей со 117 детьми
P - ожидаемое; P̂ - оцененное сегрегационное отношение. Ожидаемые значения были вычислены в предположении, что подавляющее большинство родителей с низкоамплитудной ЭЭГ (+) были гетерозиготами (ожидаемые значения для детей в скрещиваниях + × +: 0,75; + × -: P=0,05), а родители, для которых вычисления проводились в предположении равновесия Харди - Вайнберга, были гомозиготами.
В принципе сходные критерии можно использовать при изучении X-сцепленного рецессивного наследования. Однако в этом случае анализ распределений может оказаться труднее для женской части популяции, поскольку ожидается тримодальное распределение: две гомозиготы и одна гетерозигота. Примером может служить активность глюкозо-6-фосфатдегидрогеназы (G6PD): так как существуют большие перекрывания между "нормой" и гетерозиготами, а также между гетерозиготами и гомозиготами по недостаточности G6PD, в женской части популяции трудно идентифицировать тримодальность.
3.6.1.4. Генетический анализ на уровне количественного фенотипа - биометрический уровень
Аддитивная модель. Во многих случаях фенотипическая изменчивость настолько сложна, что эффекты отдельных мутаций уже нельзя идентифицировать и приходится мириться с генетическими выводами (основанными на анализе сходства между родственниками), представленными в очень общем виде. Тем не менее применяемые в этих случаях "мультифакториальные" модели имеют вполне определенные характеристики, и что важнее, формулируемые на их основе прогнозы оказываются справедливыми при тестировании на реальном материале.
В простейшей из возможных моделей предполагается совместное действие нескольких генов. Предположим, что аллель, обозначаемый заглавной буквой (A или B, но не a или b), вносит свой вклад в величину признака ("положительный" аллель), тогда как аллель, обозначаемый маленькой буквой (a или b, но не A или B), действует как "нулевой", т. е. не оказывает никакого эффекта на величину признака ("отрицательный" аллель). Тогда фенотипическое проявление признака будет находиться в градуальной зависимости только от относительного количества положительных (или отрицательных) аллелей, вклады которых предполагаются в этой модели равными и аддитивными. Таким образом, генотипы AABBccdd..., AaBbCcDd или aabbCCDD... фенотипически не различаются (аддитивная полигения). Эту модель мы используем в дальнейшем для разъяснения ряда концепций. Необходимо пояснить, что эта модель представляет собой абстракцию и является очень упрощенной. На самом деле вклады генов, действующих в мультифакториальной системе, почти всегда будут различаться как в количественном, так и в качественном отношении. Какие-то гены окажутся более важными.
Давайте далее предположим, что рассматриваемые n диаллельных генов распространены в популяции с частотами p (для положительных аллелей) = q (для отрицательных аллелей) = 0,5. Тогда распределение фенотипических классов на произвольной количественной шкале задается биномиальной формулой (p+q)2n (рис. 3.55). Чем больше число генов, тем больше индивидов находится в центральной (т. е. ближе к средним значениям) области распределения. На первый взгляд эта зависимость может дать критерий оценки количества генов, детерминирующих признак (для чего следует сравнить эмпирическое распределение с некоторым набором теоретических). Однако такое предположение будет справедливым лишь в том случае, если каждый ген вносит в величину признака на периферии распределения точно такой же вклад, как и в центре. Это предположение можно оспорить на основе общей и часто биологически приемлемой гипотезы, согласно которой на периферии распределения дальнейшие отклонения в том же направлении достигаются труднее. Например, в случае биологически активных веществ и ферментов отрицательные значения активности не существуют.
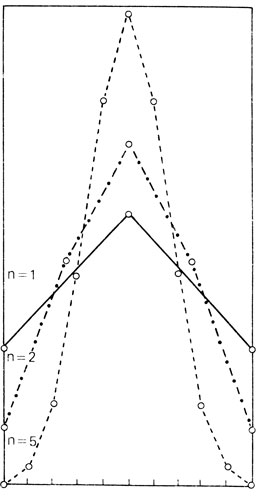
Рис. 3.55. Распределение генотипов в соответствии с биномиальным распределением (p+q)2n при p=q=0,5 для 1, 2, 5 пар генов (n = 1, 2, 5). Ось абсцисс соответствует значениям измеряемого признака
Подобные рассуждения использовали для определения числа генов, детерминирующих пигментацию кожи. По нашему мнению, весьма вероятно, что число таких генов не очень велико, поскольку среди детей в браках между мулатами (т. е. множественными гетерозиготами) нередко наблюдается выщепление как чисто "белых", так и чисто "черных" индивидов.
Все распределения на рис. 3.55 имеют только одну моду (т. е. они унимодальны). Кроме того, они сходны с "нормальным" распределением. Это сходство увеличивается с возрастанием числа рассматриваемых генов (n), т. е. при возрастании n нормальное распределение является предельным случаем биномиального. Можно показать, что эта аппроксимация становится удовлетворительной как раз тогда, когда частоты положительных и отрицательных аллелей не равны. Чем ближе к симметрии, тем большие значения n требуются для достижения той же степени аппроксимации. Вообще, унимодальное распределение, которое более или менее точно аппроксимируется нормальным, является типичным для генетической модели аддитивной полигении. Однако ни унимодальность распределения, ни его форма не зависят от конкретных свойств этой модели (равных и аддитивных вкладов генов) и потому могут служить индикаторами мультифакториального наследования в более общем смысле.
С другой стороны, как показано в разд. 3.6.1.3, эти свойства не исключают наличия эффекта "главного гена" с простым типом наследования, который действует на фоне аддитивно-полигенной системы. Биологически вполне правдоподобно, что лишь несколько главных генов могут быть основными генетическими факторами ряда заболеваний, проявляющими свои эффекты на фоне многих генов, менее значимых для патогенеза этих заболеваний.
Самое первое условие установления унимодальности распределения, как и его близости к нормальному, - возможность измерить признак на какой-либо количественной шкале. Например, всех взрослых мужчин можно разбить по росту на два альтернативных класса: на тех, которые выше 167 см, и на тех, которые ниже 167 см. При такой ограниченной информации нетрудно показать на основе семейных данных, что изменчивость роста человека зависит от доминантного гена с неполной пенетрантностью. Этот пример тривиален, и аргументация очевидна, однако литература все еще полна примеров такого типа ошибок. Генетическая гипотеза не может основываться исключительно на популяционном распределении признака. Необходимы также семейные данные. Какого типа семейные данные предсказывает модель? Мы рассмотрим этот вопрос в простейшем случае двух генов с двумя аллелями каждый (A, a и B, b), действующими аддитивно и одинаково. Пусть частоты аллелей равны p1, p2 и q1, q2 соответственно. Тогда мы будем иметь девять разных генотипов и пять разных фенотипов. Их частоты приведены в табл. 3.13. Можно вычислить частоты возможных типов браков и распределение генотипов детей для каждого типа брака родителей. Для частного случая, когда частоты всех аллелей равны 0,5 (последний столбец в табл. 3.13), вычисления приведены в табл. 3.14. Из этих распределений генотипов можно получить соответствующие фенотипические распределения детей (табл. 3.15).
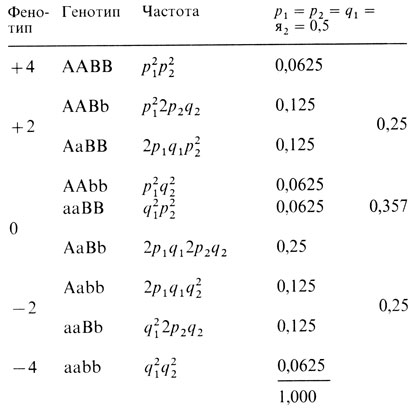
Таблица 3.13. Генотипы и фенотипы при аддитивном полигенном наследовании
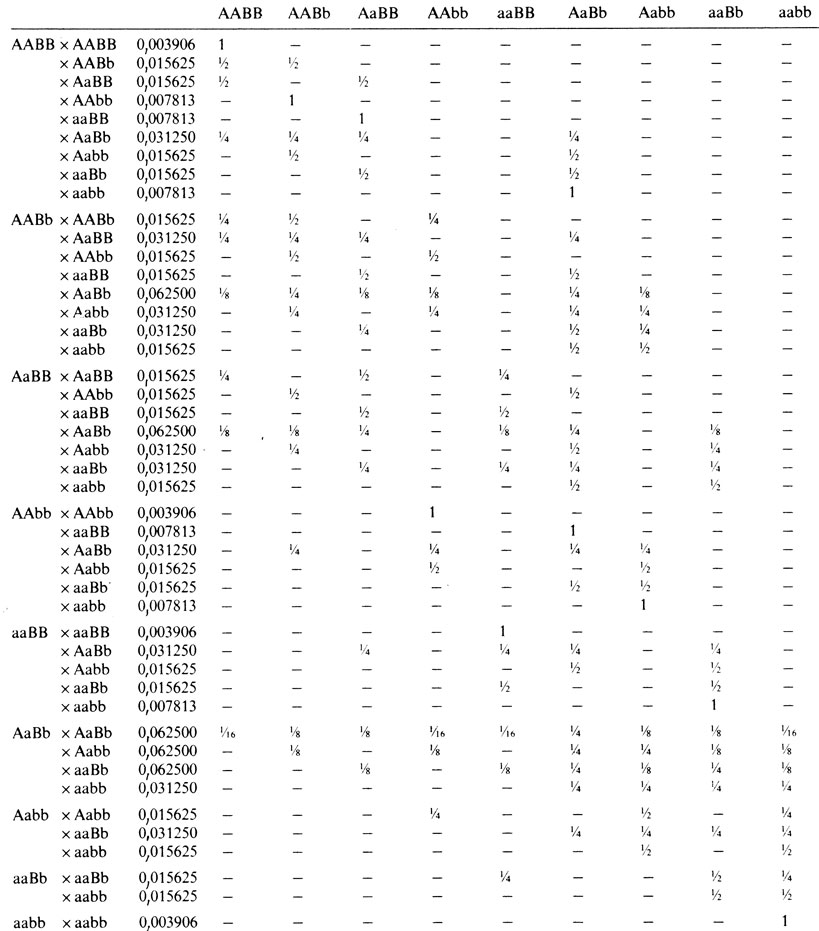
Таблица 3.14. Типы браков, их частоты и сегрегационное отношение среди детей в случае двух генов (p1=p2=q1=q2=0,5)
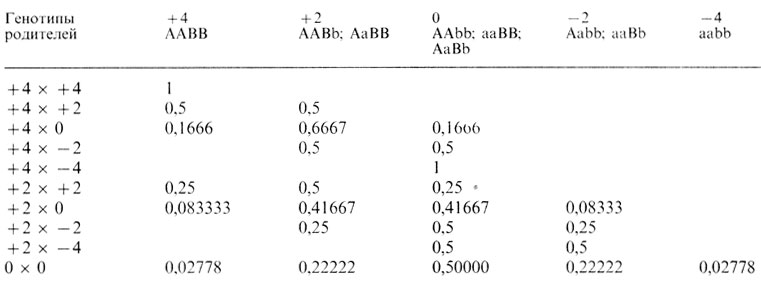
Таблица 3.15. Распределение детей при аддитивном полигенном наследовании (не приведены пять классов 0×-2, 0×-4, -2×-2, -2× 4, -4×-4, расчеты для которых могут быть проведены по тому же правилу)
Изучаемая модель обладает следующими свойствами:
а) все получающиеся распределения имеют примерно одинаковую форму: они симметричны и унимодальны;
б) если родительские фенотипы совпадают, то средняя детей равна родительскому фенотипу. Если родительские фенотипы различны, то средняя детей точно равна среднему родительских значений (значение среднего родителя);
в) с увеличением гетерозиготности родителей ожидаемая дисперсия детей становится больше. Она наибольшая для брака 0×0 и равна 0 для браков +4×4; +4×-4; -4×-4;
д) средняя детей всех лиц с одинаковым генотипом (например, дети всех лиц с фенотипом +4) отклоняется вдвое меньше от популяционной средней, чем фенотип этих родителей (например, для родителей с фенотипом +4 фенотипическая средняя детей равна +2).
Эта модель очень частная и простая. Но даже ее анализ оказывается уже крайне громоздким. Для изучения общего случая (n генов, частоты аллелей p1,...,pn; q1,... qn) метод необходимо видоизменить. Сначала предположим, что пара аллелей гетерозигот Aa имеет фенотипический эффект α, гомозигот AA-2α, а гомозигот aa-0. Таким образом, мы снова предположили, что гетерозиготы занимают промежуточное положение между гомозиготами. Среднее значение и дисперсию признака x можно вычислить следующим образом:
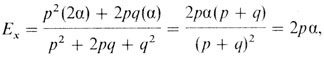
(3.5)
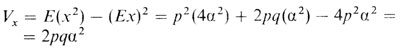
(3.6)
(здесь p+q=1). α может рассматриваться как вклад аллеля A в признак x. Vx называется генетической изменчивостью в популяции.
В общем случае n генов с частотами pi=p1, p2, ..., pn для аллелей A1, A2, ..., An и частотами qi=q1, q2, ..., qn для аллелей a1, a2, ..., an
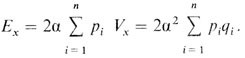
Наши рассуждения, которые для простоты ограничены случаем одного гена, справедливы и в общем случае n генов.
Рассмотрим теперь соотношения между родителями и детьми, а также между сибсами. Для упрощения вычислений предположим, что а равна 1, тогда фенотипическое значение гомозигот AA=2, гетерозигот Aa=1 и гомозигот aa=0. В табл. 3.16 показаны частоты всех возможных комбинаций мать - ребенок. Их можно объяснить следующим образом. Частота матерей AA среди всех матерей равна p2. Каждый из их детей получает один аллель A. Вероятность, что этот аллель встретит в зиготе другой аллель А, равна р. Это дает общую частоту p2·p=p3. Для других материнских генотипов можно провести аналогичные расчеты. Общее распределение для всей популяции (родителей и детей) будет, конечно, p2+2pq+q2 (маргинальные суммы в табл. 3.16).

Таблица 3.16. Частоты пар родитель - ребенок (комбинации отец-ребенок или мать-ребенок) в популяции человека при случайном скрещивании (см. текст)
Обозначим теперь изучаемый признак у родителей x1, а у детей x2. Тогда полученные выше уравнения (3.5) и (3.6) дадут
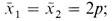
(3.7)
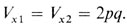
(3.8)
Ковариацию между родителями и детьми можно получить из табл. 3.17. В общем случае ковариация двух переменных x1 и x2 определяется так:
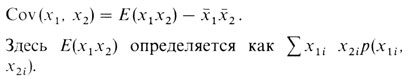
![Таблица 3.17. Рост родителей и взрослых детей. (По Johannsen, 1926 [726].) (Данные приведены в дюймах: 1 дюйм = 2,54 см.)](pic/000245.jpg)
Таблица 3.17. Рост родителей и взрослых детей. (По Johannsen, 1926 [726].) (Данные приведены в дюймах: 1 дюйм = 2,54 см.)
Значения x1i и x2i представляют собой фенотипическое выражение признака, т. е. в нашем примере, 2,1,0. p(x1i, x2i) - соответствующие записи в табл. 3.16, например, p(2,2) имеет значение q3. Отсюда следует
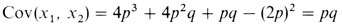
и коэффициент корреляции между родителем и ребенком
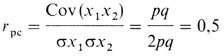
Этот важный результат был получен Фишером (1918) [664]. В случайно скрещивающейся популяции и при аддитивном действии генов коэффициент корреляции между родителем и ребенком составляет 0,5. Точно таким же способом можно показать, что коэффициент корреляции между полными сибсами тоже равен 0,5. Коэффициенты корреляции не зависят от частот аллелей p1 и q1. Такой результат означает, что родители и дети, а также сибсы имеют 50% общих генов.
Положение становится намного сложнее, если A доминирует над a. В этом случае коэффициент корреляции зависит от частот аллелей. Корреляция родитель - ребенок уже не равна корреляции сибс - сибс, а всегда меньше, за исключением случая q=1.
3.6.1.5. Концепция наследуемости
Концепция наследуемости широко применяется в количественной генетике. Градации изучаемого признака, выраженные в метрических единицах, могут быть названы "значениями". Значение, измеренное у данного индивида, является его фенотипическим значением. Для большинства биологических признаков это фенотипическое значение определяется как генетическими, так и средовыми факторами. Среда рассматривается в широком смысле, т. е. охватывает все негенетические факторы, оказывающие влияние на фенотип (Falconer [63] использует термин средовое отклонение):
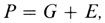
где P - фенотипическое значение, G - генотипическое значение и E - средовое значение.
Фенотипические значения всех индивидов в популяции имеют среднее значение и дисперсию, которая измеряет вариацию вокруг среднего. Дисперсия отличается от других мер изменчивости одним математическим свойством: различные дисперсии можно складывать, получая величину общей дисперсии, и наоборот, общую фенотипическую дисперсию VP можно подразделить на компоненты, такие, как генотипическая дисперсия VG и средовая VE:
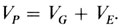
Однако это правило для дисперсии применимо, только если генотипические и средовые значения независимы друг от друга, т. е. когда они некоррелированы. Если между ними имеется корреляция, то следует добавить ковариацию G и E:
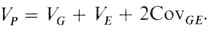
Давайте возьмем один пример из той области генетики, в которой впервые была введена эта концепция - сельскохозяйственные исследования (Falconer [63]). В молочном животноводстве практика кормления коров соответствует их молочной продуктивности: коровам, от которых получают больше молока, дают больше корма. Человеческое общество часто поступает точно так же в отношении своих членов. Этой темы мы коснемся в разделе, посвященном генетике поведения.
Другое предположение состоит в том, что определенные средовые различия имеют одинаковое влияние на разные генотипы. Когда это не так, то существует взаимодействие между генотипом и средой, которое дает дополнительную компоненту VI в общей дисперсии. Даже для экспериментальных животных эта компонента может быть измерена только при особых условиях.
Генотипическая дисперсия VG может быть подразделена на несколько компонент: аддитивную компоненту (VA) и компоненту (VD), измеряющую отклонение от ожидаемого значения в аддитивной модели, которое возникает вследствие доминирования и эпистаза. В доминантную дисперсию вносят вклад гетерозиготы (Aa), которые не занимают строго промежуточного положения между соответствующими гомозиготами (aa и AA). Вклад в дисперсию, осуществляемый эпистазом, относится к действию тех генов, которые влияют на экспрессию других генов. Следовательно, концепция аддитивной дисперсии не подразумевает допущения чисто аддитивного действия генов. Даже действие генов, обнаруживающих доминирование и эпистаз, проявляет тенденцию иметь аддитивную компоненту. Таким образом, в общей фенотипической дисперсии можно выделить следующие компоненты:
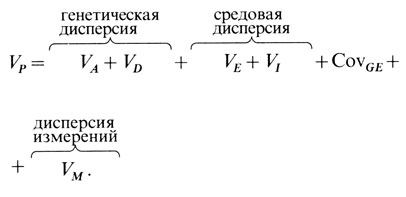
Здесь введена новая компонента (VM), которая относится к варьированию измерений одного и того же признака в разное время. Это могут быть результаты разных опытов в разные дни, или ошибки измерений при тестировании одного и того же образца крови, или различия в повторных обследованиях одного и того же индивида. Если все эти переменные известны, то их тоже можно включить в вычисления. Далее, можно предложить, что ковариация между наследственностью и средой (CovGE) и дисперсия взаимодействия (VI) равны нулю и их можно опустить. Для простоты мы будем полагать также, что компонентой воспроизводимости (VM) можно пренебречь (мы рассмотрим ее позже в разделе, посвященном близнецовому методу, см. прил. 6).
Для удобства полезно ввести новое понятие - понятие наследуемости, которое определяется так:
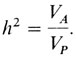
Коэффициент наследуемости принимает значения от 0 до 1 (или от 0 до 100%) и выражает вклад аддитивных генетических факторов в изучаемый фенотип. Другими словами, можно сказать, что наследуемость - это популяционный статистический параметр, который выражает (аддитивный) генетический вклад в изучаемый признак в процентах. Низкое значение наследуемости подразумевает малый вклад аддитивно действующих генов в признак, тогда как высокое значение - большой вклад. Эта концепция была развита в связи с селекцией растений и животных, в частности, таких экономически полезных признаков, как молочная продуктивность коров и яйценоскость кур. Для этих целей наиболее важной была аддитивная часть генетической изменчивости. Любая другая генетическая компонента, такая, например, как доминирование, снижает точность предсказания значений признака у потомства по значениям признака у родителей. Что касается человека, то мы больше интересуемся общей генетической изменчивостью: является ли она вся аддитивной или нет.
В генетике человека наследуемость, как она была определена выше, часто называют "наследуемостью в узком смысле" и дополняют другим понятием:
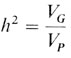
где VG и VP относятся к общей генотипической и фенотипической дисперсии соответственно. Это определение известно как "наследуемость в широком смысле" или степень генетической детерминации.
Существует соотношение между наследуемостью в узком смысле (h2N) и теоретическим коэффициентом корреляции между родственниками, как он определялся и вычислялся выше (3.5).
Для наиболее важных степеней родства принимаются следующие формулы:

Свойства h2. Для интерпретации биологического смысла оценки наследуемости необходимо тщательно рассмотреть ее свойства.
- Наследуемость - это отношение. Оно изменяется, если изменяется числитель или знаменатель, h2 увеличивается, когда увеличивается числитель (генотипическая VG или аддитивная VA дисперсии) или уменьшается средовая дисперсия VE.
- Оценка дисперсии основывается на теоретических корреляциях между родственниками. Эти корреляции справедливы только в предположении случайного скрещивания. Ассортативное скрещивание приводит к другим корреляциям, и если оно не учитывается, то это порождает систематические ошибки в оценке h2. Корреляции при ассортативном скрещивании впервые были вычислены Фишером [664], а также Кавалли-Сфорца и Бодмером [36]: более полная модель описана Вильсон [955; 956]. Эти корреляции можно использовать для коррекции оценок h2.
- Оценка h2 возможна только в том случае, когда делается предположение, что ковариация и взаимодействие между генетическим значением и средовым отклонением равны нулю.
Фалконер попытался избежать этой дилеммы для ковариации, сделав следующее допущение: если проявление генетической конституции индивида модифицируется средовыми условиями, "улучшая" или "ухудшая" его фенотип, то этот вклад можно включить в генотипическое значение как его часть. Формально это правильно, даже если такое допущение усложняет проблему взаимоотношений генотипа и фенотипа. В селекции животных это допущение может быть полезным, но в генетике человека его применение недопустимо.
Еще большие трудности возникают, когда эти концепции применяются для интерпретации значений наследуемости, получаемых на основе близнецовых данных (приложение 6). Компонента в разложении дисперсии, связанная с взаимодействием, приводит к другой трудности в интерпретации, которая до сих пор еще не преодолена.
3.6.1.6. Один пример: рост
Примером биометрического анализа, в котором осуществлена оценка наследуемости, является классическая работа Гальтона по наследованию роста (данные из работы Йохансена [726]). Он измерил рост 204 супружеских пар и 928 их взрослых детей. Имелось, однако, одно методологическое осложнение, состоящее в том, что рост женщин в среднем меньше, чем рост мужчин. Гальтон преодолел эту трудность, умножив все измерения женщин на 1,08, приведя их, таким образом, в соответствие с измерениями мужчин: средний рост мужчин в его выборке был в 1,08 раз больше, чем средний рост женщин. Проведя такую коррекцию, он определил для каждой супружеской пары значение среднего родителя: 1/2 (♂+♀). Результат исследования виден в корреляции данных из табл. 3.17. Корреляция очевидна уже на первый взгляд, и ее величина оказалась достаточно высокой: rpc=0,59 p<0,01, где rpc обозначает корреляцию "средний родитель - ребенок".
Это значение можно использовать для вычисления h2. Наследуемость равна

При случайном скрещивании это дает
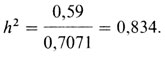
Очевидно, что рост в основном детерминирован генетически, но существует компонента величиной 0,166=1-0,834, не учитываемая аддитивной генетической дисперсией. Это может быть следствием главным образом "средовых факторов". Говорят ли эти данные о каком-либо влиянии среды?
Те же данные можно представить иначе (табл. 3.17 и 3.18). Иным в этом случае будет и характер расхождения с теоретически ожидаемыми значениями. При аддитивном действии генов среднее значение признака у детей должно быть равно полусумме родительских значений, т. е. должно совпадать со средним значением признака у родителей. Однако это не так, имеющиеся данные обнаруживают другую закономерность: если среднее значение признака у родителей выше популяционной средней, то среднее значение признака у детей оказывается меньше родительской средней. С другой стороны, если среднеродительское значение ниже популяционной средней, то среднее значение признака у детей выше такового среди родителей. Итак, среднее значение признака у детей имеет тенденцию к отклонению от родительской средней в направлении популяционной средней.
![Таблица 3.18. (Johannsen, 1926 [726])](pic/000255.jpg)
Таблица 3.18. (Johannsen, 1926 [726])
Это явление было описано Гальтоном и названо им "регрессией на среднюю". Оно имеет место и для других непрерывно распределенных признаков (рис. 3.56).
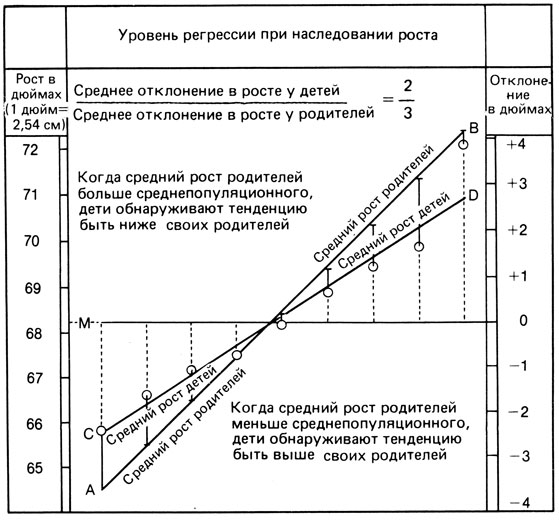
Рис. 3.56. Корреляция по росту между средним родителем и ребенком; регрессия на среднюю. (Чертеж и надписи Гальтона.)
Какова же причина такого расхождения с теоретически ожидаемыми значениями? Вероятно, те индивиды, которые "располагаются" на периферии кривой распределения, несут генетические факторы, обусловливающие крайний фенотип, и, кроме того, находятся под влиянием необычных условий среды. Можно предположить также, что за проявление крайних фенотипов ответственны специфические межгенные взаимодействия и взаимодействия генов и среды. Маловероятно, что дети таких индивидов извлекут пользу из тех условий среды и генотип-средового взаимодействия, которые "поместили" их родителей в крайние классы распределения. Гораздо более вероятно, что фенотипические значения признака у детей будут в большей степени походить на популяционную среднюю, т. е. будет иметь место регрессия на среднюю.
3.6.1.7. Количественная генетика; концепции Менделя и Гальтона
Как связаны между собой две концепции, на которых основывается генетика человека? Представление о гене возникло на основе экспериментов Менделя (разд. 1.4), концепция Гальтона опирается на корреляцию между родственниками и регрессионный анализ. Теоретически между ними можно найти связь, в частности, корреляции среди родственников можно интерпретировать в терминах действия индивидуальных генов, как это впервые детально было показано Фишером (1918) [664]. Биометрический анализ корреляций может дополнить генетический анализ.
Как уже упоминалось во введении, длительный успех научной теории зависит в основном от ее ценности, т. е. от глубины объясняющей мощи. Следовательно, полезно сравнить две концепции в отношении значимости их теоретических основ, используя некоторые критерии, развитые в философии науки [243]. В соответствии с Бунге (1967) "основные требования, предъявляемые к научной теории, следующие: 1) она должна систематизировать знания путем установления логических отношений между отдельными, ранее несвязанными фактами; в частности, объяснять эмпирические обобщения путем получения их из гипотез более высокого уровня; 2) объяснять факты с помощью систем гипотез, из которых вытекают утверждения, отражающие эти факты; 3) углублять знание путем формирования новых утверждений (например, предсказаний) на основе относящейся к предмету информации; 4) повышать тестируемость гипотез, подвергая каждую из них проверке с помощью других гипотез общей системы..."
"Некоторые научные теории не только согласуются с основными требованиями (1)-(4), но, кроме того, могут: 5) направлять исследования либо (а) формулируя или переформулируя актуальные проблемы, либо (б) предлагая сбор новых данных, немыслимых вне этой теории, либо (в) предлагая существенно новые направления исследования; 6) структурировать некоторую область реальности, т. е. давать представление... о реальных объектах, а не просто некую сумму данных и способ их получения".
Бунге привел дарвиновскую теорию эволюции в качестве примера теории, которая удовлетворяет всем перечисленным выше критериям. Вообще способность теории решать задачи зависит от ее глубины. Глубину научной теории оценивают по: уровню обобщений, наличию механизма и объясняющей силе. Действительно, только посредством формулирования далеко идущих (трансэмпирических) концепций, на основе которых можно раскрыть "механизмы" того, что скрыто в глубинах.
Менее глубокие теории называют "феноменологическими" в отличие от теорий, выдвигающих в качестве гипотез определенные "механизмы". (Их часто называют "репрезентационными" или "механизменными".) Такие глубокие механизменные теории вознаграждают своих создателей: оказывается, что их объясняющая сила простирается за пределы того явления, ради которого они были созданы.
Когда теории, развитые на основе концепций Гальтона и Менделя, сравнивают по этим критериям, то оказывается, что гальтоновский подход породил феноменологическую теорию. Пирсон, знаменитый ученик Гальтона, еще в 1904 г. указывал, что количественное сравнение фенотипов родственников с помощью биометрических методов ведет к "чисто описательной статистической теории". До определенной степени она систематизирует знания, но выдвигает неспецифические гипотезы. На ее основе сходство между родственниками можно объяснить наследственностью или, более определенно, аддитивным генным действием без или с вкладом доминирования или средовых факторов. Такие утверждения носят слишком общий характер, и только дополнительные гипотезы могут иногда усилить их значимость. В качестве примера можно привести эффект Картера, описанный в разд. 3.6.2.3: более высокая частота врожденных дефектов у родственников пробандов-женщин была предсказана и объяснена дополнительной гипотезой об идентичности распределения генов подверженности у обоих полов, несмотря на неравное распределение по полу среди пробандов. Условия 5) и 6) для концепции Гальтона вовсе не выполняются: проблемы нельзя переформулировать в более плодотворной форме и теория не предлагает способа получения новых данных. Она предлагает лишь очевидное: сравнение родственников.
Обратимся к результатам, полученным последователями Менделя. Вскоре после переоткрытия его законов было сформулировано представление о единице наследования, рекомбинации и функции, которая теперь называется "геном". Благодаря этому был открыт путь для исследования механизмов репликации, рекомбинации и действия генов. Поэтапное раскрытие этих механизмов составило, по-существу, историю генетики и до сих пор является предметом ее исследований. Теория Менделя объясняет не только передачу признаков от родителя детям, но и в ряду поколений различных клеток организма.
Объясняющая мощь этой теории еще не исчерпана. Возвращаясь к нашей классификации генетического анализа (т. е. на уровне ДНК - генный уровень, на уровне генного продукта - биохимический уровень, на качественном фенотипическом уровне, на уровне количественного фенотипа - биометрический уровень), можно сказать, что гальтоновский биометрический подход дает ответы на уровне, дальше всего отстоящем от генного действия. Другими словами, исследования с помощью методов биометрической генетики руководствуются теорией "черного ящика". Две внешние наблюдаемые переменные (измерения признака у родителей и детей или других групп родственников) сравниваются друг с другом, но промежуточная биохимическая переменная неизвестна и остается в "черном ящике" (рис. 3.57).
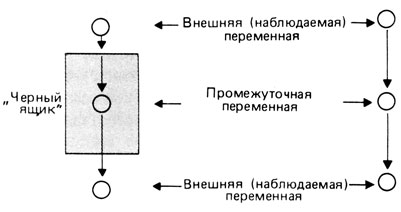
Рис. 3.57. Отличия гипотезы 'черного ящика' и механизменной гипотезы. В гипотезе 'черного ящика' (слева) промежуточная переменная, лежащая в основе влияния одной наблюдаемой переменной на другую, остается неизвестной. В механизменной гипотезе (справа) промежуточную переменную можно дедуцировать (предположить) на основе научной теории, а затем предложить механизм, посредством которого одна наблюдаемая переменная влияет на другую
Все в человеке - его развитие, строение и функции - в конечном счете контролируется генами. Различия между людьми можно продемонстрировать указанием на физиологические, биохимические и иммунологические особенности каждого индивида. Генетическую детерминацию этих особенностей можно показать с помощью семейного анализа. У монозиготных близнецов все гены являются идентичными, вот почему такие близнецы будут больше походить друг на друга, чем любые другие родственники. У сибсов 50% общих генов, тогда как у более отдаленных родственников лишь малая часть генов является общей.
Сравнение родственников на основе биометрических методов анализа фенотипа, вероятно, должно ответить на вопрос, лежат ли в основе этого признака генетические факторы. "Наследуемость" или доля общей изменчивости, приписываемая генетической причине, обычно оценивается величиной, большей нуля. Поскольку главная биологическая основа поведения человека связана с мозгом, а мозг, как любой другой орган, обнаруживает генетическую изменчивость, вероятно, должны существовать и генетические факторы, определяющие поведение. Для поведенческих признаков особенно трудно отделить действие общих генов от действия общей среды в семье, что, в частности, ведет к трудностям в интерпретации.
Однако анализ любого признака человека, и в особенности поведенческого, может дать больше существенной информации, если фенотип исследуется с помощью менделевского подхода на уровне генного действия. "Черный ящик", таким образом, открывается, и неизвестная промежуточная переменная заменяется известным биохимическим механизмом.
В свете существенных различий научной значимости обеих теорий уместно, пожалуй, задать вопрос, почему множество работ в генетике человека все же использует гальтоновский подход? Большинство признаков человека, в особенности поведенческих и таких, как подверженность заболеваниям, просто не могут изучаться на основе менделевских принципов. Их использование предполагает, что изучаемый признак четко очерчен, для чего часто необходимо применение весьма сложных биологических методик всех типов. Выбор таких признаков требует специальных знаний из области нормальной биологии и патологии человека и применения методов различных медико-биологических наук. С другой стороны, часто нетрудно подсчитать и измерить некий простой и очевидный количественный признак. Вот почему гальтоновский подход нередко служит первым шагом к дальнейшему анализу и может иногда привести к практически полезным результатам, несмотря на ограниченность самой теории.
Кроме того, гальтоновский подход продолжает быть важным для формулирования гипотез, для выбора признаков, которые будут изучаться более точными методами, и для разработки исследовательских стратегий. Признаки человека, контролируемые большим числом генов, каждый из которых вносит свой небольшой вклад в общую изменчивость, трудны для изучения на основе менделевского подхода. Следует помнить, однако, что для некоторых таких признаков аддитивно-полигенная модель может оказаться неадекватной. Вполне вероятно, что генетический контроль обеспечивается одним или несколькими генами с большим эффектом, который можно выявить индивидуально с помощью биологических методов, а остальные гены образуют всего лишь "генетический фон".
Итак, гальтоновский подход следует использовать, если нет альтернативы. Но не следует превращать его в самоцель. Вряд ли нужно с помощью компьютеров разрабатывать крайне сложные статистические подходы к вычислению коэффициентов наследуемости, чтобы оценить вклад различных наследственных, общесемейных и экономических факторов в изменчивость фенотипа или сравнить генетические модели без или с участием главных генов. Конечный результат таких упражнений часто оказывается неудовлетворительным, поскольку биологи нуждаются в более конкретных данных. Статистические методы, конечно, имеют огромное значение для генетического анализа человека, но они должны использоваться для проверки биологически хорошо обоснованных гипотез, сформулированных на основе мощной биологической теории. Для более глубокого понимания биологии человека сложные статистические методы, используемые в анализе количественных признаков (на биометрическом уровне), на наш взгляд, менее полезны, чем более простые методы, применяемые в генетическом анализе на генном или биохимическом уровне.
Об этом необходимо помнить при знакомстве со следующим разделом, в котором будут излагаться более сложные модели наследования.
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'