
1.2. Тетрадный анализ
1.2.1. Нормальное расщепление диплоидов
Для выделения образовавшихся при мейозе спор (аскоспор, базидий) часто используют микроманипулятор. В этом случае (а также при расщеплении по гену, определяющему окраску аскоспор) можно проанализировать расщепление, происходящее в каждом мейозе, учтя генотипы спор в образовавшей их тетраде. Данный метод анализа расщепления называется тетрадным анализом. Суть его заключается в том, что споры, образовавшиеся в результате разных мейозов, не перемешиваются, а расщепление учитывается в каждой четверке (или четырех парах, если аски восьмиспоровые) спор, образовавшихся при мейозе из одной диплоидной клетки. Очевидно, такой анализ возможен тогда, когда при мейозе образуются четыре жизнеспособные гаплоидные клетки и когда эти клетки остаются какое-то время соединенными, не распадаясь и не перемешиваясь со спорами иного происхождения.
Различают упорядоченные тетрады спор - аски, в которых споры лежат в том порядке, как происходило расхождение наборов хромосом в двух делениях созревания, и неупорядоченные, где расположение спор случайно и не отражает порядка расхождения наборов. Упорядоченные тетрады свойственные тем аскомицетам, которые образуют линейные аски, в частности Neurospora, Sordaria, Podospora, у которых четыре пары спор располагаются в ряд. Такие аски иногда образуются и некоторыми штаммами дрожжей-сахаромицетов, которым, однако, более свойственны неупорядоченные тетрады. Последние характерны также и для Aspergillus, Ascobolus, базидиомицетов.
В общей форме основы тетрадного анализа были сформулированы в 1949 г. независимо несколькими авторами [27, 36, 42]. В дальнейшем теория тетрадного анализа подвергалась детальной математической разработке 18, 12, 50 и др.].
Рассмотрение теории тетрадного анализа удобнее начать с моногибридного скрещивания. Если две гаплоидные формы отличаются альтернативным признаком, обусловленным одним геном (аллели А и а), распределяющимся в мейозе с хромосомами, то при скрещивании таких форм в каждой тетраде наблюдается расщепление 2:2. В случае упорядоченных асков споры располагаются в порядке ААаа. Порядки спор АааА или АаАа и другие получаются, если между центромером хромосомы и локусом A/a произошел кроссинговер.
Разное расположение спор в аске (некроссоверное и кроссоверное) исторически получило следующие наименования: расщепление при I делении (в дальнейшем сокращенно обозначается рIд; АAаа, ааАА) и расщепление при II делении (рIIд, АаАа, аАаА, АааА, аААа). Различить их можно лишь при анализе упорядоченных асков. Математически рIIд в два раза вероятнее, чем рIд, и должно наблюдаться в два раза чаще. Практически они появляются с частотой 0,67 и 0,33 тогда, когда ген А настолько удален от центромера, что кроссинговер на участке OA происходит с большой частотой (здесь и в дальнейшем О обозначает центромер).
При скрещивании форм, отличающихся двумя факторами, в тетрадах наблюдается следующее расщепление:
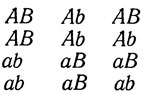
Эти типы тетрад получили соответствующие наименования: родительский дитип (Р), неродительский дитип (N) и тетратип (Т). При независимом расщеплении двух генов, каждый из которых достаточно удален от центромера, ожидается соотношение типов тетрад 1P : 1N : 4Т. Его можно вывести из результатов, представленных в табл. 1.2. Типы тетрад Р, N и Т возникают при различных сочетаниях рIд и рIIд по гену А с рIд и рIIд по гену В. Обозначим fIA и fIIA частоты расщепления гена А при I и II делениях (fIB и fIIB соответственно для гена В). Если fIA = 0,33; fIIA = 0,67; fIB = 0,33; fIIB = 0,67, то по табл. 1.2 может быть легко вычислена вероятность возникновения тетрад Р, N и Т. Получаем
fP = fN, fТ = 0,67,
где fP, fN, fT соответственно частота появления тетрад типов Р, N, Т. Хотя приводимые в табл. 1.2 расщепления по А- и B-генам различимы лишь в упорядоченных тетрадах, они происходят и при образовании неупорядоченных тетрад. В упорядоченных тетрадах при дигибридном скрещивании можно различить большое число типов тетрад (отличающихся порядком спор), в неупорядоченных - только три - Р, N и Т.
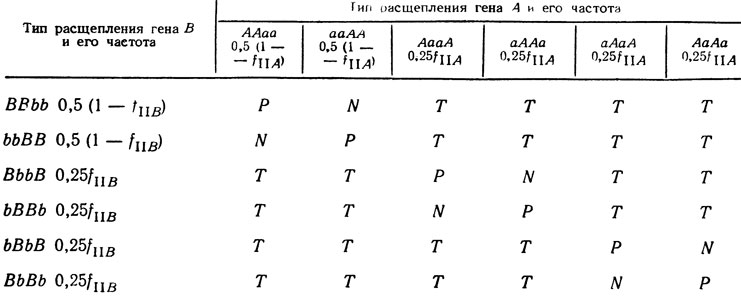
Таблица 1.2. Образование различных типов тетрад в дигибридном скрещивании в зависимости от типа расщепления первого и второго генов
(Примечание Частота расщепления при втором делении - fII, четыре возможных при этом порядка спор возникают с равной вероятностью; частота расщепления при первом делении - fI = 1 - fII два возможных при этом порядка спор возникают с равной вероятностью)
В тригибридном скрещивании при анализе неупорядоченных тетрад различимы 12 типов расщеплений (первый символ - тип тетрады по паре АВ, второй - по паре ВС):
1. РР 4. NP 7. TP 10. ТТ 2. PN 5. NN 8. TN 11. ТТ 3. РТ 6. NT 9. ТТ 12. ТТ.
Расщепление в типах 9-12 следующее:
AВС, АbС, аВс, аbс; ABC, Abc, аВс, abC; АВс, Abc, аВС, abC; АВс, AbC, аВС, abc.
Если в дигетерозиготе гены А и В сцеплены, то среди тетрад также различимы типы Р, N, Т. Появляются они, однако, не в соотношении 1:1:4, так как N и Т содержат кроссоверные хроматиды и, следовательно, будут возникать реже, чем если бы гены А и В наследовались независимо. Сцепление таким образом устанавливается, если
fP > fN; fT < 0,67.
Практически опытные данные сравнивают с теоретически ожидаемым отношением при независимом наследовании с помощью статистического метода χ2. Специально для тетрадного анализа соответствующие формулы были выведены Н. Н. Хромовым-Борисовым:
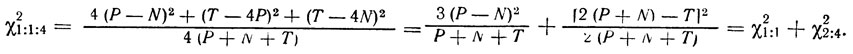
Здесь Р, N и Т - число соответствующих тетрад, проанализированных в эксперименте. Вычисленное по этой формуле значение χ2 сравнивается с данными таблицы при числе степеней свободы df = 2.
Можно проверять отдельно соответствие соотношений Р : N и (Р + N) : Т ожидаемому. С поправкой на дискретность формула
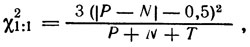
применима уже при (Р - N) ≥ 8, а формула
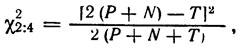
при [2 (Р + N) - T] ≥ 30 (поправка на дискретность в этом случае не является постоянной и поэтому не используется).
Как указано, эти формулы применимы при определенном значении разности Р - N и (Р + N) - Т. Если в эксперименте значение разности оказалось меньше требуемой, а увеличить число анализируемых тетрад затруднительно, то следует обратиться к специальным таблицам, составленным Н. Н. Хромовым-Борисовым и М. И. Рахманом, которые приведены в работе И. А. Захарова и соавт. (Прил. 15) [4].
Если установлено сцепление для трех или более генов, можно определить их порядок, т. е. решить первую задачу генетического картирования. Для этого не обязательно прибегать к каким-либо специальным вычислениям. Предположим, сцепление установлено для генов А, В, С. Они могут быть расположены в порядке А - В - С, А - С - В или В - А - С. Рекомбинация этих генов может быть результатом одиночного или двойного обменов. Посмотрим, какие типы тетрад в отношении пар генов А - В, В - С и А - С дадут двойной обмен при перечисленных трех порядках генов, считая родительскими генотипы АВС и abc. Это ТТР, РТТ, ТРТ. Двойные обмены совершаются намного реже, чем одиночные. Поэтому достаточно посмотреть, какой класс из возможных при тригенном расщеплении появлялся существенно реже, чем все остальные, чтобы сразу определить порядок генов (обсуждение вопроса см. [45]).
У Neurospora crassa проанализировано расщепление по генам А, ad, vis (табл. 1.3, 1.4). Из этих данных следует, во-первых, что все три гена сцеплены и во всех случаях соотношение Р : N сильно отличается от 1:1; во-вторых, в зависимости от порядка генов двойные обмены дадут тетрады ТРТ, РТТ, ТТР. Два последних класса встречаются часто (171 и 85 асков). Очевидно, они не могут быть результатом двойного обмена. Первый же класс редок, на основании чего можно вывести порядок генов А - ad - vis.
![Таблица 1.3. Расщепление по трем сцепленным генам A, ad, vis расщеплении у нейроспоры [16]](pic/000010.jpg)
Таблица 1.3. Расщепление по трем сцепленным генам A, ad, vis расщеплении у нейроспоры [16]
![Таблица 1.4. Суммарное число разных типов тетрад для пар генов при тригенном у нейроспоры [16]](pic/000011.jpg)
Таблица 1.4. Суммарное число разных типов тетрад для пар генов при тригенном у нейроспоры [16]
Теперь рассмотрим задачу определения расстояния между генами. Если установлено сцепление, то можно определить частоту рекомбинации между генами. Частоту рекомбинации сцепленных генов А и В обозначим rАВ. На участке А - В может происходить как одиночный, так и множественный кроссинговер. Если пренебрегать возможностью тройных (и более высокой степени) обменов, то последствия разных типов обменов можно представить так, как это сделано на рис. 1.1. Видно, что двухроматидный двойной обмен вообще не выявляется (тетрада Р), а трихроматидные двойные обмены (тетрады Т) смешиваются с одиночными. Указанные на рисунке четыре типа двойных обменов возникают c равной вероятностью, следовательно, среди двойных обменов соотношение четырехроматидные : трихроматидные : двухроматидные составляет 1:2:1, причем частота четырехроматидных двойных обменов - fN, трихроматидных, следовательно, 2fN, двухроматидных fN. Отсюда следует, что частота тетрад с двойными обменами - fN + 2fN + fN; тетрад с одиночными обменами - fT - 2fN; некроссоверных fP - fN, откуда;
rAB = 4fN + 0,5 (fT - 2fN) = 3fN + 0,5fT. (1)
Данная формула учитывает возможность прохождения двойных обменов, но игнорирует возможность прохождения множественных (тройных, четверных и так далее). Здесь, таким образом, в скрытом виде присутствует предположение об интерференции, т. е. взаимовлиянии обменов, делающем маловероятным прохождение множественных обменов. Когда интерференция учитывается тем или иным образом, то рассчитанная частота рекомбинации принимается мерой генетических расстояний, оценивая их в особых единицах, названных сантиморганами. Этой единице можно дать следующее определение. Морган (название в честь создателя хромосомной теории наследственности) - генетическая длина отрезка хроматиды, на котором в среднем в мейозе происходит один обмен [41]. Одна сотая этой длины - сантиморган (сМ) - в отечественной литературе прежде именовалась морганидой - название, которого во избежание путаницы теперь следует избегать. На малых отрезках 1 сМ соответствует 1 % наблюдаемой в опыте частоты рекомбинации.
Можно, однако, не принимать во внимание интерференцию, считая, что обмены по длине хромосомы происходят независимо друг от друга. Такая предпосылка позволяет развить простую математическую теорию рекомбинации [19]. Можно предположить, что вероятность разного числа обменов для данной пары гомологичных хромосом или для какого-либо их участка соответствует закону Пуассона: в совокупности мейозов биваленты без обменов появляются с вероятностью Р0, с одним обменом - с вероятностью Р1 и т. д., причем
P0 = e-x, P1 = xe-x, Pn = xne-x/n!
где е - основание натуральных логарифмов; х - среднее число обменов на бивалент (или на его участок); n - произвольное число.
Из рис. 1.1 видно, что биваленты без обменов не дают рекомбинантных хроматид. Биваленты с одним обменом дают каждый две родительские и две рекомбинантные хроматиды, т. е. по 1/2 общего числа хроматид, берущих начало от таких бивалентов. Биваленты с двумя (а также с тремя и более) обменами в сумме дают 1/2 родительских и 1/2 рекомбинантных хроматид. Вероятность бивалентов с одним и более обменами составляет 1 - е-x. Частота рекомбинантных хроматид оказывается тогда
r = 1/2( 1 - е-x)
или
r = 1/2( 1 - е-2D/100) (2)
если D - расстояние, измеренное в сантиморганах, причем D = 50x:. Эта формула может быть переписана в другом виде, более удобном для выполнения расчетов:
D = - 50 ln (1 - 2r). (3)
Учитывая происхождение тетрад Р-, N-, Т-типов, их частоты можно вывести аналогичным образом и связать с генетическим расстоянием:
D = - 50 ln (fP - fN), (4)
D = - 33,33 ln (1 - 1,5fT) [12]. (5)
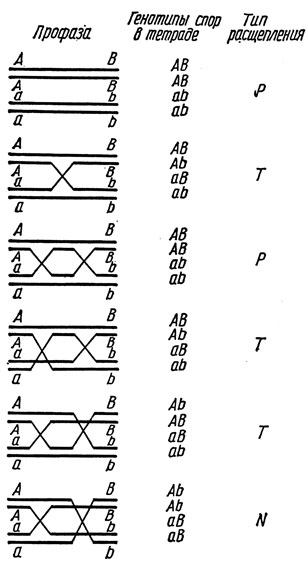
Рис. 1.1 Расщепление при разных типах кроссинговера: 1 - без кроссинговера; 2 - кроссинговер одиночный; 3 - двойной двукроматидный; 4-5 - двойной трихро. матидный; 6 - двойной четырехроматидный
При использовании приведенных формул генетические расстояния измеряются в единицах, названных стрейнами [28]. Формула (2), выражающая основной закон генетической рекомбинации, была впервые выведена выдающимся английским генетиком Холдейном [19]. Название "стрейн" является сочетанием букв его фамилии и фамилии Стертеванта, доказавшего линейное расположение генов в хромосоме. При небольших расстояниях - до 10 единиц - стрейн равен сантиморгану. Сейчас предпочитают пользоваться второй из этих двух единиц.
Естественно, возникает вопрос, а как обстоит дело с интерференцией в действительности. В отличие от обычного генетического анализа случайной выборки гамет тетрадный анализ позволяет выявлять два вида интерференции. Это, во-первых, хиазмовая интерференция - взаимовлияние обменов в биваленте, независимо от того, какие хроматиды в них участвуют. Хиазмовая интерференция положительна, если один обмен уменьшает вероятность другого, и отрицательна, если увеличивает. Во-вторых, хроматидная интерференция - отклонение от случайного участия четырех хроматид во множественных обменах в одном биваленте, т. е. отклонение от ожидаемого соотношения 1:2:1 разных типов двойных обменов (см. рис. 1.1). Хроматидная интерференция положительна, если один обмен с участием дан-ной хроматиды уменьшает вероятность участия этой хроматиды во втором обмене. Хроматидная интерференция отрицательна, если один обмен увели-чивает вероятность участия хроматиды в другом обмене. Интерференция, которую обнаруживают при анализе случайной выборки хроматид, является результирующей, объединяющей эффекты хиазмовой и хроматидной интерференции.
Анализ особенно многочисленных данных по кроссинговеру у Neurospora crassa, а также у 10 других видов грибов, показал, что во всех случаях хиазмовая интерференция положительна [37]. Единственным исключением является Aspergillus nidulans, у которого хиазмовая интерференция не обнаружена.
Статистически значимое отклонение от соотношения 1:2:1 для трех типов двойных обменов, идентифицируемых при тетрадном анализе расщепления по трем маркерам, свидетельствует о хроматидной интерференции. Анализ экспериментальных данных [16] показывает, что в целом они соответствуют ожидаемому соотношению, хотя в отдельных исследованиях были замечены существенные отклонения.
Итак, при расчете истинных генетических расстояний (D'), должны приниматься во внимание эффекты интерференции. Был создан ряд математических моделей, учитывающих интерференцию и позволяющих по наблюдаемой частоте рекомбинации или по частотам тетрад разного типа рассчитать истинные генетические расстояния [8]. Обычно вычисления оказываются сложными и требуют применения ЭВМ [48, 49]. Сейчас, однако, предложена простая эмпирическая формула, которая позволяет легко вводить при расчете расстояния поправку на интерференцию. Если расстояние D рассчитано по формуле (1) (при D = 100r), то D' будет
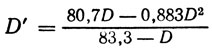 (6)
(6)(необходимые вычисления без труда делаются с помощью микрокалькулятора). На рис. 1.2 приведен график зависимости D' от D и соответствующие экспериментальные точки. При определении расстояний можно пользоваться также и этим графиком.
![Рис. 1.2. Зависимость истинного значения генетического расстояния (D') от расчетного (D) [30]: Точки - экспериментальные данные, кривая соответствует уравнению (6)](pic/000014.jpg)
Рис. 1.2. Зависимость истинного значения генетического расстояния (D') от расчетного (D) [30]: Точки - экспериментальные данные, кривая соответствует уравнению (6)
Преимущество тетрадного анализа перед анализом случайной выборки состоит в том, что его методами можно определить сцепление гена и центромера, т. е. генетическими методами определить локализацию центромеров в группах сцепления. Наиболее просто это осуществляется при анализе расщеплений в упорядоченных тетрадах. Как указывалось, рIIд по гену А наблюдается в том случае, если между локусом А и центромером (О) произошел кроссинговер. Тетрады, обнаруживающие рIIд, содержат две кроссоверные и две некроссоверные хроматиды. Таким образом, если не принимать во внимание множественные обмены, частота рекомбинации гена и центромера будет rOА = 0,5fIIA.
Более сложным является установление сцепления с центромером в случае неупорядоченных тетрад. Здесь оно возможно лишь в полигибридных скрещиваниях. Как видно из табл. 1.1, тетратипы возникают тогда, когда по генам А или В наблюдается рIIд. Отсюда если сцепление гена и центромера уменьшит частоту рIIд (fII <0,67), то уменьшится и частота тетратипов. Результаты, представленные в табл. 1.1, показывают, что сохраняется одинаковое число Р и N. Следовательно, о сцеплении с центромерами генов А и В можно судить, если
fP = fN; fT><2(f>P + fN)
(проверять методом χ2).
Установленную зависимость частоты появления различных типов тетрад от расстояния между локусами и центромерами можно выразить алгебраически и дать формулу для определения частоты рекомбинации между генами и центромерами.
С помощью табл. 1.1 можно рассчитать (перемножая частоты по строчкам и столбцам) частоту (в зависимости от fIIA и /fIIB) появления тетрады Р, N и Т. Так, для частоты тетратипов получаем
fT = fIIA + fIIB - 1,5fIIA ⋅ fIIB.
Значение fT можно определить из опыта. Это уравнение, однако, содержит два неизвестных. Поэтому необходимо вести анализ по трем локусам A, B, С, расщепляющимся при II делении соответственно с частотами fIIA, fIIB, fIIC. Тогда
fTAB = fIIA + fIIB - 1,5fIIA ⋅ fIIB
fTAC = fIIA + fIIC - l,5fIIA ⋅ fIIC
fTBC = fIIB + fIIC - 1,5fIIB ⋅ fIIC
Значения fTAB, fTAC, fTBC определяются из опытов, в которых анализировались аски соответствующих гетерозигот. Решив систему уравнений, находим fIIA, fIIB, fIIC. Найденная частота рекомбинации гена и центромера должна быть переведена в расстояние. Для перевода ее в стрейны пользуются формулой:
D = - 33,3 ln (1 - 1,5fII), (7)
а для того, чтобы учесть эффекты интерференции, рекомендуется пользоваться графическим методом. Соответствующий график изображен на рис. 1.3, причем реально наблюдаемой интерференции соответствует кривая, показатель интерференции которой составляет 0,3 [32].
![Рис. 1.3. Зависимость расстояния между геном и центромером (D) от наблюдаемой частоты расщепления при II делении [32]. Цифры на кривых - показатели интерференции; 0 - полная интерференция; 1,0 - отсутствие интерференции](pic/000015.jpg)
Рис. 1.3. Зависимость расстояния между геном и центромером (D) от наблюдаемой частоты расщепления при II делении [32]. Цифры на кривых - показатели интерференции; 0 - полная интерференция; 1,0 - отсутствие интерференции
Расстояние от гена до центромера особенно просто определить при использовании следующего способа [461. Установлено, что частота тетратипов в расщеплении по двум генам есть функция расстояний между этими генами и центромерами, так что сумма расстояний А - 01 и В - 02 равна расстоянию А - В, которое можно определить по частоте тетратипов (5). Тогда
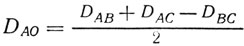 (8)
(8)(расстояние будет выражено в стрейнах).
Упомянутый способ был использован в ряде работ [23, 5]. Определить расстояние между генами и центромерами можно и в том случае, если два из трех анализируемых генов сцеплены друг с другом. Специально этот вопрос был рассмотрен в работе [53]. Там же приводятся способы расчета статистических ошибок найденных значений частот расщепления при втором делении. Ниже даны примеры картирования при тетрадном анализе у грибов.
Практически при проведении тетрадного анализа рекомендуется вводить в скрещивания маркер, очень тесно сцепленный (<1 % рекомбинации) с центромером. Для дрожжей-сахаромицетов такими маркерами могут служить trp1, pet8 или met 14. Тогда для некартированного гена fрIIд приблизительно равна fT с любым из таких маркеров.
В предыдущем примере были приведены данные о расщеплении трех сцепленных генов у нейроспоры. По этим данным определим расстояние между генами (табл. 1.5). Видно, что при достаточно тесном сцеплении вычисления по любой из формул дают близкие результаты. Во всех случаях значения получаются аддитивными, т. е. расстояние А - vis равно сумме расстояний А - ad и ad - vis.
Таблица 1.5. Сравнение (в случае сильного сцепления) результатов измерения расстояний между генами, сМ (1), (6) и стрейн (4), (5)
Гибрид дрожжей-сахаромицетов, гетерозиготный по генам V хромосомы, показал следующее расщепление (табл. 1.6). Как и в предыдущем примере, сцепление генов his 1 - ilv 1 и cho 1 - his 1 сомнения не вызывает. Насколько, однако, достоверно отклонение от независимого расщепления генов cho 1 и ilv 1? Воспользуемся следующей формулой для определения χ21:1:
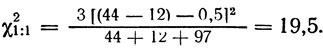
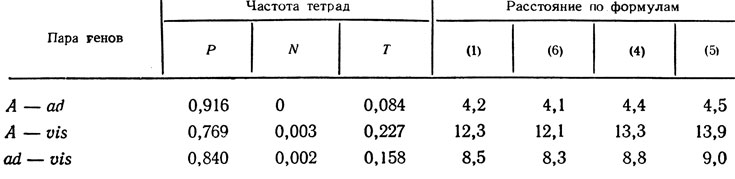
Таблица 1.5. Сравнение (в случае сильного сцепления) результатов изменения расстояний между генами, сМ (1), (6) и стрейн (4), (5)
![Таблица 1.6. Расщепление в потомстве гибрида Sacch. cerevisiae, гетерозиготного по трем генам V хромосомы [45]](pic/000018.jpg)
Таблица 1.6. Расщепление в потомстве гибрида Sacch. cerevisiae, гетерозиготного по трем генам V хромосомы [45]
Полученное значение больше критического (6,63), так что р < 0,01, и может быть сделан вывод: тетрады типа Р и N появились не в одинаковом числе, т. е. гены сцеплены.
Определим частоту тетрад разных типов и расстояние между генами (табл. 1.7). Видно, что при больших расстояниях наблюдается существенная разница между результатами измерений расстояний в сМ и в стрейнах. Первые показывают гораздо большую аддитивность, т. е. предпочтительнее пользоваться формулами (1) и (6), чем (4) и (5).
![Таблица 1.7. Сравнение (в случае слабого сцепления) результатов измерения расстояний между генами, сМ (1), (6) и стрейн (4), (5) [45]](pic/000020.jpg)
Таблица 1.7. Сравнение (в случае слабого сцепления) результатов измерения расстояний между генами, сМ (1), (6) и стрейн (4), (5) [45]
Результаты анализа другого гибрида дрожжей-сахаромицетов представлены в табл. 1.8. Убедимся, что все гены друг с другом не сцеплены, а со своими центромерами сцеплены. Для этого рассчитаем χ21:1 и χ22:4 (см. выше). Во всех случаях соотношение Р : N достоверно не отличается от 1:1 (χ21:1 < 3,84, Р > 0,05), а соотношение (Р + N): Т явно отклоняется от 2:4. Можно сделать вывод, что гены не сцеплены, но показывают сцепление со своими центромерами.
Для дальнейших расчетов необходимы значения fT:
МАТ - ura3 - 0,461
MAT - gal1 - 0,429
ura3 - gal1 - 0,329,
которые позволяют, решив систему трех уравнений определить fII для каждого гена, а также по формуле (7) измерить (в стрейнах) расстояние ген - центромер. Получаем
МАТ : fII = 0,356; D = 25,4 ura3 : fII = 0,225; D = 13,7 gal1 : fII = 0,157; D = 8,9.
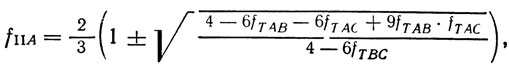
![Таблица 1.8. Анализ расщепления гибрида Sacch. cerevisiae, гетерозиготного по трем генам, каждый из которых сцеплен со своим центромером [12]](pic/000022.jpg)
Таблица 1.8. Анализ расщепления гибрида Sacch. cerevisiae, гетерозиготного по трем генам, каждый из которых сцеплен со своим центромером [12]
Обратим внимание, что приведенное уравнение для fII имеет два алгебраических решения; из них берем меньшее предельновозможного для fII значения - 0,7.
Расстояние может быть также вычислено без определения fII по формуле (8), например, для МАТ
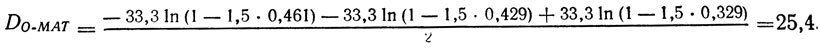
|
ПОИСК:
|
© GENETIKU.RU, 2013-2022
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'
При использовании материалов активная ссылка обязательна:
http://genetiku.ru/ 'Генетика'