3.2.2. Соотношения Харди - Вайнберга доказывают генетическую основу групп крови системы ABO

Множественный аллелизм. До сих пор мы рассматривали в каждом локусе только два разных аллеля. Однако часто встречаются ситуации когда локус может быть представлен более чем двумя аллелями. Примеры такого "множественного аллелизма" описаны и для людей, и для экспериментальных животных. Наиболее известны среди них - серия аллелей локуса white y Drosophila melanogaster и серия альбино-локуса у кроликов.

Важно помнить, что

а) любой индивид может иметь максимум два аллеля из серии (если у него две гомологические хромосомы, а, например, не три, как у трисомиков);

б) кроссинговер между этими аллелями может не учитываться, поскольку они расположены в гомологичных локусах. С уточнениями этого второго условия мы будем иметь дело в разд. 3.5 в связи с обсуждением современных концепций гена. Здесь же будет описана простейшая формальная модель на примере групп крови ABO.

Генетика групп крови ABO. Группы крови ABO были открыты в 1900 г. Ландштейнером [259]. Несчастные случаи, имевшие место при переливании крови, заставили задуматься над причиной и тем самым способствовали открытию системы ABO. Первая разумная генетическая теория предложена фон Дунгерном и Гиршфельдом (1911) [631]. Для объяснения четырех фенотипов A, B, O и AB они предположили наличие двух независимых пар генов (A,O; B,O), где A и B - доминантные аллели. Бернштейн (1925) [574] проверил эту гипотезу, используя прежде всего соотношения, ожидаемые из закона Харди - Вайнберга. Он пришел к выводу об ошибочности их концепции и предложил правильное объяснение - три аллеля с шестью генотипами и четырьмя фенотипами вследствие доминирования аллелей A и B над аллелем O.

Наиболее очевидный способ проверки этих гипотез - обратиться к семейным исследованиям. Однако различия между этими двумя гипотезами ожидаются только для тех браков, в которых по крайней мере один из родителей имеет группу AB (табл. 3.4): двухлокусная диаллельная модель допускает в таких браках наличие детей с группой O, а трехаллельная монолокусная - нет. Хотя группа AB самая редкая, в литературе уже публиковались сообщения о детях с группой крови O у родителей с группой AB (либо группа крови в таких случаях неправильно диагностирована, либо дети внебрачные). Однако эти наблюдения не ввели Бернштейна в заблуждение. Его рассуждения были следующими. Предположим, что справедлива теория двух генов. Пусть p будет частотой аллеля A (1-p=p′ частота аллеля а) и q - частотой аллеля B (1-q=q′ - частота аллеля b). Тогда в популяции следует ожидать такие относительные частоты генотипов и фенотипов:

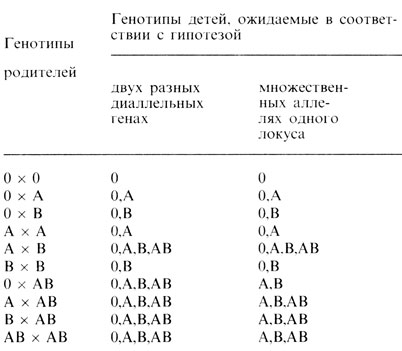
Таблица 3.4. Сравнение двух гипотез о наследовании групп крови ABO. (По Wiener A. S, 1943, с изменениями.)

Это ведет к таким соотношениям (Ā, B̄ - частоты фенотипов):

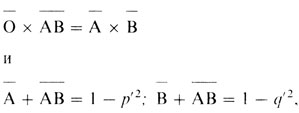
которые дают

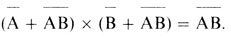
Это равенство можно проверить. Оказалось (и с тех пор все время подтверждается), что

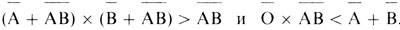
Различия настолько велики (и так убедительны), что их невозможно объяснить случайными отклонениями. Первой альтернативой, рассмотренной Бернштейном, было предположение о гетерогенности изучаемой популяции. Однако это объяснение оказалось недостаточным. С другой стороны, легко показать, что генотипические распределения во всех популяциях, для которых имелись данные, находились в прекрасном согласии с соотношениями, ожидаемыми на основе мультиаллельной монолокусной гипотезы.

Чтобы понять рассуждения Бернштейна, следует по-новому взглянуть на закон Харди - Вайнберга. Он был выведен нами для специального случая двух аллелей. Однако можно показать, что этот закон применим и ко многим аллелям. Если обозначить частоты n аллелей как p₁, p₂, ..., p_n, то относительные частоты генотипов задаются разложением (p₁+p₂+...+p_n)². Для конкретного случая аллелей A, B, и O с частотами p, q и r отсюда следует, что распределение генотипов имеет вид

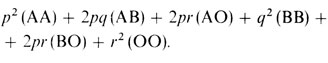
Для четырех классов фенотипов

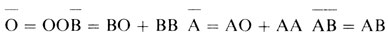
можно получить следующие вероятности:

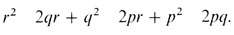
Отсюда следует

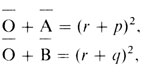
поэтому

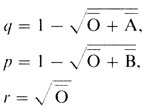
и справедливо соотношение

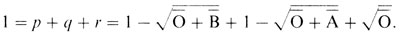
Это равенство можно проверить, используя распределения фенотипов ABO в различных популяциях мира. Критерием служит равенство единице суммы аллельных частот, вычисленных по приведенной выше формуле. Кроме того, на основе получаемых частот аллелей можно вычислить ожидаемые частоты генотипов и сравнить их с наблюдаемыми. Помимо корректности самой генетической гипотезы этот результат подлежит проверке на выполнение другого условия: в популяции по изучаемому признаку должно быть случайное скрещивание (панмиксия).

Для данных, анализированных Бернштейном, уже было получено превосходное соотношение, и это подтвердилось для огромного количества накопленных с тех пор материалов. Для понимания принципа вычисления приведем один пример. В Берлине были найдены следующие фенотипические частоты групп крови.

По формуле Бернштейна получаем частоты аллелей:

Итак, p+q+r=0,9991.

На первый взгляд этот результат хорошо согласуется с ожидаемым значением 1. В качестве статистического критического критерия для тестирования значимости отклонения можно использовать метод хи-квадрат [625]:

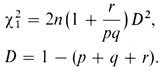
В нашем примере χ²₁=0,88, что явно меньше граничного значения χ²₁=3,84 при одной степени свободы (для 5%-ного уровня значимости). Следовательно, подтверждается, что найденные значения хорошо согласуются с генетической гипотезой и с предположением о случайном скрещивании для системы ABO.

Позже Бернштейн показал, каким образом разность D можно использовать для коррекции вычисленных частот аллелей. Если обозначить непоправленные частоты p′, q′ и r′, то можно применить следующие формулы:

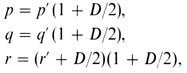
что в нашем случае дает

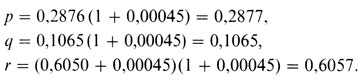
В процессе тестирования двух гипотез о наследовании групп крови ABO Бернштейн разработал методы вычисления частот аллелей. Эти методы приобрели практическое значение и будут подробно рассмотрены нами отдельно (приложение!).

Значение равновесия Харди - Вайнберга. Если наблюдаемые доли генотипов в популяции соответствуют ожидаемым из закона Харди - Вайнберга, то говорят, что популяция находится в равновесии Харди - Вайнберга. Такое равновесие следует отличать от равновесия между аллелями, которое будет рассматриваться при обсуждении отбора (разд. 6.2.1) и мутаций (разд. 5.1.3). Равновесие Харди - Вайнберга - это равновесие распределения генов в популяции (пула генов) между разными генотипами. Если равновесие было нарушено какими-либо силами, то при случайном скрещивании оно восстановится за одно поколение. Следует помнить, однако, что закон Харди - Вайнберга справедлив при следующих условиях.

1. Скрещивания в отношении изучаемых фенотипов должны быть случайными. Это условие можно уверенно считать выполняющимся для таких признаков, как группа крови или полиморфные ферменты. Но вряд ли оно справедливо для морфологических признаков, таких, как рост, а тем более для поведенческих, таких, как интеллект. Об этом необходимо помнить, когда используемые в количественной генетике меры сходства, например корреляции между родственниками, интерпретируются в генетических терминах.
2. Отклонение от случайного скрещивания может быть вызвано, в частности, кровнородственными браками: если в популяции высокий уровень кровного родства, то следует ожидать увеличения количества гомозигот (разд. 6.3.1). Можно даже вычислить частоту кровнородственных браков в популяции на основе отклонений от соотношений Харди - Вайнберга.
3. Соотношения Харди - Вайнберга могут быть нарушены недавними миграциями.
4. Иногда в качестве фактора, нарушающего соотношение Харди - Вайнберга, упоминается отбор. Это справедливо, но не обязательно. Как правило, отбор изменяет генные частоты. Однако отбор, действующий до репродуктивного возраста, например в пренатальном периоде или позже, включая детство и юность, совсем не влияет на соотношения Харди - Вайнберга у взрослых. Отклонения могут наблюдаться в субпопуляции детей в зависимости от конкретного типа отбора. Кроме того, даже при сильном отборе в соответствующей возрастной группе регистрация статистически значимых отклонений от соотношений Харди - Вайнберга требует выборок большого объема - больше, чем обычно имеется в распоряжении исследователя. Иногда вывод об отсутствии значимого отбора формулируется исходя из наблюдаемого соответствия популяции соотношениям Харди - Вайнберга. Однако такой вывод, если он тщательно не проверен, легко может оказаться ошибочным. Рассматривая все теоретические возможности нарушения соотношений, поражаешься тому, как часто в человеческих популяциях, выполняется соотношение Харди - Вайнберга.
5. Формально отклонение от закона Харди - Вайнберга может наблюдаться в том случае, если популяция представляет собой смесь субпопуляций, лишь частично скрещивающихся между собой (случайное скрещивание происходит только внутри субпопуляций, и, следовательно, генные частоты в этих субпопуляциях различны). Впервые на это указал Валунд (1928) [929], который вывел формулу для вычисления коэффициента инбридинга F на основе дисперсий генных частот между субпопуляциями.
6. Другой причиной отклонения может служить существование пока не выявленного ("немого") аллеля, в связи с чем гетерозиготные носители этого аллеля неотличимы от гомозигот по обычному аллелю. Однако Смит (1970) [879] указал, что генетически немой аллель может вызывать значимое отклонение от закона Харди - Вайнберга только тогда, когда гомозиготы по этому аллелю имеют частоту, достаточно высокую, чтобы быть выявленными.